我们将在本文中衡量交易策略的表现。并将开发一个简单的动量交易策略,它将使用四种资产类别:债券、股票和房地产。这些资产类别的相关性很低,这使得它们成为了极佳的风险平衡选择。
动量交易策略
这个策略是基于动量的的,因为交易者和投资者早就意识到动量的影响,这可以在广泛的市场和时间框架中看到。所以我们称之为动量策略。趋势跟踪或时间序列动量 (TSM) 是在单一工具上使用这些策略的另一个名称。我们将创建一个基本的动量策略并在 TCS 上对其进行测试以查看其性能。
TSM策略分析
首先,我们将导入一些库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import yfinance as yf
import ffn
%matplotlib inline
我们构建基本的动量策略函数TSMStrategy。函数将通过时间序列的对数回报、感兴趣的时间段以及是否允许做空的布尔变量的布尔变量来返回预期表现。
def TSMStrategy(returns, period=1, shorts=False):
if shorts:
position = returns.rolling(period).mean().map(
lambda x: -1 if x <= 0 else 1)
else:
position = returns.rolling(period).mean().map(
lambda x: 0 if x <= 0 else 1)
performance = position.shift(1) * returns
return performance
ticker = 'TCS'
yftcs = yf.Ticker(ticker)
data = yftcs.history(start='2005-01-01', end='2021-12-31')
returns = np.log(data['Close'] / data['Close'].shift(1)).dropna()
performance = TSMStrategy(returns, period=1, shorts=False).dropna()
years = (performance.index.max() - performance.index.min()).days / 365
perf_cum = np.exp(performance.cumsum())
tot = perf_cum[-1] - 1
ann = perf_cum[-1] ** (1 / years) - 1
vol = performance.std() * np.sqrt(252)
rfr = 0.02
sharpe = (ann - rfr) / vol
print(f"1-day TSM Strategy yields:" +
f"\n\t{tot*100:.2f}% total returns" +
f"\n\t{ann*100:.2f}% annual returns" +
f"\n\t{sharpe:.2f} Sharpe Ratio")
tcs_ret = np.exp(returns.cumsum())
b_tot = tcs_ret[-1] - 1
b_ann = tcs_ret[-1] ** (1 / years) - 1
b_vol = returns.std() * np.sqrt(252)
b_sharpe = (b_ann - rfr) / b_vol
print(f"Baseline Buy-and-Hold Strategy yields:" +
f"\n\t{b_tot*100:.2f}% total returns" +
f"\n\t{b_ann*100:.2f}% annual returns" +
f"\n\t{b_sharpe:.2f} Sharpe Ratio")
函数输出如下:
1-day TSM Strategy yields:
-45.15% total returns
-7.10% annual returns
-0.17 Sharpe Ratio
Baseline Buy-and-Hold Strategy yields:
-70.15% total returns
-13.78% annual returns
-0.22 Sharpe Ratio
在合理的年化回报上,1日TSM策略优于买入并持有策略。因为 1 天的回顾可能包含许多错误趋势,所以我们尝试不同的时间段来查看它们的比较情况。这里将循环运行模型 3、5、15、30 和 90 天。
import matplotlib.gridspec as gridspec
periods = [3, 5, 15, 30, 90]
fig = plt.figure(figsize=(12, 10))
gs = fig.add_gridspec(4, 4)
ax0 = fig.add_subplot(gs[:2, :4])
ax1 = fig.add_subplot(gs[2:, :2])
ax2 = fig.add_subplot(gs[2:, 2:])
ax0.plot((np.exp(returns.cumsum()) - 1) * 100, label=ticker, linestyle='-')
perf_dict = {'tot_ret': {'buy_and_hold': (np.exp(returns.sum()) - 1)}}
perf_dict['ann_ret'] = {'buy_and_hold': b_ann}
perf_dict['sharpe'] = {'buy_and_hold': b_sharpe}
for p in periods:
log_perf = TSMStrategy(returns, period=p, shorts=False)
perf = np.exp(log_perf.cumsum())
perf_dict['tot_ret'][p] = (perf[-1] - 1)
ann = (perf[-1] ** (1/years) - 1)
perf_dict['ann_ret'][p] = ann
vol = log_perf.std() * np.sqrt(252)
perf_dict['sharpe'][p] = (ann - rfr) / vol
ax0.plot((perf - 1) * 100, label=f'{p}-Day Mean')
ax0.set_ylabel('Returns (%)')
ax0.set_xlabel('Date')
ax0.set_title('Cumulative Returns')
ax0.grid()
ax0.legend()
_ = [ax1.bar(i, v * 100) for i, v in enumerate(perf_dict['ann_ret'].values())]
ax1.set_xticks([i for i, k in enumerate(perf_dict['ann_ret'])])
ax1.set_xticklabels([f'{k}-Day Mean'
if type(k) is int else ticker for
k in perf_dict['ann_ret'].keys()],
rotation=45)
ax1.grid()
ax1.set_ylabel('Returns (%)')
ax1.set_xlabel('Strategy')
ax1.set_title('Annual Returns')
_ = [ax2.bar(i, v) for i, v in enumerate(perf_dict['sharpe'].values())]
ax2.set_xticks([i for i, k in enumerate(perf_dict['sharpe'])])
ax2.set_xticklabels([f'{k}-Day Mean'
if type(k) is int else ticker for
k in perf_dict['sharpe'].keys()],
rotation=45)
ax2.grid()
ax2.set_ylabel('Sharpe Ratio')
ax2.set_xlabel('Strategy')
ax2.set_title('Sharpe Ratio')
plt.tight_layout()
plt.show()
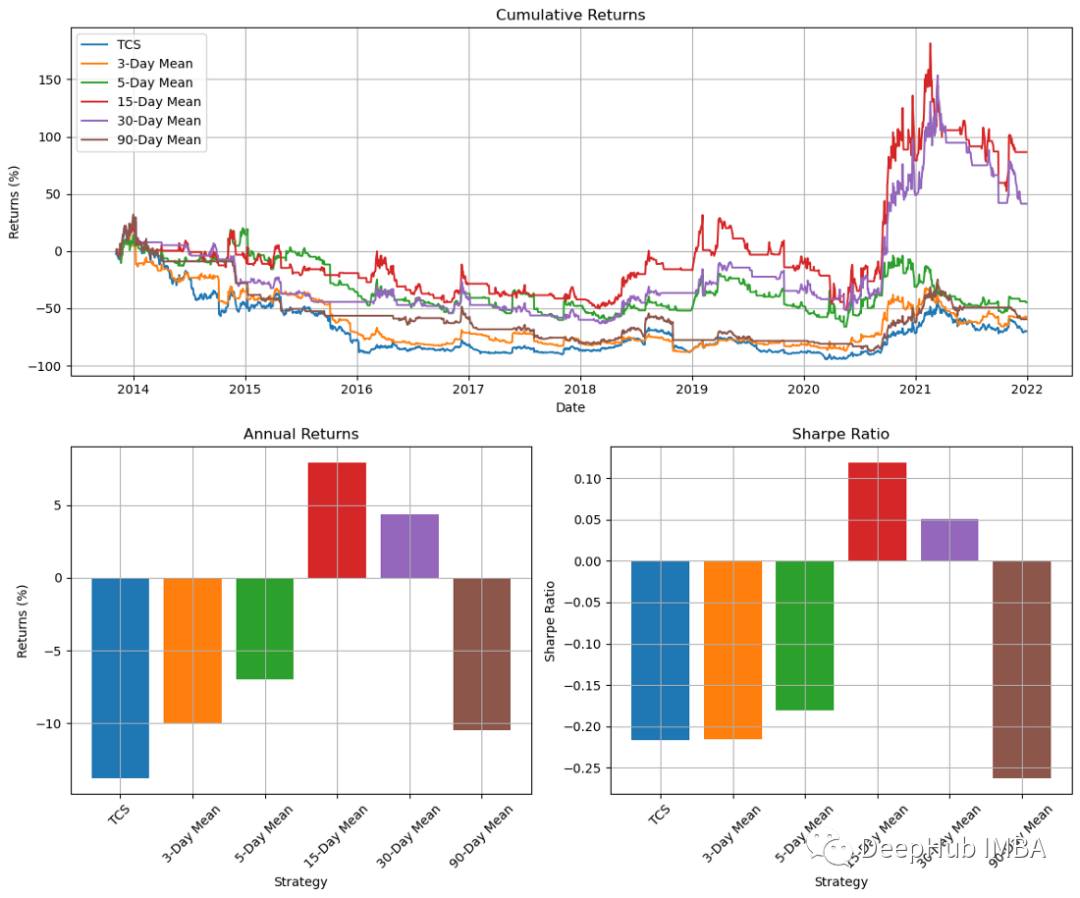
通过图表的结果,我们可以看到15天的动量指标提供了最好的结果。但是,其他时间周期的结果是五花八门的。这表明我们这个策略并不可靠。所以我们还可以通过在接近顶部时使用止损或追踪止损来退出交易,而不是在15日线图下跌或持平时再进行操作。
投资组合分析
到目前为止,我们已经用Python创建了一个交易策略。下面我们将度量并绘制常见的投资组合特征方便我们进行观察分析。
投资组合分析
首先,我们将导入一些重要的库,并观察数据执行情况。
import pandas_datareader.data as web
stocks = ['SPY','GLD','TLT','HYG']
data = web.DataReader(stocks,data_source='yahoo',start='01/01/2019')['Adj Close']
data.sort_index(ascending=True,inplace=True)
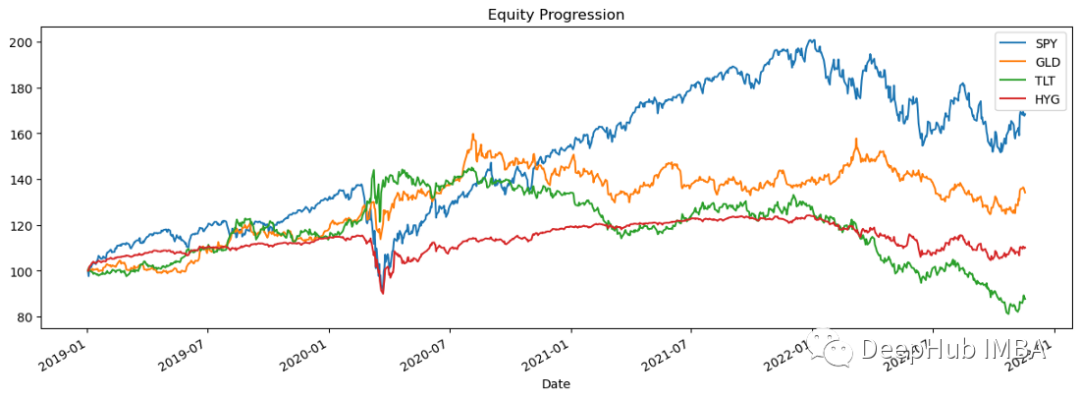
perf = data.calc_stats()
perf.plot()
对数回报
对数回报用于计算指数增长率。我们不计算每个子时期的价格变化百分比,而是计算那段时间的自然增长指数。首先创建一个df,其中包含数据中每个股票价格的对数回报,然后我们为每个对数回报创建一个直方图。
returns = data.to_log_returns().dropna()
print(returns.head())
Symbols SPY GLD TLT HYG
Date
2019-01-03 -0.024152 0.009025 0.011315 0.000494
2019-01-04 0.032947 -0.008119 -0.011642 0.016644
2019-01-07 0.007854 0.003453 -0.002953 0.009663
2019-01-08 0.009351 -0.002712 -0.002631 0.006470
2019-01-09 0.004663 0.006398 -0.001566 0.001193
直方图如下:
ax = returns.hist(figsize=(20, 10),bins=30)
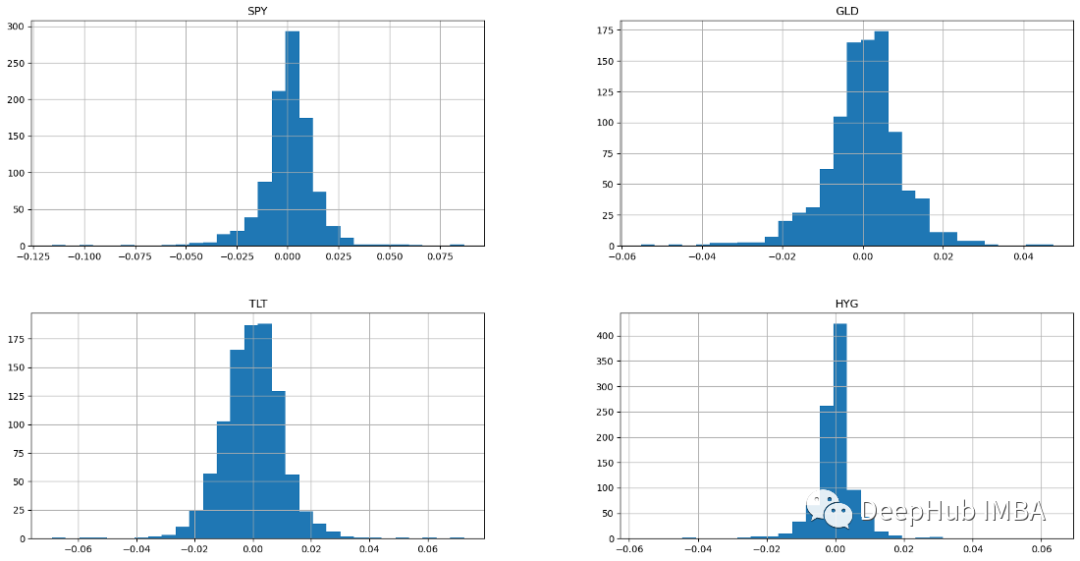
所有四个资产类别都显示正态分布的直方图。具有正态分布的样本具有算术平均值和高于和低于平均值的均等分布(正态分布也称为高斯分布是对称的) 。如果回报呈正态分布,预计超过 99% 的回报将落在平均值的三个标准差范围内。这些钟形正态分布特征使分析师和投资者能够对股票的预期收益和风险进行更好的统计推断。具有钟形曲线的股票通常是波动率低且可预测的蓝筹股(Blue Chips)。
最大回撤率 DRAWDOWN
DRAWDOWN是指价值下降到一个相对的低谷。这是投资者需要考虑的一个重要风险因素。让我们画一个递减策略的可视化表示。
ffn.to_drawdown_series(data).plot(figsize=(15,10))
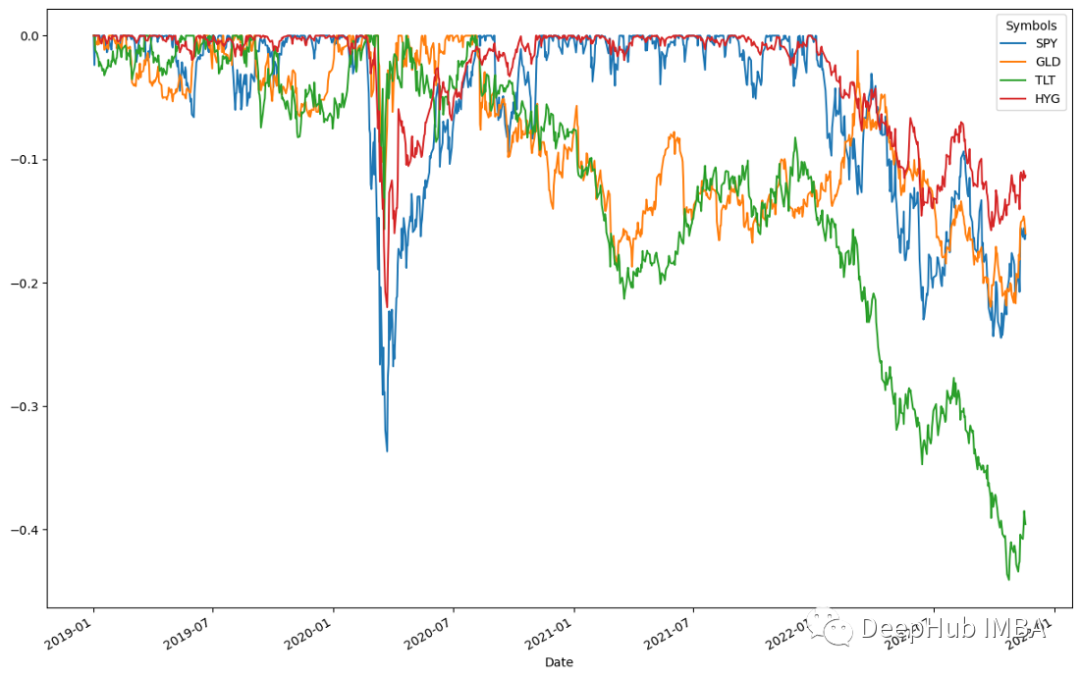
这四种资产在2020年上半年都出现了下降,其中SPY的降幅最大,为0.5%。随后,在2020年上半年,所有资产立即复苏。这表明资产回收率很高。这些资产在2020年7月前后见顶。按照这种趋势,一旦复苏达到顶峰,所有资产类别都出现小幅下跌。根据结果TLT将在2022年下半年经历最大的0.5%的下降,然后在2023年初之前恢复。
MARKOWITZ 均值-方差优化
1952年,马科维茨(MARKOWITZ)提出均值-方差投资组合理论,又称现代投资组合理论。投资者可以使用这些概念来构建基于给定风险水平的最大化预期回报的投资组合。基于马科维茨方法,我们可以生成“最优投资组合”。
returns.calc_mean_var_weights().as_format('.2%')
#结果
SPY 46.60%
GLD 53.40%
TLT 0.00%
HYG 0.00%
dtype: object
相关性统计
相关性是一种统计方法,用来衡量证券之间的相互关系。最好使用热图来查看这些信息。热图可以让我们看到证券之间的相关性。
returns.plot_corr_heatmap()
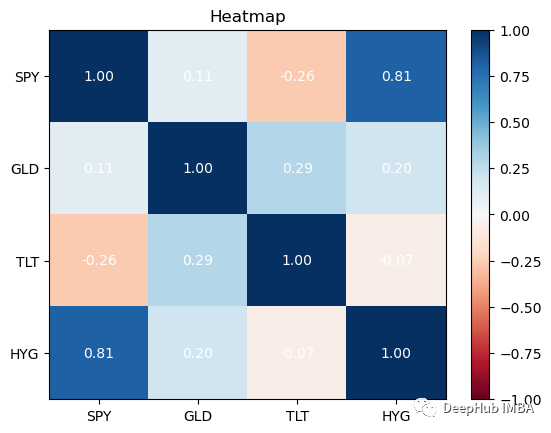
最好在你的投资组合中拥有相关性较低的资产。除了SPY与HYG,这四个资产类别的相关性都很低,这对我们的投资组合是不利的:因为如果拥有高度相关的不同资产组,即使你将风险分散在它们之间,从投资组合构建的角度来看,收益也会很少。
总结
通过分析和绘制的所有数据进行资产配置,可以建立一个投资组合,极大地改变基础投资的风险特征。还有很多我没有提到的,但可以帮助我们确定交易策略价值的起点。我们将在后续文章中添加更多的技术性能指标。
本文的代码:
https://avoid.overfit.cn/post/e0dda8fc7ce245349db4ddb55ee491ba
作者:Mpho Lukhele






![[附源码]Python计算机毕业设计电子工厂进销存管理系统](https://img-blog.csdnimg.cn/7e12547693b945d4af1fe0d6525e3aa4.png)