目录
- 1.积木画
- 1.题目描述
- 2.输入格式
- 3.输出格式
- 4.样例输入
- 5.样例输出
- 6.样例说明
- 7.数据范围
- 8.原题链接
- 2.解题思路
- AC_code
1.积木画
1.题目描述
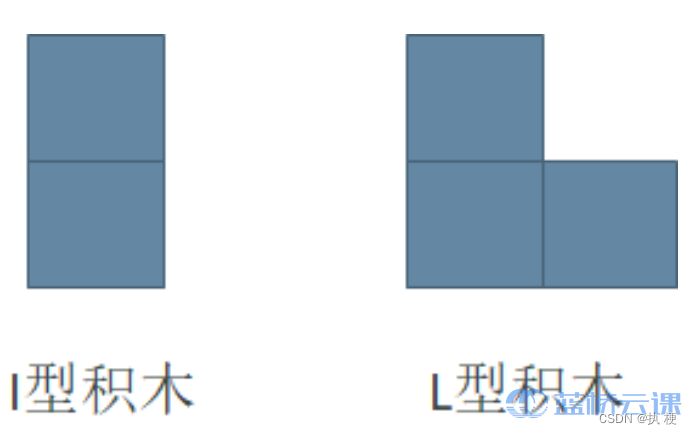
小明最近迷上了积木画, 有这么两种类型的积木, 分别为
I
I
I 型(大小为 2 个单位面积) 和
L
L
L 型 (大小为 3 个单位面积):
同时, 小明有一块面积大小为
2
×
N
2 \times N
2×N 的画布, 画布由
2
×
N
2 \times N
2×N 个
1
×
1
1 \times 1
1×1 区域构 成。小明需要用以上两种积木将画布拼满, 他想知道总共有多少种不同的方式? 积木可以任意旋转, 且画布的方向固定。
2.输入格式
输入一个整数 N N N,表示画布大小。
3.输出格式
输出一个整数表示答案。由于答案可能很大,所以输出其对 1000000007 取模后的值。
4.样例输入
3
5.样例输出
5
6.样例说明
五种情况如下图所示,颜色只是为了标识不同的积木:
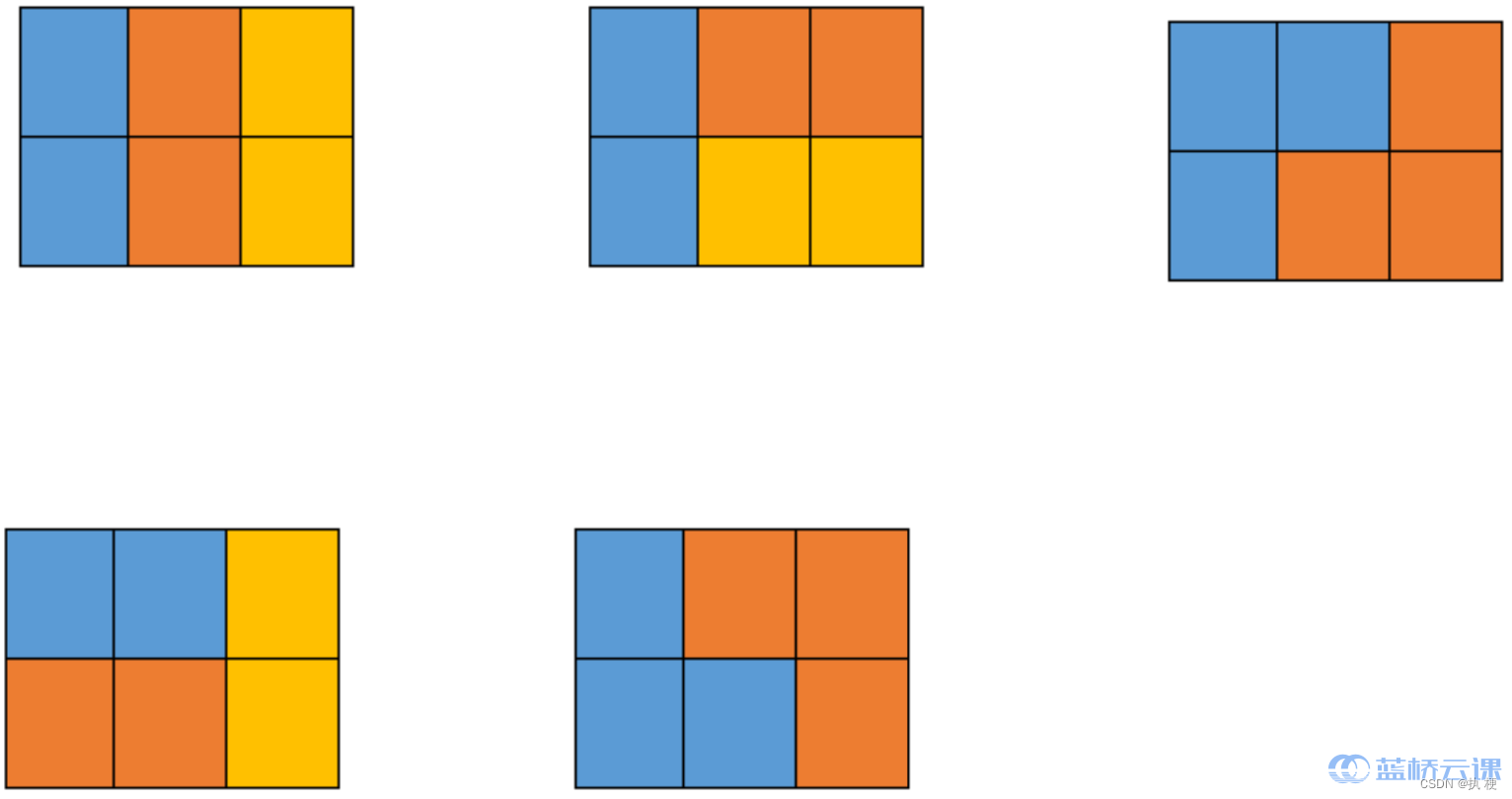
7.数据范围
1 ≤ N ≤ 1 0 7 1≤N≤10^7 1≤N≤107
8.原题链接
积木画
2.解题思路
比较简单的状态压缩
d
p
dp
dp 的模型,虽然
N
N
N 很大,但总共只有两行,所以只需要考虑结尾的插入情况即可。
定义
f
[
i
]
[
j
]
f[i][j]
f[i][j] 为已经排好了前
i
−
1
i-1
i−1 列,且第
i
i
i 列的状态为
j
j
j 的方案数。当
j
j
j 为 0 时表示第
i
i
i 列上面和下面均未摆放积。为 1 时表示上面未摆,下面摆放了积木。当为 2 时表示上面摆了,下面未摆的情况,当为 3 时表示上下均摆好了积木的情况。
从定义可知最终答案为
f
[
n
]
[
3
]
f[n][3]
f[n][3]
考虑如何进行初始化,当
n
n
n 为0时,可以视为完全摆好的情况,则
f
[
0
]
[
3
]
=
1
f[0][3]=1
f[0][3]=1,当
n
n
n 为 1 时,只有一种摆法,则
f
[
1
]
[
3
]
=
1
f[1][3]=1
f[1][3]=1。
接下来考虑如何进行状态转移:
首先考虑
f
[
i
]
[
0
]
f[i][0]
f[i][0] ,因为0表示上下都未摆放积木,而状态定义就要求了前
i
−
1
i-1
i−1列已经摆好,则转移方程:
f
[
i
]
[
0
]
=
f
[
i
−
1
]
[
3
]
f[i][0]=f[i-1][3]
f[i][0]=f[i−1][3]
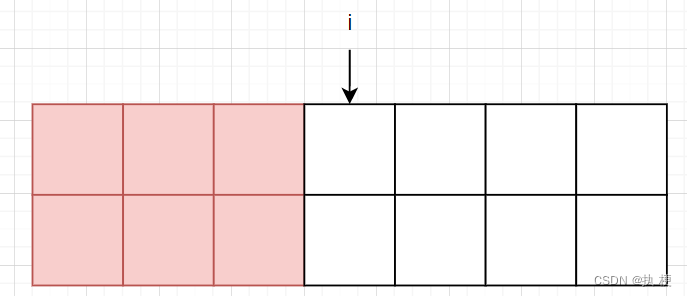
然后考虑 f [ i − 1 ] [ 1 ] f[i-1][1] f[i−1][1]如何转移:
1表示我们第
i
i
i 列是下面摆放了上面未摆放,也就是下面突出了一格,我们考虑如何才会产生这样的效果:
当这样摆放时可以得到,但转移时不应该从
i
−
1
i-1
i−1 列转移,而应该是从
f
[
i
−
2
]
[
3
]
f[i-2][3]
f[i−2][3] 转移。
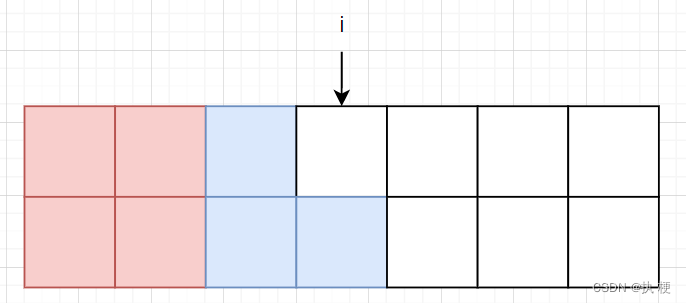
除此之外我们还可以像下面这样插入,这样我们可以从
f
[
i
−
1
]
[
2
]
f[i-1][2]
f[i−1][2]转移过来。
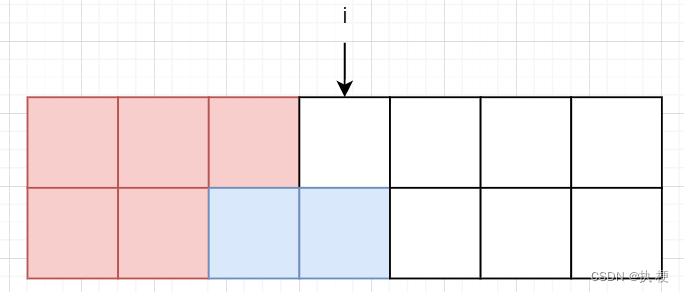
综上我们有两种情况可以得到
f
[
i
]
[
1
]
f[i][1]
f[i][1],转移方程为:
f
[
i
]
[
1
]
=
(
f
[
i
−
1
]
[
0
]
+
f
[
i
−
1
]
[
2
]
)
f[i][1] = (f[i - 1][0] + f[i - 1][2])
f[i][1]=(f[i−1][0]+f[i−1][2])
分析
f
[
i
]
[
2
]
f[i][2]
f[i][2]其实和
f
[
i
]
[
1
]
f[i][1]
f[i][1]同理,反过来就行,有如下两种插入情况:
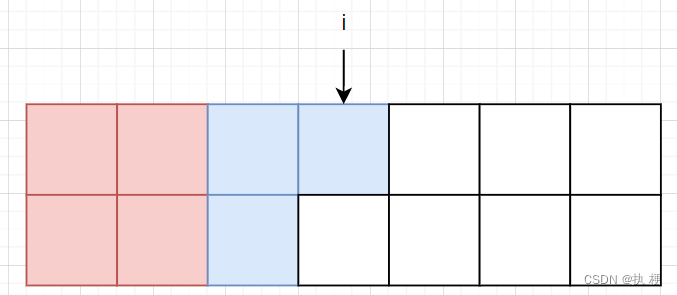
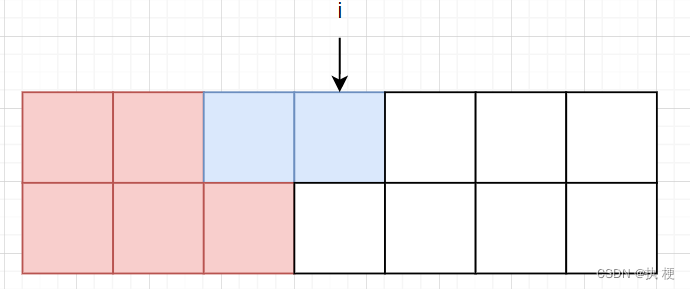
那么转移方程则为:
f
[
i
]
[
2
]
=
(
f
[
i
−
1
]
[
0
]
+
f
[
i
−
1
]
[
1
]
)
f[i][2] = (f[i - 1][0] + f[i - 1][1])
f[i][2]=(f[i−1][0]+f[i−1][1])
最后考虑
f
[
i
]
[
3
]
f[i][3]
f[i][3]如何转移,这个转移的情况比较多,直接上图大家就能看懂了:
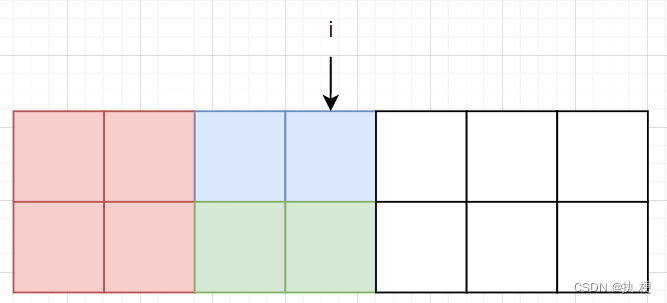
横着插两块,从
f
[
i
−
2
]
[
3
]
f[i-2][3]
f[i−2][3]转移
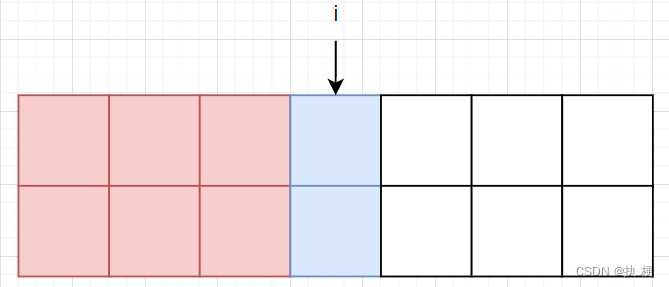
可以从
f
[
i
−
1
]
[
3
]
f[i-1][3]
f[i−1][3]转移
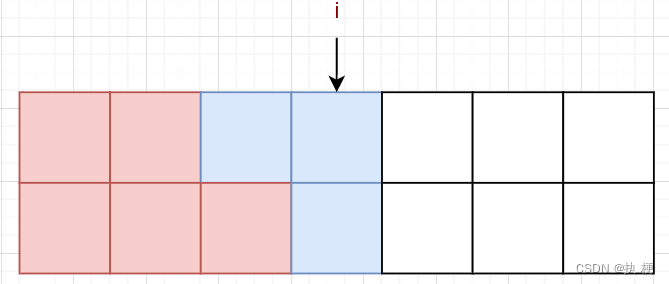
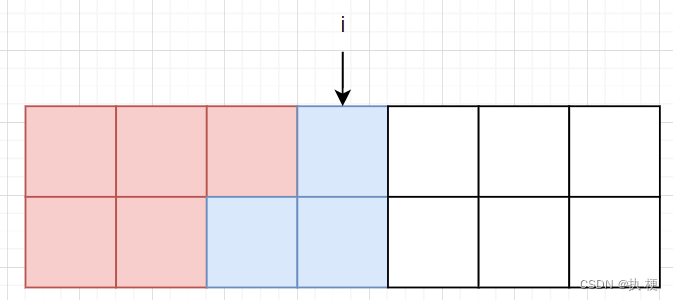
可以从
f
[
i
−
1
]
[
1
]
f[i-1][1]
f[i−1][1]和
f
[
i
−
1
]
[
2
]
f[i-1][2]
f[i−1][2]转移,综上:
f
[
i
]
[
3
]
=
(
f
[
i
−
2
]
[
3
]
+
f
[
i
−
1
]
[
3
]
+
f
[
i
−
1
]
[
2
]
+
f
[
i
−
1
]
[
1
]
)
f[i][3] = (f[i - 2][3] + f[i - 1][3] + f[i - 1][2] + f[i - 1][1])
f[i][3]=(f[i−2][3]+f[i−1][3]+f[i−1][2]+f[i−1][1])
AC_code
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 10000010;
int n;
// f[i][j]表示已经操作完前i-1列,且第i列的状态为j的方案数
LL f[N][3];
void solve()
{
cin >> n;
f[0][3] = 1;
f[1][3] = 1;
for (int i = 2; i <= n; ++i) {
f[i][0] = f[i - 1][3];
f[i][1] = (f[i - 1][0] + f[i - 1][2]) % mod;
f[i][2] = (f[i - 1][0] + f[i - 1][1]) % mod;
f[i][3] = (f[i - 2][3] + f[i - 1][3] + f[i - 1][2] + f[i - 1][1]) % mod;
}
cout << f[n][3] << '\n';
}
int main()
{
ios_base :: sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
while (t--)
{
solve();
}
return 0;
}








![[附源码]SSM计算机毕业设计农贸产品交易系统JAVA](https://img-blog.csdnimg.cn/086fe818ee974edebeb8a76727bac994.png)



![[HFCTF2020]EasyLogin](https://img-blog.csdnimg.cn/814b34c17b02417ea72dc7566afada18.png)