引入

1.什么是动态规划?

动态规划（英语：Dynamic programming，简称 DP），是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。
核心思想: 通过将问题拆分成一个一个小问题，记录过往结果，减少重复运算。

举个栗子：

A ： "1+1+1+1+1+1+1+1 =？"
A ： "上面等式的值是多少"
B ：计算 "8"
A : 在上面等式的左边写上 "1+" 呢？
A : "此时等式的值为多少"
B : 很快得出答案 "9"
A : "你怎么这么快就知道答案了"
A : "只要在8的基础上加1就行了"
A : "所以你不用重新计算，因为你记住了第一个等式的值为8!动态规划算法也可以说是 '记住求过的解来节省时间'"

感谢🙇‍

@四舍五入两米高的小晨

2.什么是背包问题？

背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。相似问题经常出现在商业、组合数学，计算复杂性理论、密码学和应用数学等领域中。也可以将背包问题描述为决定性问题，即在总重量不超过W的前提下，总价值是否能达到V？它是在1978年由Merkle和Hellman提出的。

常见分类：

01背包
完全背包
多重背包
分组背包

3.什么是01背包？

01背包是背包问题中最简单的问题。01背包的约束条件是给定几种物品，每种物品有且只有一个，并且有权值和体积两个属性。在01背包问题中，因为每种物品只有一个，对于每个物品只需要考虑选与不选（0与1）两种情况。如果不选择将其放入背包中，则不需要处理。如果选择将其放入背包中，由于不清楚之前放入的物品占据了多大的空间，需要枚举将这个物品放入背包后可能占据背包空间的所有情况。

对于这类问题，可采用深搜+剪枝或动态规划的方法，今天我们用动规来AC此题。

模板题

1.题面

这类问题的模板题，有一道十分经典，它是：[NOIP2005 普及组] 采药

【NOIP2005 普及组】采药

题目描述：
辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

输入格式：
第一行有 22 个整数 TT（1 \le T \le 10001≤T≤1000）和 MM（1 \le M \le 1001≤M≤100），用一个空格隔开，TT 代表总共能够用来采药的时间，MM 代表山洞里的草药的数目。

接下来的 MM 行每行包括两个在 11 到 100100 之间（包括 11 和 100100）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式：
输出在规定的时间内可以采到的草药的最大总价值。

输入输出样例
输入：

70 3
71 100
69 1
1 2
输出：

3

这道题，就是将原始题目换了个故事。原始题：

有一个容量为V的背包，还有n个物体。现在忽略物体实际几何形状，我们认为只要背包的剩余容量大于等于物体体积，那就可以装进背包里。每个物体都有两个属性，即体积w和价值v。
问：如何向背包装物体才能使背包中物体的总价值最大？

2.思路

Ⅰ为何不可用贪心

很多人看到此题第一个反应便是贪心。但为什么这个问题不能用贪心呢？

举个栗子：
我的背包容量为10，而且有4个物体，它们的体积和价值分别为
w1 = 8, v1 = 9
w2 = 3, v2 = 3
w3 = 4, v3 = 4
w4 = 3, v4 = 3
贪心是每一步采取最优拿法，即每一次都优先拿价值与体积比值最大的物体
c1 = v1/w1 = 1.125（最大）
c2 = v2/w2 = 1
c3 = v3/w3 = 1
c4 = v4/w4 = 1
所以优先拿第一个物体，随后背包再也装不下其他物体了，则最大价值为9。
但是这个问题的最优解是取物体2，3，4装进背包，最大价值为3+4+3=10！（9<10)
感谢🙇‍@Iseno_V

所以这个问题不可以用贪心法来处理。

Ⅱ状态转移方程

先设wi表示第i个物品的重量，vi表示第i个物品的价值。

动态规划的核心是状态转移方程。可以发现：最大价值是物品数量i和背包容量j的函数。

设函数f[i][j]表示前i件物品放入容量为j的背包的最大价值，
最终的最大价值就是物品数量i从0增长到n，背包容量j从0增长到m时的f[n][m]值。

前面说了，01背包对于每个物品只需要考虑选与不选（0与1）两种情况。当前容量为j，我们要考虑第i件物品能否放入？是否放入？

①如果当前背包容量j<v[i],不能放入，则f[i][j]=f[i-1][j]

②如果当前背包容量j>=v[i]，能放入但是要比较代价，看放入价值高还是不放入价值高。
2.1 如果第i件物品不放入背包，则f[i][j]=f[i-1][j]
2.2 如果第i件物品放入背包，则f[i][j]=f[i-1][j-w[i]]+v[i]
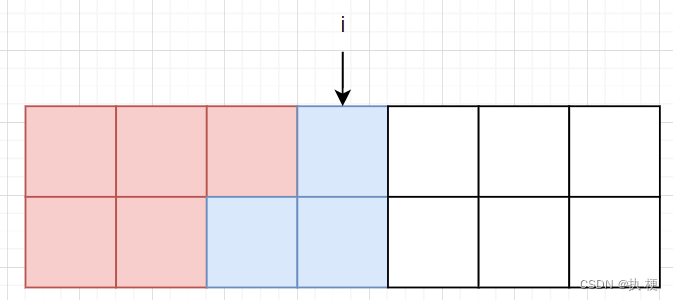
如果第i件物品放入背包，则背包容量还剩j-w[i],所以要取前i-1件物品放入背包剩余容量j-w[i]所获得的最大价值f[i-1][j-w[i]]。如图：

正在上传…

重新上传

因此，得到状态转移方程：

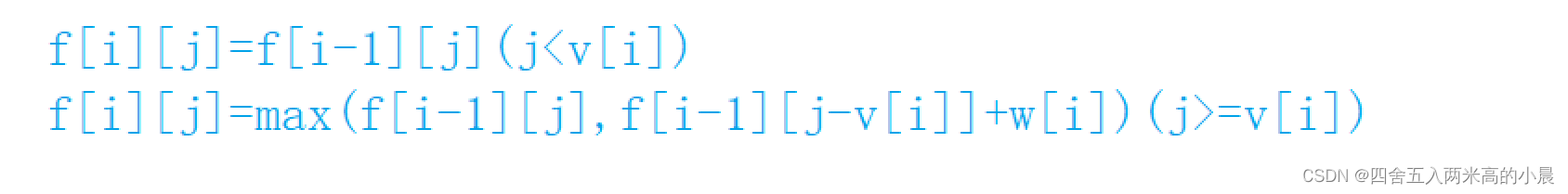
3.代码

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1010;
int n,m;
int v[N],w[N];//v数组存储体积，w数组存储价值
int f[N][N];
int main ()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++)
            {
                f[i][j]=f[i-1][j];//将不能放入第i件物品的情况和能放入但是没放入的情况合并
                if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
            }
    cout<<f[n][m]<<endl;
    return 0;
}