1.背景

PD（Projective Dynamics）仿真算法是一种“可并行化计算的”高效的软体形变模拟（或成为仿真、动画）算法，与传统的基于力的有限元方法不同的是，PD算法直接作用于顶点位置，通过最小化能量函数的方式来求得一个稳定的解。能量函数一般包括“系统偏离预期位置的能量”和“顶点位置约束能量”两部分组成，最小化能量函数可以通过引入辅助变量的方法转换为求解一个线性方程组的问题。详细的PD算法不在这里展开。

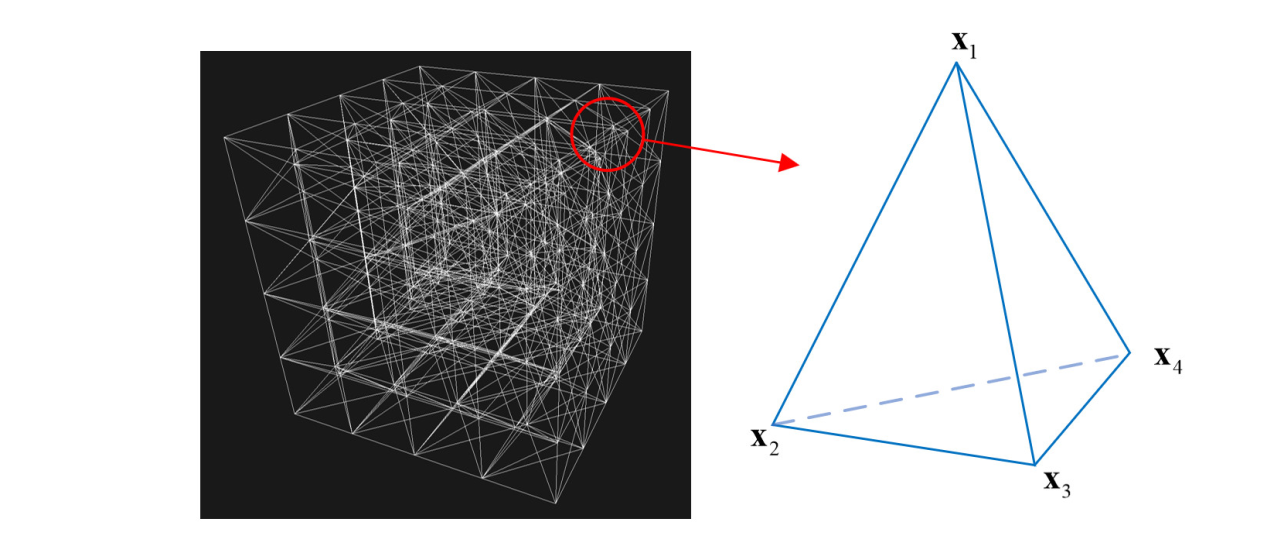
本文要讨论的是PD算法中对于四面体网格模型“形状约束”的求解中矩阵论知识的应用。

四面体网格模型的“元”为四个顶点组成的四面体 { x 1 , x 2 , x 3 , x 4 } \{\mathbf{x}_1,\mathbf{x}_2,\mathbf{x}_3,\mathbf{x}_4\} {x1​,x2​,x3​,x4​}，我们定义其形状
$$\mathbf{X}=[{\mathbf{x}}_2-{\mathbf{x}}_1,{\mathbf{x}}_3-{\mathbf{x}}_1,{\mathbf{x}}_4-{\mathbf{x}}_1],\text{\hspace{1em}(1.1)}$$
定义形状的方式可能有很多，但是需要与空间位置无关，也就是要满足平移不变性。假设初始形状为“非奇异的”${\mathbf{X}}_0$，那么对于变形之后的四面体形状$\mathbf{X}$，有
$$\mathbf{X}=\mathbf{F}{\mathbf{X}}_0\text{或}\mathbf{F}=\mathbf{X}{\mathbf{X}}_0^{-1},\text{\hspace{1em}(1.2)}$$
其中$\mathbf{F}$就是变形梯度矩阵。在PD算法中对于约束需要导出一个能量项，因此本文探讨的是如何导出变形梯度矩阵的能量函数。

2.极分解

为了对变形梯度矩阵进行“符合物理规律”的分解，首先需要了解极分解（polar decomposition）定理。

定理2.1（极分解）：设$\mathbf{A}$是$n$阶实方阵，则一定存在正交矩阵$\mathbf{Q}$和唯一的半正定矩阵$\mathbf{T}$，使得$\mathbf{A}=\mathbf{Q}\mathbf{T}$。若$\mathbf{A}$可逆，则$\mathbf{Q}$也是唯一的，并且$\mathbf{T}$是正定的。

证明：

存在奇异值分解 $\mathbf{A}=\mathbf{V}\mathbf{S}{\mathbf{U}}^T$，其中$\mathbf{V},\mathbf{U}$是正交阵， S = diag { σ 1 , … , σ r , 0 , … , 0 } \mathbf{S}=\text{diag}\{\sigma_1,\dots,\sigma_r,0,\dots,0\} S=diag{σ1​,…,σr​,0,…,0}，${\sigma }_1\ge \cdots \ge {\sigma }_r>0$，做变换
$$\begin{array}{rl}\mathbf{A}& =\mathbf{V}\mathbf{S}{\mathbf{U}}^T\\ & =\mathbf{V}{\mathbf{U}}^T\mathbf{U}\mathbf{S}{\mathbf{U}}^T\\ & =\mathbf{Q}\mathbf{T},\\ \mathbf{Q}& =\mathbf{V}{\mathbf{U}}^T,\mathbf{T}=\mathbf{U}\mathbf{S}{\mathbf{U}}^T,\end{array}\text{\hspace{1em}(2.1)}$$
则$\mathbf{Q}$是正交矩阵，$\mathbf{T}$是半正定矩阵（特征值不小于0，对称）；注意到
$$\begin{array}{rl}\mathbf{T}& =\mathbf{U}\mathbf{S}{\mathbf{U}}^T\\ & =(\mathbf{U}\mathbf{S}{\mathbf{U}}^T\mathbf{U}\mathbf{S}{\mathbf{U}}^T{)}^{\frac{1}{2}}\\ & =(\mathbf{U}\mathbf{S}\mathbf{S}{\mathbf{U}}^T{)}^{\frac{1}{2}}\\ & =({\mathbf{A}}^T\mathbf{A}{)}^{\frac{1}{2}},\end{array}\text{\hspace{1em}(2.2)}$$
其中${\mathbf{A}}^T\mathbf{A}$是半正定矩阵，有$r=r({\mathbf{A}}^T\mathbf{A})=r(\mathbf{A})$个非零特征值，则其平方根共有$2^r$种可能性，显然对于每个非零特征值都有正负两种平方根（即$\pm {\sigma }_i$）可以选取。而当所有非零特征值都选择正平方根（${\sigma }_i$）时，“半正定矩阵”$\mathbf{T}$就是唯一的。为什么$\mathbf{Q}$不唯一呢？因为$\mathbf{T}$里面有些特征值是$0$。

当$\mathbf{A}$可逆，也就是$\mathbf{A}$的特征值都不为$0$，此时显然$\mathbf{T}$是正定的，也是可逆的，因此$\mathbf{Q}$唯一确定：
$$\mathbf{Q}=\mathbf{A}{\mathbf{T}}^{-1}\text{\hspace{1em}(2.3)}$$

3.变形梯度的分解

回顾变形梯度的定义式1.1，首先规定一点，四面体形状$\mathbf{X}$在任何时候都是“非奇异”的，也就是不会退化成平面的情况。因此，变形梯度是可逆的。

根据定理2.1，可对变形梯度进行极分解：
$$\mathbf{F}=\mathbf{R}\mathbf{S},\text{\hspace{1em}(3.1)}$$
其中$\mathbf{R}$是“唯一的“正交阵，$\mathbf{S}$是”唯一的”正定阵。

这么做的好处是分解后的矩阵将“变形”的旋转部分和其它部分分离开来，$\mathbf{R}$是旋转部分（“rotation”），$\mathbf{S}$是拉伸和切变部分（“stretch"和"shear”）。$|\mathbf{S}|$描述了四面体的体积变化。

具体分解步骤（前面的公式是教材上的公式，这里为了适应NumPy的定义换了符号）：

1. 奇异值分解：$\mathbf{F}=\mathbf{U}\mathbf{S}\mathbf{V}$；
2. 计算 $\mathbf{R}=\mathbf{U}\mathbf{V}$ 和 $\mathbf{S}={\mathbf{V}}^T\mathbf{S}\mathbf{V}$ 。

4.实验

为了可视化地验证变形梯度矩阵的极分解，我设计了一个小实验：固定四面体的顶点${\mathbf{x}}_1=(0,0,0{)}^T$，变形前后的形状矩阵设置为
$$\begin{array}{r}{\mathbf{X}}_1=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right],{\mathbf{X}}_2=\left[\begin{array}{ccc}-0.5& -1.3& 0\\ 1.5& 0& 0\\ 0& 0& 2.3\end{array}\right],\end{array}\text{\hspace{1em}(4.1)}$$

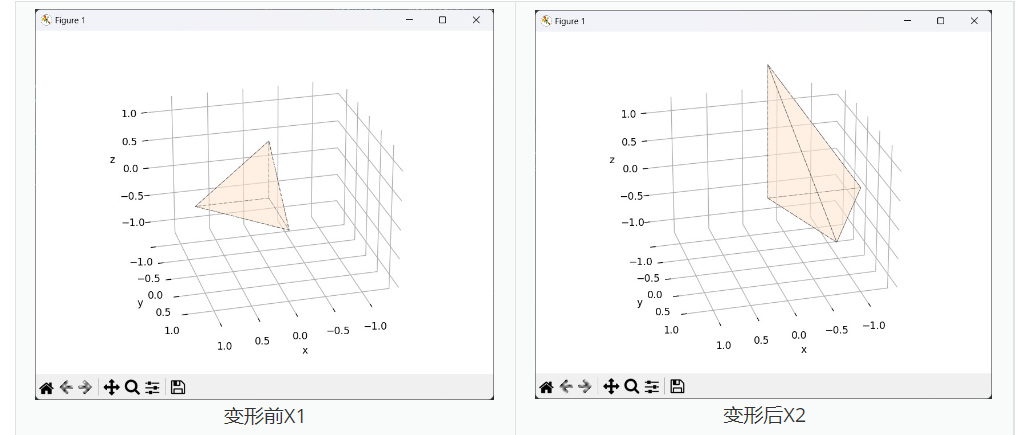
直观上来看上述变形就是将四面体绕$z$轴旋转90°，并且每个轴的方向拉伸一个系数，然后把${\mathbf{x}}_2$沿$x$轴移动$-0.5$。

根据第3节讲的变形梯度矩阵极分解的步骤，得到的结果为
$$\begin{array}{rl}& \mathbf{R}=\left[\begin{array}{ccc}-0.17579064& -0.98442758& 0\\ 0.98442758& -0.17579064& 0\\ 0& 0& 1\end{array}\right],\mathbf{S}=\left[\begin{array}{ccc}1.56453668& 0.22852783& 0\\ 0.22852783& 1.27975585& 0\\ 0& 0& 2.3\end{array}\right],\\ & |\mathbf{R}|=1,|\mathbf{S}|=4.485,\end{array}\text{\hspace{1em}(4.2)}$$
单独对初始形状${\mathbf{X}}_1$应用$\mathbf{R}$和$\mathbf{S}$的结果如下：

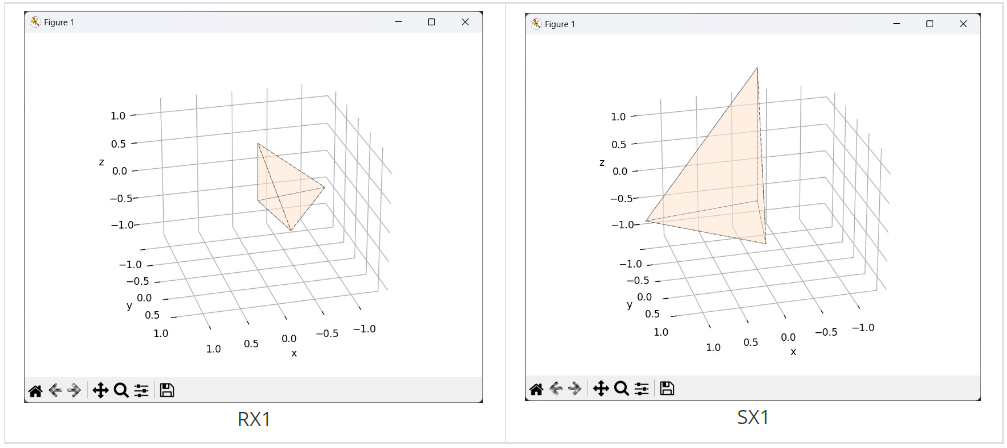
实验结果符合预期。