给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
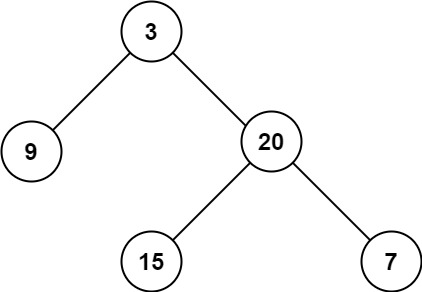
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
提示:
- 树中节点的数量在
[0, 104]区间内。 -100 <= Node.val <= 100
思路: //一层一层去遍历,将根节点先存入队列,深度+1,然后判断如果有左子树或者右子树不为空则将其存入队列,深度+1,根节点再出队列,第二次还是遍历这个队列就是将根节点的左子树判断这个的左子树和右子树以及根节点的右子树判断这个的左子树和右子树(队列中有就执行),就是每层节点找下面层所有节点,并将该层节点退队列,下面层所有节点存入队列,直到队列中没节点了,就结束
代码:C#
public class Solution {
public int MaxDepth(TreeNode root) {
if(root==null)
return 0;
Queue<TreeNode> queue=new Queue<TreeNode>();//创建一个队列
int depth=0;//深度为0
queue.Enqueue(root);//将根节点存入队列
while(queue.Count>0)//循环结束条件为队列中节点数量小于等于0
{
depth++;//只要进入该循环一次深度就+1
int len=queue.Count;//这里需要int出队列长度
for(int i=0;i<len;i++)//不能不int len,直接写queue.Count,因为i增加循环中队列大小在减小,容易出现有队列没遍历完全的情况
{
TreeNode newnode=queue.Dequeue();
if(newnode.left!=null)
{
queue.Enqueue(newnode.left);
}
if(newnode.right!=null)
{
queue.Enqueue(newnode.right);
}
}
}
return depth;
}
}



















