790. 多米诺和托米诺平铺 - 力扣（LeetCode）

题目

有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 "L" 的托米诺形。两种形状都可以旋转。

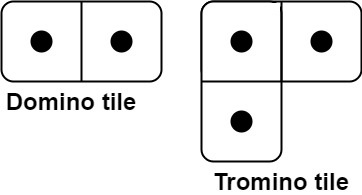
给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。

平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

示例 1:

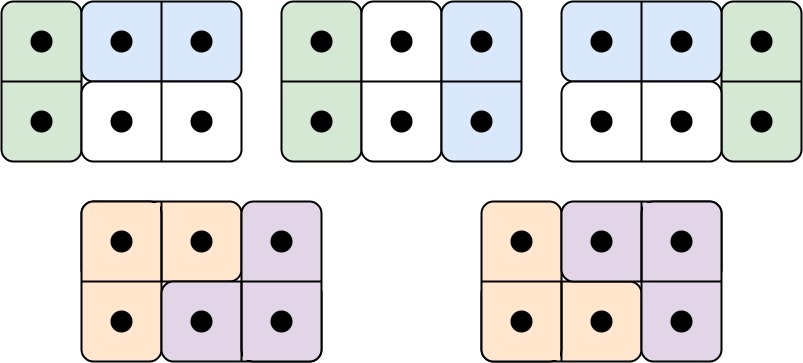
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。

示例 2:

输入: n = 1
输出: 1

提示：

• 1 <= n <= 1000

思路（纯脑洞，没实现）

1. 这题看起来是个排列组合题，先从全铺domino的情况开始，逐渐减少domino再看是否能加上tromino。
2. 确定完最外层的逻辑考虑哪些组合能铺满，再考虑每个组合怎么铺：
   1. 首先是domino和domino的组合，一般只能横着或竖着铺：
      1. 横着下面必然也得需要一个domino，所以消耗2个domino，占4格，因为对称性，所以只有1种组合方式；
      2. 竖着可以单独组合，消耗1个domino，占2格，1种组合方式。
   2. 然后是tromino和tromino的组合，只能交叉嵌入，消耗2个tromino，占6格，有2种组合方式。
   3. 最后是domino和tromino的组合，只能是两个对称的tromino夹着一个domino，消耗2个tromino和1个domino，占8格，有两种组合方式。
3. 根据上述情况，这个问题就变成了怎么解有重复元素的排列问题（好吧怎么把组合罗列出来也挺麻烦的）。

官方题解

• 官方题解还是动态规划的方法，但是它列在了一维动态规划的题型里迷惑性太强了，一直在想一维数组怎么可能表达2*n的格子呢，不过确实不是我想得到的。

思路

1. 总的来说就是按列分状态讨论情况，该列会有4中情况：上下都空，只有上面有，只有下面有，上下都有。因为到达每列前，之前的列都处理完了，所以每种状态可由不同的状态转移过来：
   1. 上下都空：前面只有可能全满，也就是状态4转移过来。
   2. 只有上面有：前一列可能是上下都空，然后插入一个上面凸起的tromino；也可能是只有下面有，然后再上面插入一个domino。
   3. 只有下面有：跟只有上面有对称。
   4. 上下都有：前一列可能全空，铺了两个domino；也可能只有上面或下面，补了一个tromino；也可能全满，这时候就在本列补一个domino即可。
2. 
3. 官解定义了状态转移方程如上，补充第一列的初始状态dp[0][0]=0，dp[0][1]=0，dp[0][2]=0，dp[0][3]=1，前三种方案不存在所以是0，往后迭代就有了（dp[i]考虑的都是第i-1列的情况，让dp[0][3]等于1其实就是考虑初始状态什么都没放的时候的一种初始状态，可以理解成一个额外的前置列全满，为了传递给后一项，所以需要放在状态3）。
4. 因为加法会溢出，所以尽量每次加法都取一下模。

代码实现

class Solution {
public:
    int numTilings(int n) {
        int dp[n+1][4];
        long long mod = 1e9 + 7;
        dp[0][0] = 0;
        dp[0][1] = 0;
        dp[0][2] = 0;
        dp[0][3] = 1;
        for(int i = 1; i <= n; i++) {
            dp[i][0] = dp[i-1][3] % mod;
            dp[i][1] = (dp[i-1][0] + dp[i-1][2]) % mod;
            dp[i][2] = (dp[i-1][0] + dp[i-1][1]) % mod;
            dp[i][3] = (dp[i-1][0] + dp[i-1][1] + dp[i-1][2] + dp[i-1][3]) % mod;
        }
        return dp[n][3];
    }
};

复杂度分析

• 时间复杂度：O(n)。
• 空间复杂度：O(1)。