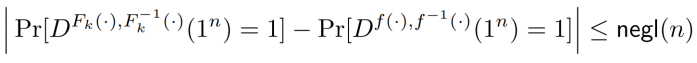一个核心概念：人工粘性

考虑经典的双曲守恒律方程
$$\frac{\partial u}{\partial t}+\frac{\partial f}{\partial x}=0$$
可以写成守恒形式的数值格式
$$u_i^{n+1}=u_i^n-\lambda \left({\hat{f}}_{i+1/2}^n-{\hat{f}}_{i+1/2}^n\right)$$
式中$\lambda$是时间步长与空间步长之比。$\hat{f}$则是面上的数值通量。各种格式的最终目的就是设法给出数值通量的近似。
为了减小间断处的震荡，一种有效的方法是在方程右端添加人工粘性项
$$\frac{\partial u}{\partial t}+\frac{\partial f}{\partial x}=\frac{\Delta x^2}{\Delta t}\frac{\partial }{\partial x}\left(Q\frac{\partial u}{\partial x}\right)$$相似地，也可差分得到下式
$$u_i^{n+1}=u_i^n-\lambda \left({\hat{f}}_{i+1/2}^n-{\hat{f}}_{i+1/2}^n\right)+1/2\left(Q_{i+1/2}{\Delta }^{+}{u}_i^n-Q_{i-1/2}{\Delta }^{-}{u}_i^n\right)$$
可以将右侧第三项与数值通量合并，得到新的数值通量
$${\bar{f}}_{i+1/2}^n={\hat{f}}_{i+1/2}^n-\frac{Q_{i+1/2}}{2\lambda }{\Delta }^{+}{u}_i^n$$$${\bar{f}}_{i-1/2}^n={\hat{f}}_{i-1/2}^n-\frac{Q_{i-1/2}}{2\lambda }{\Delta }^{-}{u}_i^n$$

这里可以看出“人工粘性”可增加逆梯度方向上的通量，即如果$u_{i+1}^n>u_i^n$，那么“人工粘性”将会减少$i+1/2$面上的正向通量。相反地，负人工粘性则会增加$i+1/2$面上的通量。合适地选取、改变、调整负人工粘性则是开发高分辨率格式的核心问题。

经典格式

中心差分格式

$${\hat{f}}_{i+1/2}^n=\frac{f_i+f_{i+1}}{2}$$

一阶迎风格式

$${\hat{f}}_{i+1/2}^n=\frac{f_i+f_{i+1}}{2}-\frac{1}{2}\left|a_{i+1/2}^n\right|\left(u_{i+1}-u_i\right)$$
式中右端第二项为一阶迎风格式引入的数值粘性

Lax-Fridrichs一阶格式

$${\hat{f}}_{i+1/2}^n=\frac{f_i+f_{i+1}}{2}-\frac{1}{2\lambda }\left(u_{i+1}-u_i\right)$$
第二项是数值粘性，该格式的数值粘性非常大

Lax-Wendroff二阶格式

$${\hat{f}}_{i+1/2}^n=\frac{f_i+f_{i+1}}{2}-\frac{1}{2}\lambda {\left(a_{i+1/2}^n\right)}^2\left(u_{i+1}-u_i\right)$$

注意："数值粘性"来源于格式本身，"人工粘性"来源于人为添加的扩散项，虽然表象不同，但二者的本质是相同的。

高分辨率TVD格式的原理

尝试在1阶TVD格式的基础上添加负的"人工粘性“。这个“人工粘性”必须是非线性的，使得：在光滑区域达到二阶格式，而在间断区域回归到一阶格式。

A 通量修正法

Harten¹提出的通量修正法即是在1阶TVD格式的基础上修正物理通量$f$以部分抵消原格式的截断误差。这个修正量（事实上的“人工粘性”）必须是非线性的，使得：在光滑区域完全抵消低阶格式的数值粘性，并趋近于二阶L-W格式的数值粘性，达到二阶格式。而在间断区域回归到一阶格式。为了实现这一目标，必须平衡好${\bar{f}}_{i+1/2}^n$中蕴含的“数值粘性”部分与“人工粘性”部分。

B 通量限制器

与Harten的想法类似，但是不再修正"物理通量$f$"，而是直接修正"数值通量${\bar{f}}_{i+1/2}^n$"。将高阶格式的数值通量写为低阶格式的数值通量与反扩散通量之和，为了使格式总变差不增（TVD条件），需要限制反扩散通量的大小。这就是通量限制器。反扩散通量实质上就是负的"人工粘性"。
比如，取使用L-W格式作为高阶格式
$${\left[{\hat{f}}_{i+1/2}^n\right]}_{\mathrm{H}\mathrm{i}\mathrm{g}\mathrm{h}}=\frac{f_i+f_{i+1}}{2}-\frac{1}{2}\lambda {\left(a_{i+1/2}^n\right)}^2\left(u_{i+1}-u_i\right)$$
再使用一阶迎风格式作为低价格式
$${\left[{\hat{f}}_{i+1/2}^n\right]}_{\mathrm{L}\mathrm{o}\mathrm{w}}=\frac{f_i+f_{i+1}}{2}-\frac{1}{2}\left|a_{i+1/2}^n\right|\left(u_{i+1}-u_i\right)$$
两种格式进行组合
$${\hat{f}}_{i+1/2}^n={\left[{\hat{f}}_{i+1/2}^n\right]}_{\mathrm{L}\mathrm{o}\mathrm{w}}+\phi \left({\left[{\hat{f}}_{i+1/2}^n\right]}_{\mathrm{H}\mathrm{i}\mathrm{g}\mathrm{h}}-{\left[{\hat{f}}_{i+1/2}^n\right]}_{\mathrm{L}\mathrm{o}\mathrm{w}}\right)$$$$=\frac{f_i+f_{i+1}}{2}-\frac{1}{2}\left|a_{i+1/2}^n\right|\left(u_{i+1}-u_i\right)+\phi \left(-\frac{1}{2}\lambda {\left(a_{i+1/2}^n\right)}^2\left(u_{i+1}-u_i\right)+\frac{1}{2}\left|a_{i+1/2}^n\right|\left(u_{i+1}-u_i\right)\right)$$$$=\frac{f_i+f_{i+1}}{2}-\frac{1}{2}\left|a_{i+1/2}^n\right|\left(u_{i+1}-u_i\right)+\phi \frac{\mathrm{sgn}\left({\nu }_{i+1/2}^n\right)-{\nu }_{i+1/2}^n}{2}{a}_{i+1/2}^n\left(u_{i+1}-u_i\right)$$
式中的$\phi$表示通量限制器，对于光滑区域取1，达到二阶L-W格式，对于间断区域取0，恢复到一阶迎风格式。首先使用变量$r$描述解的光滑程度
$$r_{i+1/2}=\{\begin{array}{l}\frac{u_i-u_{i-1}}{u_{i+1}-u_i},a_{i+1/2}>0\\ \frac{u_{i+2}-u_{i+1}}{u_{i+1}-u_i},a_{i+1/2}<0\end{array}$$
然后使用$r$描述通量限制器$\phi$，通量限制器的表达式有许多，详见Sweby²的工作

C 斜率限制器

采用分片线性函数重构解，在单元面上应用TVD模板。
$${\hat{f}}_{i+1/2}\left(u_i,u_{i+1}\right)\to {\hat{f}}_{i+1/2}\left(u_{i+1/2}^L,u_{i+1/2}^R\right)$$$$u_{i+1/2}^L=u_i+s_i\frac{\Delta x}{2},u_{i+1/2}^R=u_{i+1}-s_{i+1}\frac{\Delta x}{2}$$可以证明，在一定条件下，前者是一阶TVD的，那么后者是二阶TVD的
需要使用限制器来限制线性函数的斜率以实现TVD格式。其本质与通量限制器相同。限制后的斜率与通量限制器之间的关系是
$$s_i=\left(\frac{u_{i+1}-u_i}{\Delta x}\right)\phi \left(r_{i+1/2}\right)$$具体可参考MUSCL格式

---

1. HARTEN A. High resolution schemes for hyperbolic conservation laws[J]. Journal of Computationalphysics, 1983(49): 357-393. ↩︎

2. SWEBY P K. High resolution schemes using flux limiters for hyperbolic conservation laws[J]. Siam Journal On Numerical Analysis, 1984, 21(5): 995-1011. ↩︎