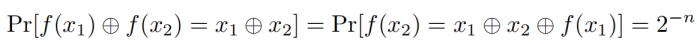目录

伪随机置换

PROPOSITION 3.26 伪随机置换和伪随机函数的关系

DEFINITION 3.27 强伪随机置换

---

伪随机置换

我们称F是含参数k的置换，当且仅当

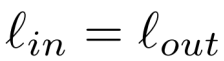
且对于所有k，

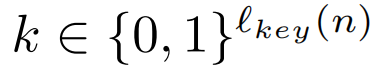
Fk是一对一的，即是满射的。

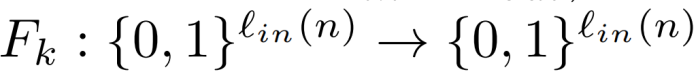
其中 lin 称为F的块长度

对于给定的 k、x和k、y，如果

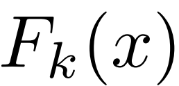
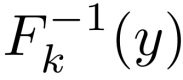
上面两个式子都可以在多项式时间内计算，则称这个伪随机置换是高效率的。

除非另有说明，我们假设F保留长度的，因此

---

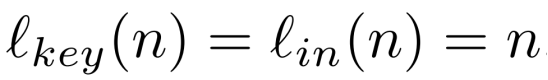
PROPOSITION 3.26 伪随机置换和伪随机函数的关系

设 F 是一个随机置换，如果 lin(n) ≥ n，则 F 也是一个伪随机函数

---

DEFINITION 3.27 强伪随机置换

设F：{0,1}∗×{0,1}∗→{0,1}∗是一个有效的、长度保留的、含参数k的置换。如果对于所有的PPT区分器D，存在一个可忽略函数negl，使得：

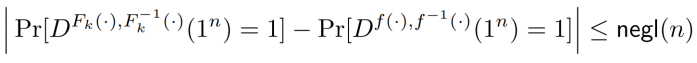
 其中f∈Perm_n。我们称F为一个强伪随机置换