( 一).图的基本结构

图是有顶点的有穷非空集合和顶点之间的组成集合，通常表示为: G=(V,E).其中,G表示一个图,E是顶点之间边的集合。

(1).无序偶对.

若顶端v1和顶端v2之间的边没有方向**,则称这条边为无向边,用无序偶对(v1,v2)表示。

(2).有序偶对

若顶端v1和顶端v2之间的边有方向,则称这条边为有向边(也称为弧),用有序偶对<v1,v2>表示,v1成为弧尾,v2成为弧头

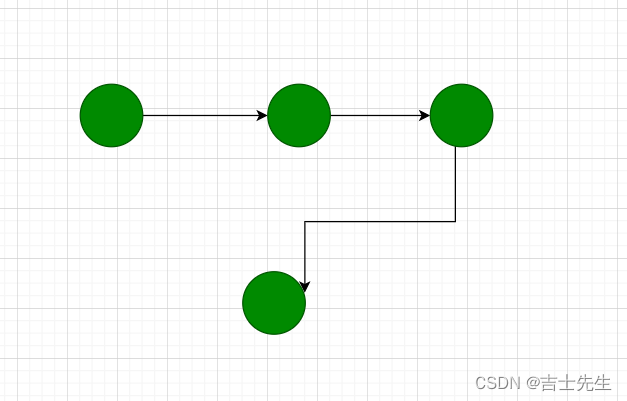
(3).有向图和无向图

如果图的任意两个顶点之间的边都是无向边，则称这个图为无向图 否则称为有向图。

(4).权

(weight)通常是对边赋予的有意义的数值量,在实际应用中,权可以有具体的含义。

(5).网图

:边上带权的图称为带权图或网图。eg:有向网图,无向网图。

(二).图的基本术语

(1).邻接.依附

在无向图中,对于任意两个顶点v1和v2,若存在边(v1,v2),则称为顶点v1和v2互为领接点,同时称为哦边(v1,v2)依附于顶点v1和v2.

(2).有向完全图,无向完全图

有无向图中,如果任意两个顶点之间都存在边,'则称为该图为无向完全图,含有n个顶点的无向完全图有n*(n-1)/2条边。

在有向图中,如果两个顶点之间都存在互为反方向的弧,则称该图为有向完全图。含有n个顶点的有向完全图有n*(n-1)条边

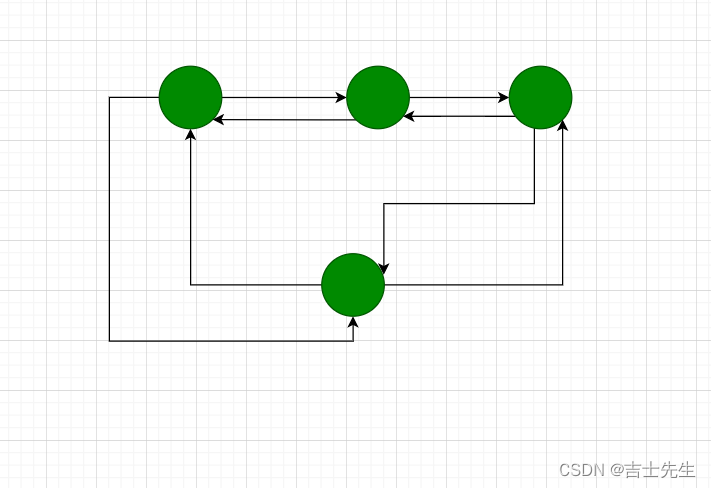
(3).顶点的度,入度,出度

在无向图中,顶点v的度是指依附于该顶点的边的个数，记为TD(v),在具有n个顶点e条边的无向图中，成立 各个顶点的度之后＝2*e

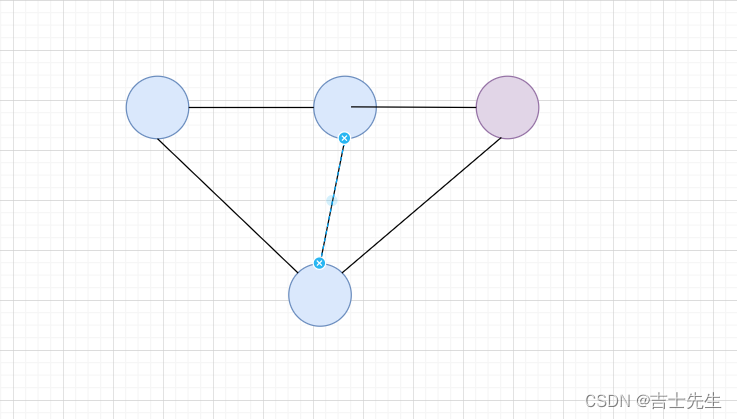
在有向图中,顶点v的入度是指以该顶点为弧头的弧的个数,记为ID(v);顶点v的出度是指以该顶点为弧尾的弧的个数，记为OD(v)在具有n个顶点e条边的有向图中成立 各个顶点的入度之和＝各个顶点出度之和＝e

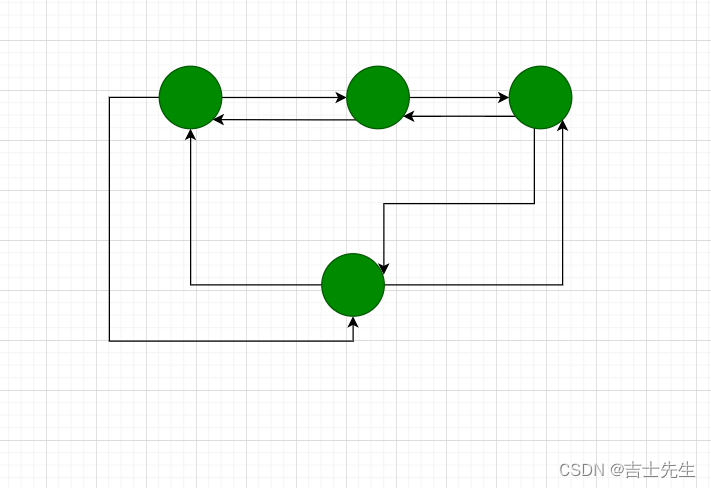
(4).路径 路径长度 回路

路径上边的数目称为路径长度,第一个顶和最后一个顶点的相同路径称为回路。两个顶点之间的边就是路径。

(5).简单路径 简单回路

顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外,其余顶点不重复 出现的回路称为简单回路。

(6).子图

图A中包含图B，则称为图B包含图A.

(7).连通图 连通分量

在无向图中，若顶点v1和顶点v2之间存在路径，则称为v1和v2之间是连通的,若任意顶点之间均存在路径,则称该图是连通图。

非连通图的极大连通子图称为连通分量。

非连通图

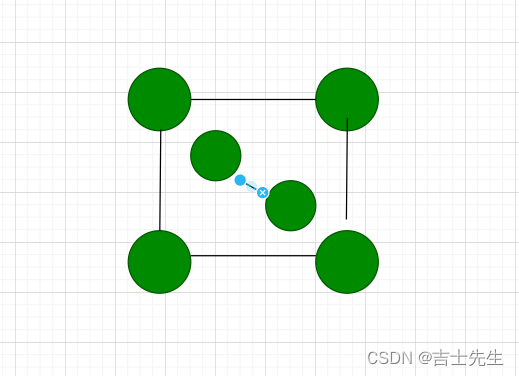
连通分量

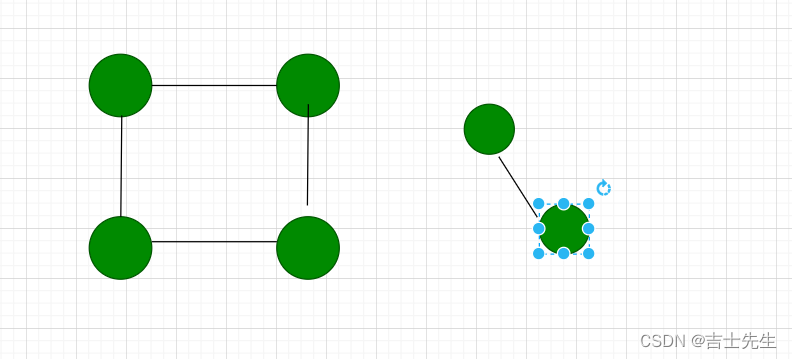
(8).强连通图 强连通分量

在有向图中,对任意两个顶点,都存在路径,则称该有向图是强连通图。

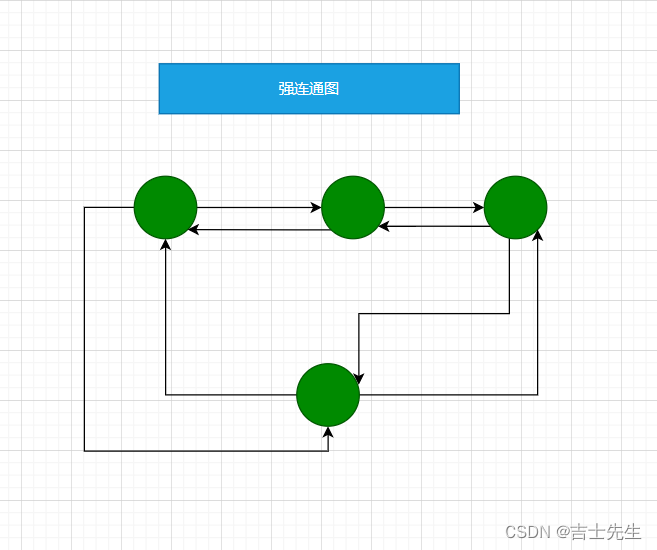
非强连通图的极大强连通图子图成为强连通分量。

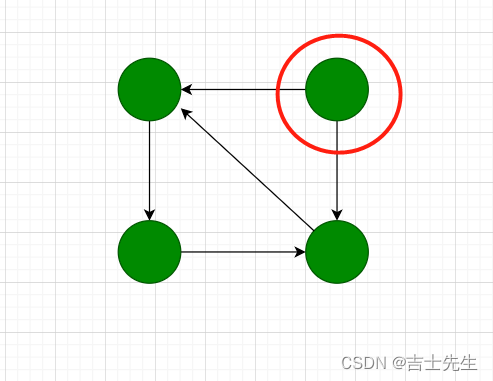
强连通分量

(三).图的遍历

(1).深度优先遍历(相似于栈)

深度优先遍历的主要思想: 新进后出:
(1).访问顶点v。
(2).从v的未被访问的邻接点选取一个顶点w，然后从w深度优先遍历。
(3).如果访问途中没有遇到未被访问的顶点，那么就先进的后出(栈)
(4).重复上诉步骤，直至所有顶点被访问完毕。

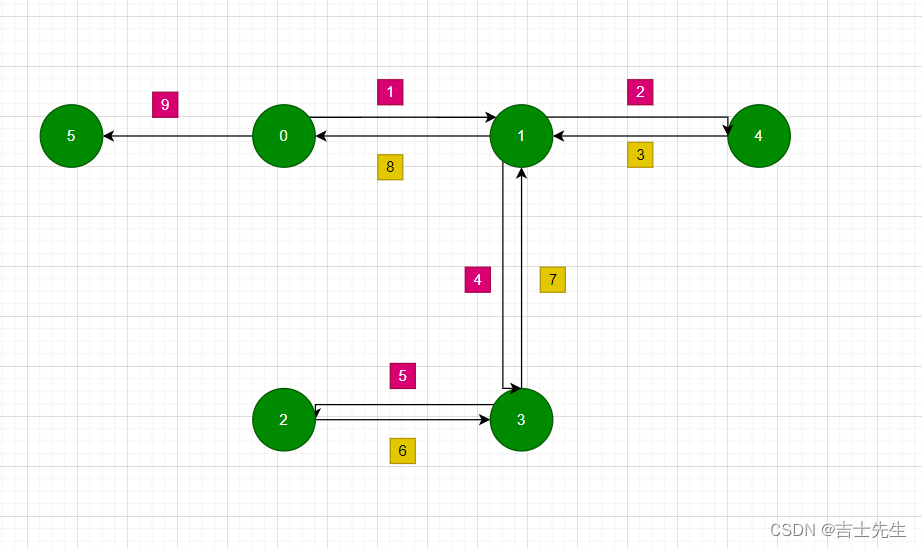
(2).广度优先遍历(相似于层序遍历)

以顶点v为起始点，有近到远，一次访问和v有路径相通且路径长度为1，2..的
顶点，为了使先被访问顶点的邻接点"先于"后被访问顶点的邻接点"被访问"

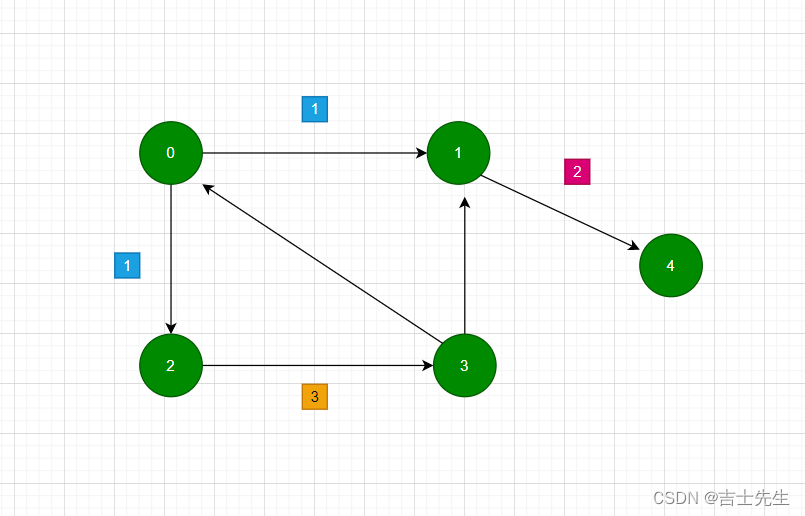
(四).图的存储结构及实现

(1).邻接矩阵的存储结构

图的邻接矩阵存储也称数组表示法，用一个一维数组存储图中的顶点，用一个二维
数组存储图中的边(即个顶点之间的邻接关系)，存储顶点之间的邻接关系的二维数组
称为邻接矩阵，设图G=(V,E)有n个顶点，则邻接矩阵是一个n*n的方阵

无向图

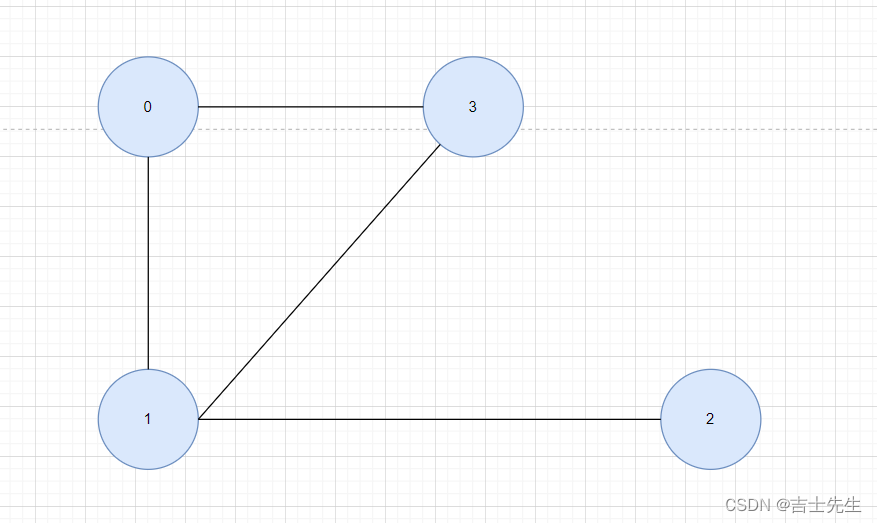
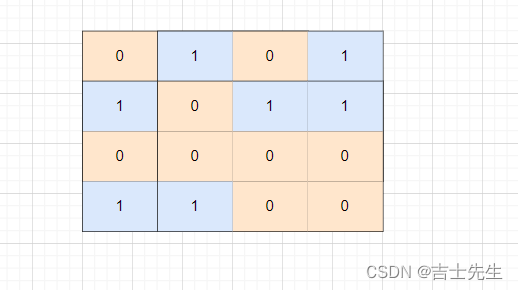
1.无向图的邻接矩阵一定是对称矩阵，而有向图的矩阵不一定对称。
2.在无向图，顶点i的度等于邻接矩阵中第i行(或第i列)非零元素的个数。
3.对于有向图，顶点i的出度等于邻接矩阵中第i行非零元素的个数；顶点
i的入度等于邻接矩阵中第i列非零元素的个数
4.判断顶点 i 和 j 之间是否存在边，只需要测试邻接矩阵中相应位置的元素
edge[i][j]，若其值为1，则有边;否则,顶点 i 和 j
之间不存在边
5.查找顶点i的所有邻接点,扫描邻接矩阵的第i行，若edge[i][j]的值为1，则顶点j是顶点i 的邻接点

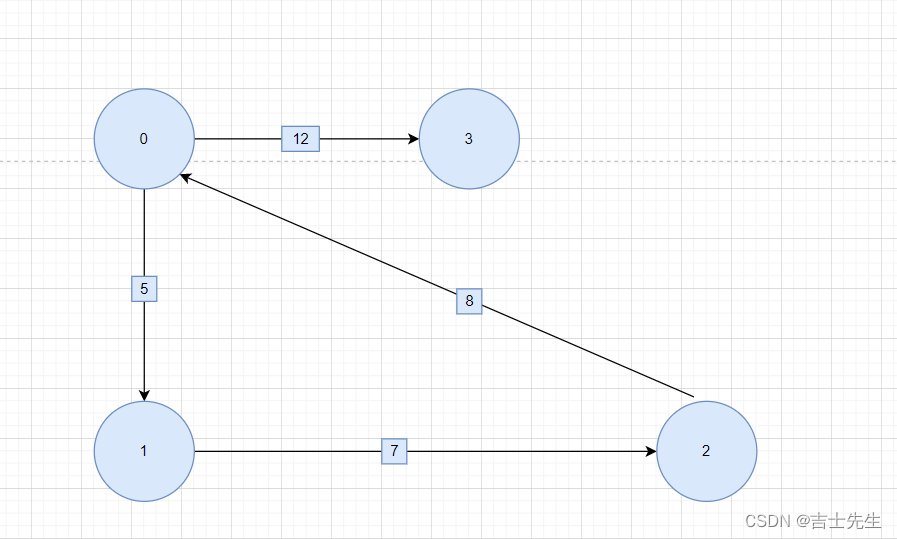
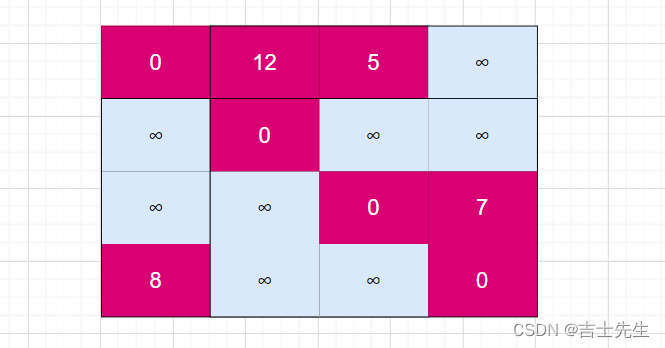
(2).邻接表的存储结构

邻接表是一种顺序存储与链式存储相结合的存储方法，像极了孩子表示法
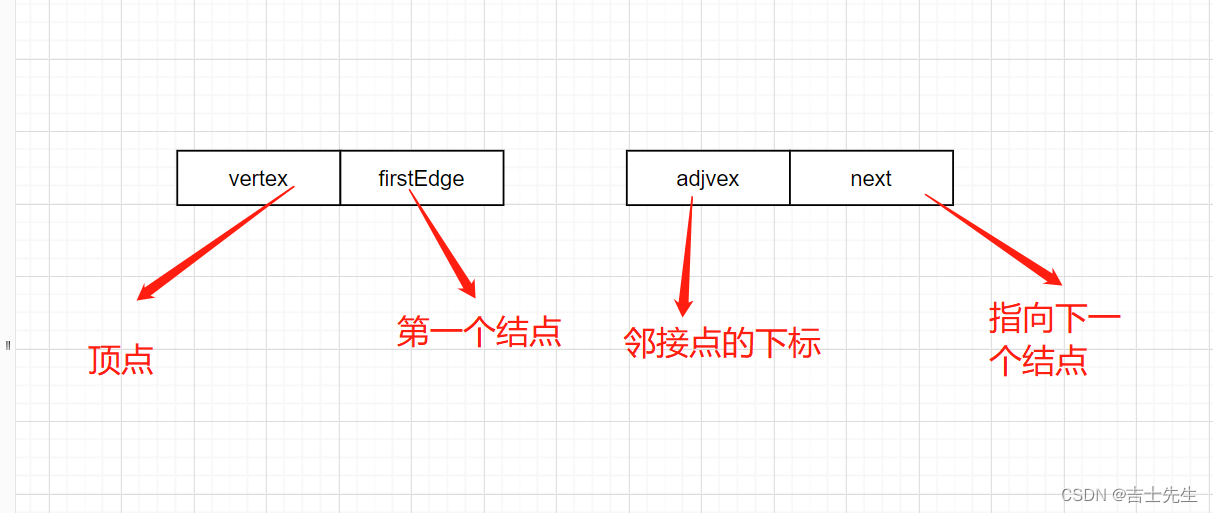
顶点表：存储边表头指针的数组和存储顶点的数组构成了邻接表的表头数组。
1.vertex为数据域，存储顶点信息。
2.firstEdge为指针域，指向边的第一个结点。
3.adjvex为邻接点域，存放该顶点的邻接点在顶点表中的下标
4.next为指针域，指向边表的下一个结点

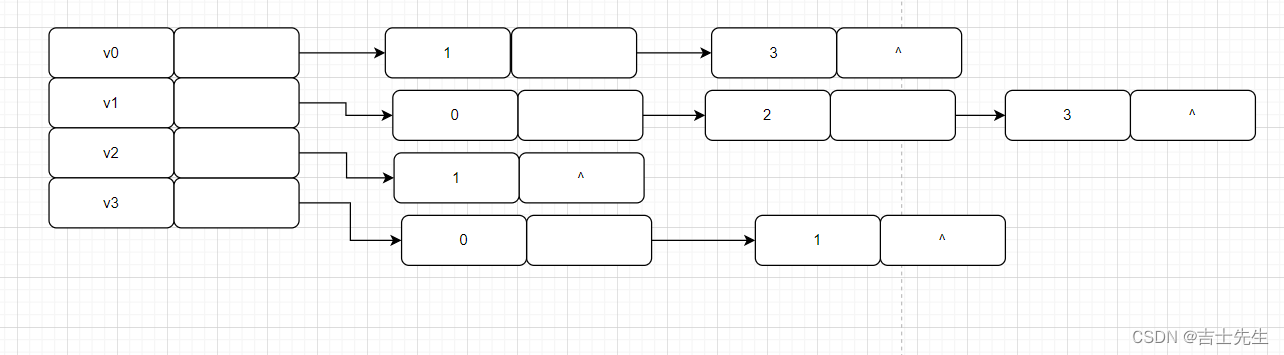
无向图


有向图

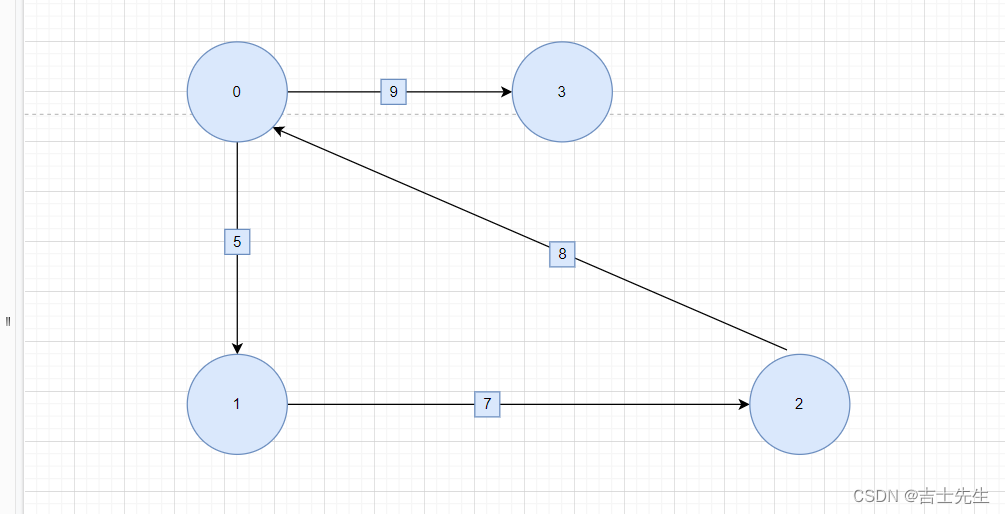
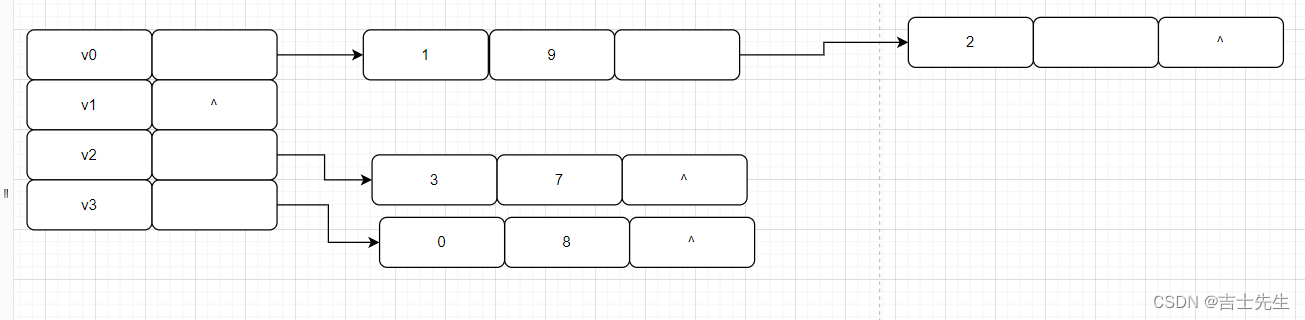
1.对于无向图，顶点i的度等于顶点i的边表中的节点个数。
2.对于有向图，顶点 i 的出度等于顶点 i 的出边表中的结点个数。
3.顶点 i 的入读等于所有出边表中以顶点 i 为邻接点的结点个数
4.判断从顶点到顶点j是否存在边，只需要测试顶点 i 的边表中是否存在临接点域为 j 的结点
5.查找顶点 i 的所有邻接点，只需要遍历顶点i的边表，该边表中的所有结点都是顶点的邻接点。

(3).邻接矩阵和邻接表的比较

(五).最小生成树

(1).生成树:

连通图的生成树是否包含图中全部顶点的一个极小连通图。在生成树中添加一条属于原图中的边必定会产生回路。

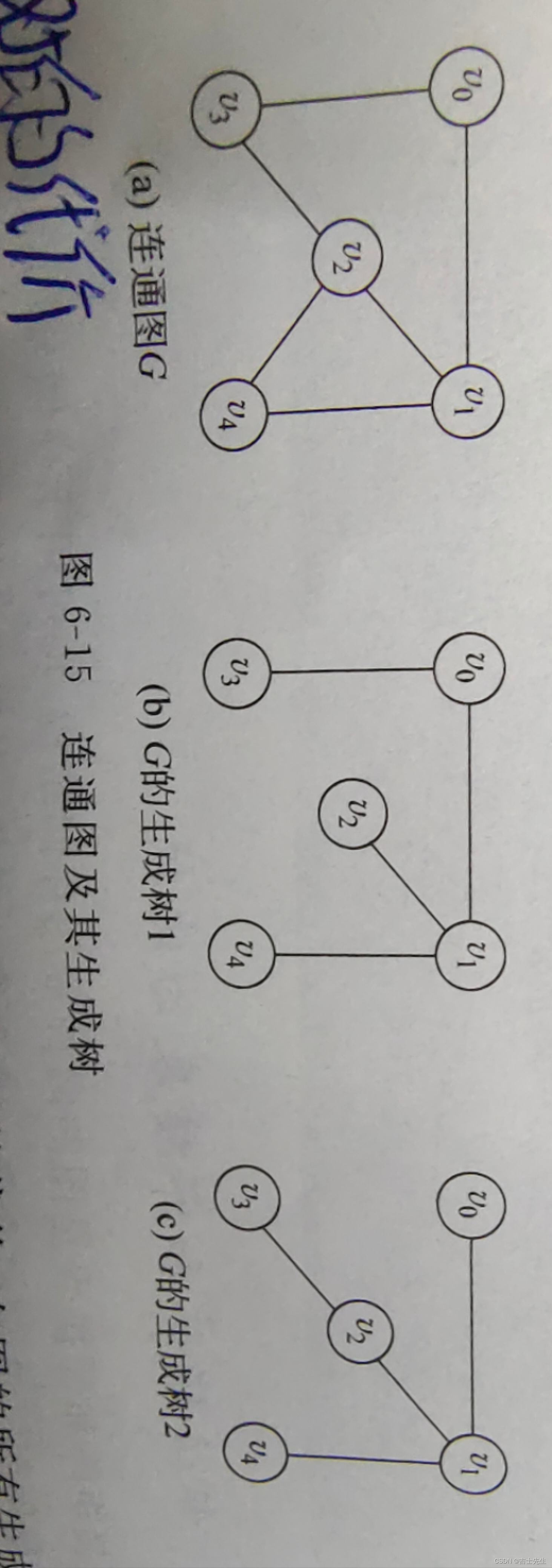
(2).生成树的代价

无向连通网的生成树上个边的权值之和称为该生成树的代价，在途中的所有生成树中，代价最小的生成树称为最小生成树。

(3).prim算法(两个集合)

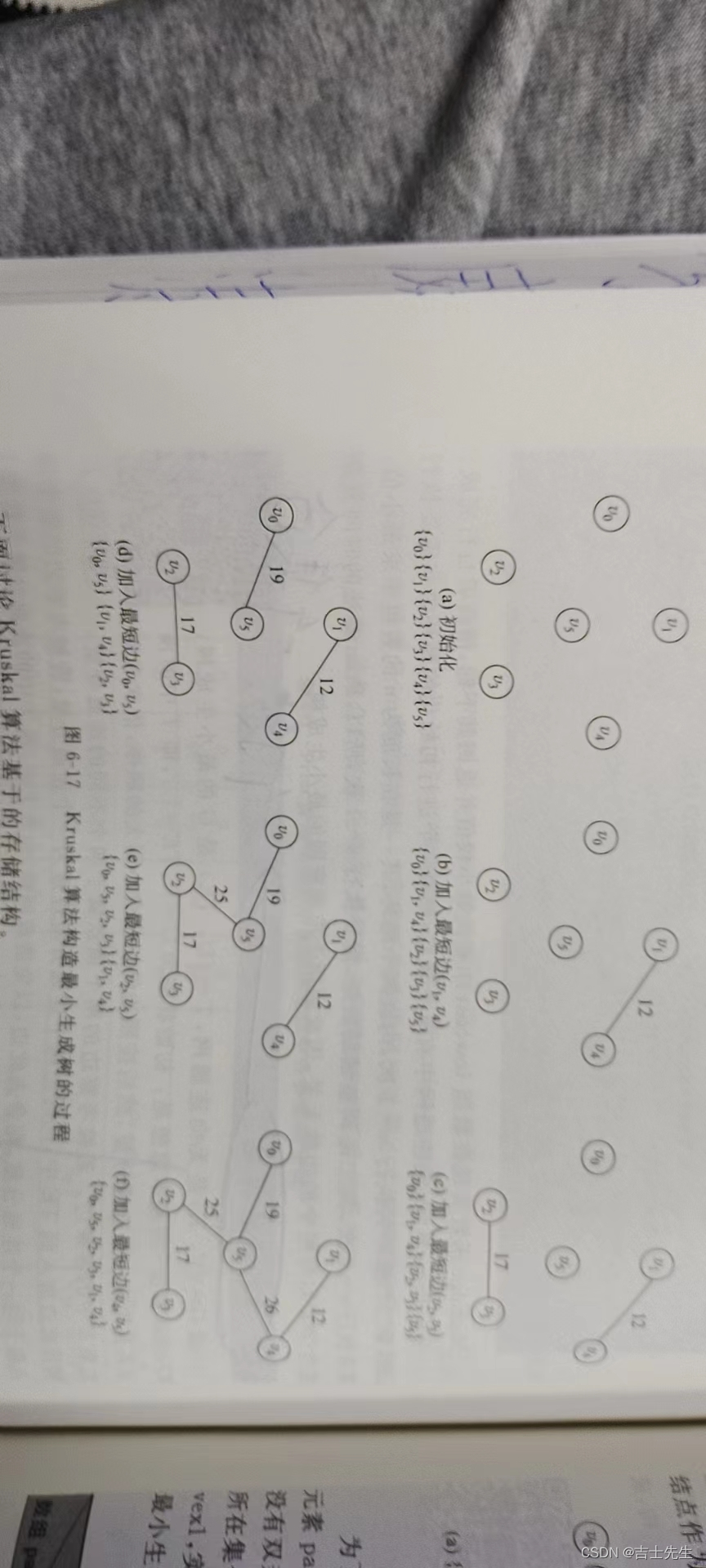
(2).kruskal算法(一个顶点，一个集合)