题目分析

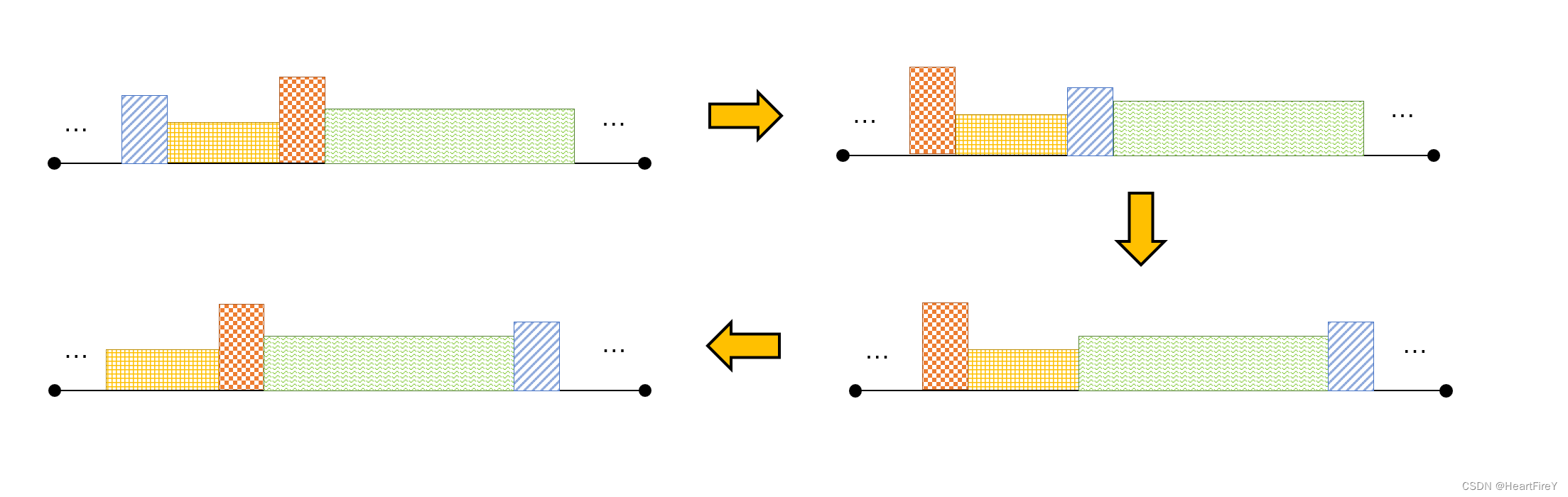
首先需要观察到一个性质：在最优方案下的操作一定是首先交换距离最近能交换的两个点来达到交换的效果，这个很好理解：题目要求如果要交换两个人的位置，中间的人的身高必须严格小于这两个人，因此合法的交换操作仅可能发生在距离最近的可交换点对之间。每次交换花费仅可能耗费一次操作。

那么我们可以发现，如果从身高最小的往上交换，每次的操作次数等同于：
$$abs((在g数组中交换到首位的操作步数)-(在h数组中交换到首位的操作次数))$$
为什么要从身高最小的向上交换？因为当身高小的到达正确位置后，不会再对后续身高更高的交换操作产生影响。

那么我们发现交换的首位的操作次数实际上就是求个逆序对即可。然后按顺序统计答案即可。

那么如何求操作序列呢？我们仍按照上述的策略来确定操作，但是我们很快会发现：每次操作我们都需要很快快的求得以下几个量：假设当前位置为$p$：

• 求得首个$l\_max\le p$且$g[l\_max]\ge g[p]$；
• 求得首个$r\_max\ge p$且$g[r\_max]\ge g[p]$。

然后我们会很熟悉的发现，只需要上个线段树+二分就可以解决这个问题。但是这样做还是有个问题：

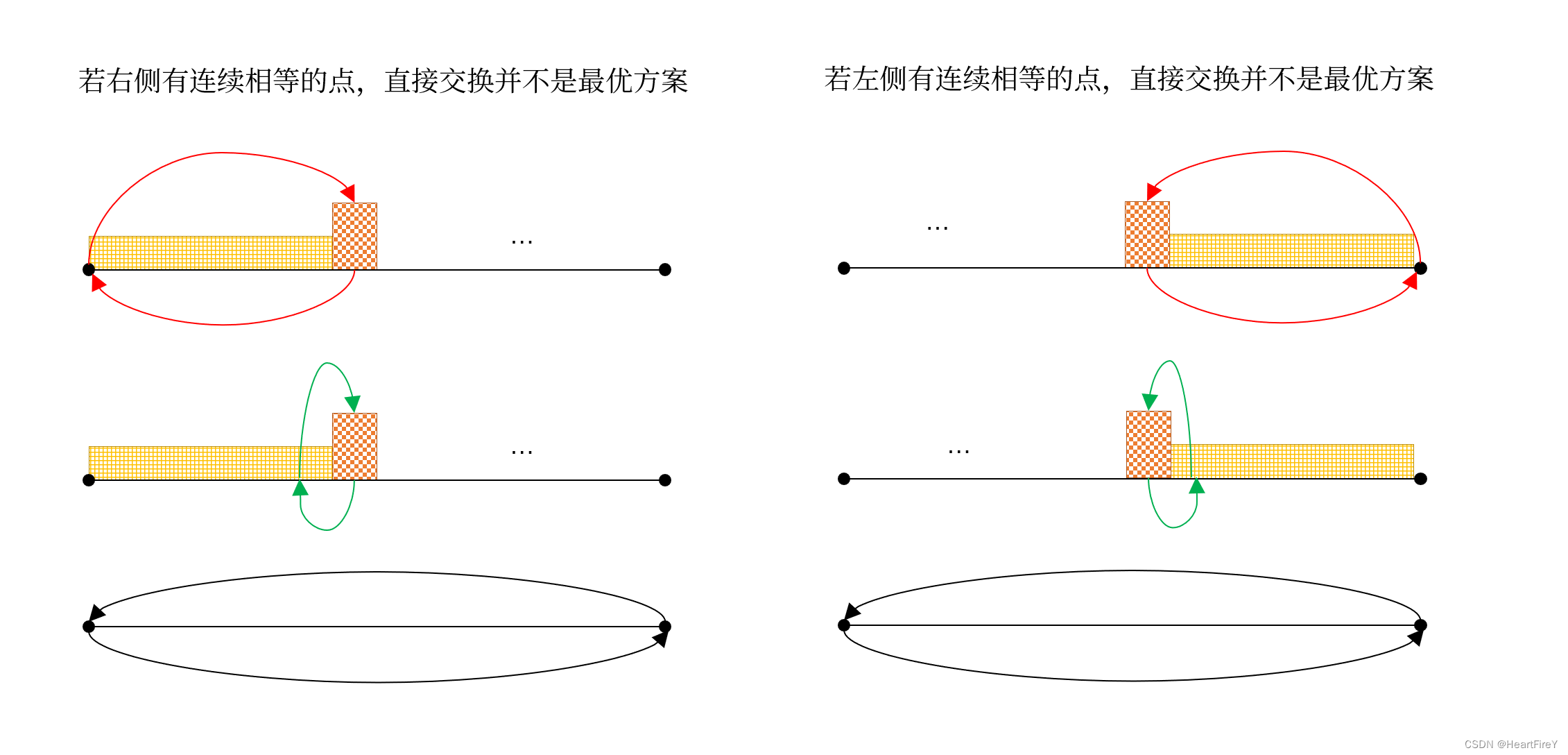
如果存在连续相等的序列，那么就求错了，因为跨过了一大段无意义的交换。这该怎么办呢？

假设原始位置为$a$，待抵达位置为$b$，分类讨论：

• 如果$a<b$：
  • 每次交换时，先找到$a$右侧最近的$r\_max$，然后对$r\_max$找到左侧最近的$l\_max$(注意这里的$l\_max$是相对$h[r\_max]$而言的，$r\_max$是相对$h[a]$而言的)，然后使用该$l\_max$和$r\_max$进行交换即可。
• 如果$a>b$:
  • 每次交换时，先找到$a$左侧最近的$l\_max$，然后对$l\_max$找到右侧最近的$r\_max$，然后使用该$l\_max$和$r\_max$进行交换即可。

上面两个过程实际上是一对镜像操作。如此一来，就避免的无意义的连续相等段内的交换(这些段的错误贡献实际上在逆序对统计时也没有统计到答案里(前提是要稳定排序否则会错)，但是却会影响操作的构造)。

剩下的模拟上述过程即可。注意排序必须要稳定排序！否则会使逆序对计数产生错误(连续相同段)。

再注意，输出上限$2e5$，不要企图像HeartFireSB一样输出所有答案。

Code

#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
// 15016413052
const int N = 4e5 + 10, INF = 1e9 + 7;
int g[N], h[N];

struct Fenwick{
    int tree[N], len;
    #define lowbit(x) ((x) & (-x))
    inline void update(int i, int x){
        for(int pos = i; pos <= len; pos += lowbit(pos)) tree[pos] += x;
    }

    inline int getsum(int i, int ans = 0){
        for(int pos = i; pos > 0; pos -= lowbit(pos)) ans += tree[pos];
        return ans;
    }
    inline int query(int l, int r) {
        return getsum(r) - getsum(l - 1);
    }
} fh, fg;

int idg[N], idh[N], gid[N], n;

namespace SegTree{
    #define ls rt << 1
    #define rs rt << 1 | 1
    #define lson ls, l, mid
    #define rson rs, mid + 1, r

    int tree[N << 2];
    
    inline void push_up(int rt) { tree[rt] = max(tree[ls], tree[rs]); }

    void update(int rt, int l, int r, int pos, int val) {
        if(l == r) return tree[rt] = val, void();
        int mid = l + r >> 1;
        if(mid >= pos) update(lson, pos, val);
        else update(rson, pos, val);
        push_up(rt);
    }
    // L = 1, R = pos
    int queryl(int rt, int l, int r, int pos, int val) {
        if(l == r) { 
            if(tree[rt] >= val) return l;
            else return -1;
        }
        if(l >= 1 && r <= pos && tree[rt] < val) return -1;
        int mid = l + r >> 1;
        if(mid >= pos) return queryl(lson, pos, val);
        int res = queryl(rson, pos, val);
        if(res != -1) return res;
        return queryl(lson, pos, val);
    }
    // L = pos, R = n
    int queryr(int rt, int l, int r, int pos, int val) {
        if(l == r) {
            if(tree[rt] >= val) return l;
            return INF;
        }
        if(l >= pos && r <= n && tree[rt] < val) return INF;
        int mid = l + r >> 1;
        if(mid < pos) return queryr(rson, pos, val);
        int res = queryr(lson, pos, val);
        if(res != INF) return res;
        return queryr(rson, pos, val);
    }
}

inline void solve() {
    cin >> n; 
    fh.len = fg.len = n + 10;
    for(int i = 1; i <= n; i++) cin >> g[i];
    for(int i = 1; i <= n; i++) cin >> h[i];
    iota(idg, idg + 10 + n, 0);
    iota(idh, idh + 10 + n, 0);
    stable_sort(idg + 1, idg + 1 + n, [&](int a, int b){ return g[a] < g[b]; });
    stable_sort(idh + 1, idh + 1 + n, [&](int a, int b){ return h[a] < h[b]; });
    int cnt = 0;
    for(int i = 1; i <= n; i++) {
        int a = idg[i], b = idh[i];
        fg.update(a, 1);
        fh.update(b, 1);
        cnt += abs((a - fg.getsum(a)) - (b - fh.getsum(b)));
        // cout << "cnm -> " << a << ", " << b << " :: " << abs((a - fg.getsum(a)) - (b - fh.getsum(b))) << endl;
    }
    cout << cnt << endl;
    if(cnt == 0) return;   
    for(int i = 1; i <= n; i++) SegTree::update(1, 1, n, i, g[i]);
    for(int i = 1; i <= n; i++) gid[idg[i]] = i;
    // for(int i = 1; i <= n; i++) cout << gid[i] << " \n"[i == n];
    int moves_cnt = 0;
    auto op = [&](int a, int b) {
        // if(moves_cnt >= cnt) return;
        swap(g[a], g[b]);
        swap(gid[a], gid[b]);
        swap(idg[gid[a]], idg[gid[b]]);
        SegTree::update(1, 1, n, a, g[a]);
        SegTree::update(1, 1, n, b, g[b]);
        cout << a << " " << b << endl;
        if(++moves_cnt == 200000) exit(0);
    };
    for(int k = 1; k <= n; k++) {
        int a = idg[k], b = idh[k];
        // cout << "NEW ROUND #" << k << endl;
        while(a < b) {
            int rmax = SegTree::queryr(1, 1, n, a, g[a] + 1);
            if(rmax > n) break;
            int lmax = SegTree::queryl(1, 1, n, rmax - 1, g[a]);
            // cout << "#Query1 -> a = " << a << ", b = " << b << "; rmax = " << rmax << ", lmax = " << lmax << endl;
            op(lmax, rmax);
            if(lmax == a) a = rmax;
        }

        while(a > b) {
            int lmax = SegTree::queryl(1, 1, n, a, g[a] + 1);
            if(lmax < 1) break;
            int rmax = SegTree::queryr(1, 1, n, lmax + 1, g[a]);
            // cout << "#Query2 -> a = " << a << ", b = " << b << "; lmax = " << lmax << ", rmax = " << rmax << endl;
            op(lmax, rmax);
            if(rmax == a) a = lmax;
        }
        // cout << "idg: ";
        // for(int i = 1; i <= n; i++) cout << idg[i] << " \n"[i == n];
    }
    for(int i = 1; i <= n; i++) assert(g[i] == h[i]);
}

signed main() {
    //    freopen("stdin.in", "r", stdin);
    //    freopen("stdout2.out", "w", stdout);
    ios_base::sync_with_stdio(false), cin.tie(0);
    solve();
    return 0;
}