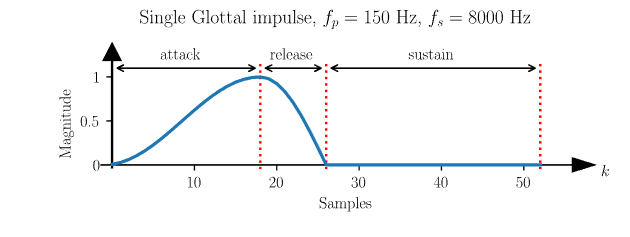
对于 0<t<tpeak，gattack(t)
攻击部分，即上升分支的时间，时间 t 的范围从 0 秒到最大峰值时间 tpeak ，图示例中选择为大约总长度的 35%，即 tpeak=35%⋅T0，或者在样本 Lattack=⌊35%⋅Lg⌉ 中，运算符 ⌊⋅⌉ 是舍入运算符，在 Python 用 np.round()
对于 tpeak<t<tc，grelease(t)
对于 tc<t<T0 ，gsustain(t)
数学上定义为：
脉冲长度（以秒为单位）T0 = 1/Fp
样本长度 Lg=Fs/Fp的绝对值

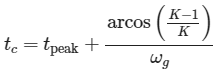
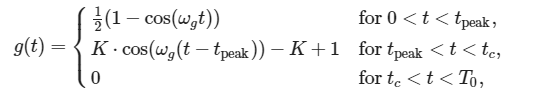
gattack

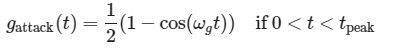
# reminder (lab-sheet 1), generation of a sine signal
fs = 8000                          # samples per second
dt = 1/fs                          # seconds per sample

fp = 150                           # pitch frequency (of complete glottis pulse)
Lg = np.floor(fs/fp)               # number of samples per glottis pulse
Lattack = np.round(0.35*Lg)        # length of the attach part
tPeak = Lattack / fs               # time in seconds of the attack part

print('A period of a signal with frequency of '+str(fp)+' Hz is '+str(1/fp)+' seconds or '+str(fs/fp)+' samples')
print('The glottis impulse has thus a length of '+str(Lg))

omega_g = np.pi / tPeak            # (angular) frequency

# let's first create a full period of the sinus (since we know how this works)
t1 = np.arange(0,Lg/fs,dt)         # time vector in seconds (one period length)
x1 = np.cos(omega_g*t1)            # one period of cosine wave signal

# now a raised cosine
x2 = 0.5*(1-np.cos(omega_g*t1))    # rased cosine signal (same time vector as before)

# sine signal of frequency fp Hz
tAttack = np.arange(0,tPeak,dt)         # shorter time vector in seconds
gAttack = 0.5*(1-np.cos(omega_g*tAttack))     # same raised cosine signal as before for shorter time

plt.figure(figsize=(8,6))
plt.subplot(3,1,1)
plt.plot(x1,marker='.',label='$x_1(t)=\cos(\omega_g t)$')
plt.xlim(-1,Lg)
plt.ylim(-1.1,1.1)
plt.xlabel('dicrete time in samples $k$')
plt.legend(loc='upper right')

plt.subplot(3,1,2)
plt.plot(x2,marker='.',label='raised cosine $x_2(t)=\cos(\omega_g t)$')
plt.xlim(-1,Lg)
plt.ylim(-1.1,1.1)
plt.xlabel('dicrete time in samples $k$')
plt.legend(loc='lower right')

plt.subplot(3,1,3)
plt.plot(gAttack,marker='.',label='$g_{\mathrm{attack}}(t)$')
plt.xlim(-1,Lg)
plt.ylim(-1.1,1.1)
plt.xlabel('dicrete time in samples $k$')
plt.legend(loc='lower right')

# create a second axis to (additionally) show time in ms
ax1 = plt.gca()                   # get current axis
ax2 = ax1.twiny()                 # add a secod axis (allowing for second x-labels) 
ax2.set_xticks(ax1.get_xticks())  # copy x-ticks to second axis
ax2.set_xbound(ax1.get_xbound())  # copy x-bounds to second axis
ax2.set_xticklabels([str(x/fs*1000) for x in ax1.get_xticks()])
ax2.set_xlabel('time $t$ in ms');

plt.tight_layout()

grelease

K=2

Ldecay = np.round(0.15*Lg)        # length of the attach part
print((K-1)/K)
print(np.arccos((K-1)/K))
      
      
tc = tPeak + np.arccos((K-1)/K)/omega_g

print('tPeak='+str(tPeak*1000)+' ms, '+str(tPeak*fs)+'samples')
print('tc=   '+str(tc*1000)+' ms, '+str(tc*fs)+'samples')

t = np.arange(tPeak,tc,dt)         # shorter time vector in seconds

g_decay= K* np.cos(omega_g * (t-tPeak)) -K +1

plt.figure()
plt.plot(tAttack,gAttack,marker='.',c='r',label='$g_{\mathrm{attack}}(t)$')
plt.axvline(x=np.max(tAttack),c='r',ls='--',label='$t_\mathrm{peak}}$')
plt.plot(t,g_decay,marker='.',label='$g_{\mathrm{release}}(t)$')
plt.axvline(x=np.max(tc),c='r',ls='--',label='$t_c$')

plt.legend();

最后

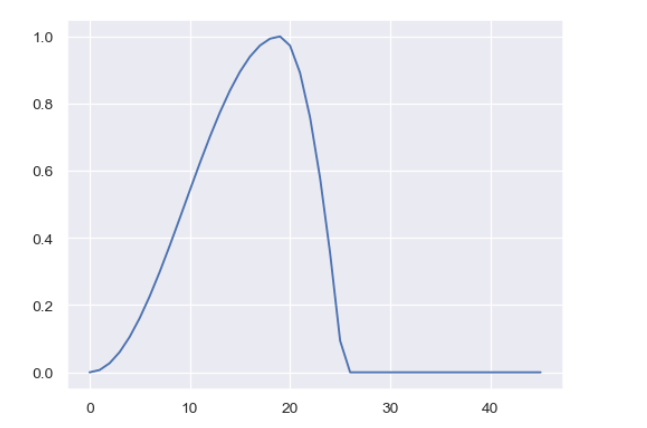
g=np.concatenate((gAttack,g_decay,np.zeros(20,)))

plt.figure()
plt.plot(g);