0 前言
\quad\quad 进化算法是模拟生物自然进化的人工方法,与大自然生态环境一样,进化的物种也需要平衡发展。因此,设计者必须制定合适的生存规则来维持种群的多样性和分布性。在多目标进化算法中,对于某些问题,Pareto最优解集可能很大,也可能包含无穷多个解,把所有这些解都列入到非支配集中有时是比较困难的,同时也没有多少实际意义。因此,有必要使非支配集的大小保持在一个合理的界限内。
\quad\quad 本章将讨论几类比较常用的保持进化群体分布性的方法和技术,如小生境技术、信息嫡 (information entropy) 、 聚集密度 (crowding density)、网格(hyper-grid) 、聚类分析 (clustering analysis)和最小生成树(minimum spaning tree),同时简单讨论非均匀问题的 分布性及其保持策略。
1. 小生境技术
\quad\quad 在生物学上,小生境是在特定环境中的一种组织功能,而将有共同特性的组织称作物种。换言之,生物总是喜欢与自己特征、性状相类似的生物生活在一起,即所谓的 “物以类聚”。在进化算法中,为了保持进化群体的多样性,模拟自然界生物的这种 “物以类聚” 现象, 提出了小生境技术。
目前有代表性的小生境技术主要有以下几种:
\quad\quad ① 基于预选择(preselection)机制的小生境技术(Cavicchio, 1972)。在这种技术中, 只有当子个体的适应度优于其父代个体时,子个体才能替代其父个体,进入下一代进化。 这种相似个体的替代(父个体与子个体之间的性状遗传),能够较好地保持进化群体的多 样性。
\quad\quad ② 基于排挤(crowding)机制的小生境技术(Goldberg et aL 1987) ,这种技术采用群体代间的覆盖方式,依据相似性替代群体中的个体。设置一个排挤因子 C F CF CF ,在进化群体中选取规模为 1 / C F 1/CF 1/CF 的个体组成一个排挤子集,计算新产生的个体与排挤子集中成员之间的相似性。并用新产生的个体替代排挤子集中与其相似的个体。
\quad\quad ③ 基于共享(sharing)机制的小生境技术(Goldberg et al, 1987)。 在这种机制中定义了一个共享函数(sharing function),它表示两个个体之间的相似程度,两个个体越相似, 其共享函数值就越大,反之则越小。一个个体的共享度是该个体与群体中其他个体之间共享函数值的总和。设 d ( i , j ) d(i, j) d(i,j) 为个体 i i i 和 j j j 之间的距离或相似程度(基因型或表现型), S i S_i Si 表示 i i i 个体,在群体中的共享度,则:
S i = ∑ j ∈ P o p n s h [ d ( i , j ) ] S_i = \sum_{j \in Pop}^n sh[d(i, j)] Si=j∈Pop∑nsh[d(i,j)]
\quad\quad 个体 i i i 的共享适应度为 f i t n e s s ( i ) / S i fitness(i)/S_i fitness(i)/Si。其中, P o p Pop Pop 为进化群体, s h [ i , j ] sh[i , j] sh[i,j] 为共享函数, f i t n e s s ( i ) fitness(i) fitness(i) 为个体 i i i 的适应度。
\quad\quad 这种计算个体共享适应度的方法考虑了一个个体与群体中所有其他个体之间的相似程度,时间开销比较大。目前,用得比较多的是设置一个共享半径(亦称小生境半径),只计算共享半径以内个体的相似程度。设个体 i i i 的适应度为 f i t n e s s ( i ) fitness(i) fitness(i), 个体 i i i 的小生境计数为 m i m_i mi 其中
m i = ∑ j ∈ P o p n s h [ d ( i , j ) ] m_i = \sum_{j \in Pop}^n sh[d(i, j)] mi=j∈Pop∑nsh[d(i,j)]
\quad\quad P o p Pop Pop 为当前进化群体, d ( i , j ) d(i, j) d(i,j) 为个体 i i i 和 j j j 之间的距离或称相似程度, s h [ d ] sh[d] sh[d] 为共享函数, s h [ d ] sh[d] sh[d] 的定义如下:
s h [ d ] = { 0 , if d > σ s h a r e 1 − d / σ s h a r e , if d < σ s h a r e sh[d] = \begin{cases} 0, & \text{if $d > \sigma_{share}$ } \\ 1 - d/\sigma_{share}, & \text{if $d < \sigma_{share}$} \\ \end{cases} sh[d]={0,1−d/σshare,if d>σshare if d<σshare
\quad\quad 式中, σ s h a r e \sigma_{share} σshare 为小生镜半径,通常由用户根据 Pareto 最优解集中个体之间的最小期望间距来确定。
\quad\quad 定义 f i t n e s s ( i ) / m i f itness (i)/m_i fitness(i)/mi 为个体 i i i 的共享适应度,此处 m i m_i mi 实质上就是个体 i i i 在小生境中的聚集度。同 一小生境内的个体互相降低对方的共享适应度。个体的聚集程度越高,其共享适应度就被降低得越多。( m i m_i mi 增加, f i t n e s s ( i ) / m i f itness (i)/m_i fitness(i)/mi 便降低)
多目标优化中个体适应度的计算
(1)目标函数组合法

(2)简单支配关系法

(3)复合支配关系法

2. 信息熵
\quad\quad 在比较早期的多目标进化算法中,一般采用小生境技术来保持进化群体的分布性。而信息熵种方法能从宏观上或从整体上反映出进化群体是否具有良好的多样性。
\quad\quad 定义 4.1 \quad 群体 P o p = { X 1 , X 2 , . . . . , X N } Pop=\{X_1, X_2, ...., X_N\} Pop={X1,X2,....,XN} 的规模为 N N N,个体 X i X_i Xi 由 L L L 个基因构成, X i = [ x i ( 1 ) , x i ( 2 ) , . . . , x i ( L ) ] , i ∈ { 1 , 2 , . . . , N } X_i = [x_i^{(1)}, x_i^{(2)}, ..., x_i^{(L)}], i \in \{1, 2, ..., N\} Xi=[xi(1),xi(2),...,xi(L)],i∈{1,2,...,N}, 群体 P o p Pop Pop 中个体均值定义为 X ‾ = { x ‾ ( 1 ) , x ‾ ( 2 ) , . . . , x ‾ ( L ) } \overline{X} = \{\overline x^{(1)}, \overline x^{(2)}, ..., \overline x^{(L)}\} X={x(1),x(2),...,x(L)}, 其中 X ‾ ( j ) = ∑ i = 1 N ( x i ( j ) / N ) \overline{X}^{(j)} = \sum_{i=1}^N (x_i^{(j)}/N) X(j)=∑i=1N(xi(j)/N)(即所有个体相同位置的基因求和取平均),则解群体的方差定义为 D = [ D ( 1 ) , D ( 2 ) , . . . , D ( L ) ] D = [D^{(1)}, D^{(2)},..., D^{(L)}] D=[D(1),D(2),...,D(L)],其中 D ( j ) = ∑ i = 1 N ( x i ( j ) − x ‾ ( j ) ) 2 / N ) , j ∈ { 1 , 2 , . . . , L } {D}^{(j)} = \sum_{i=1}^N (x_i^{(j) } - \overline x^{(j)})^2/N), j \in \{1, 2, ..., L\} D(j)=∑i=1N(xi(j)−x(j))2/N),j∈{1,2,...,L}(同样按照不同个体相同位置的基因进行计算)
\quad\quad 定义 4.2 \quad 若进化群体 P o p Pop Pop 的规模为 N N N, 将它划分为 m m m 个子集 P 1 , P 2 , . . . , P m P_1, P_2, ..., P_m P1,P2,...,Pm,且满足: ∪ p ∈ { P 1 , P 2 , . . . , P m } P = P o p ; ∀ i , j ∈ { 1 , 2 , . . . , m } \cup_{p \in \{P_1, P_2, ..., P_m \}} P = Pop; \forall i, j \in \{1, 2, ..., m\} ∪p∈{P1,P2,...,Pm}P=Pop;∀i,j∈{1,2,...,m} 且 i ≠ j i ≠ j i=j , P i ∩ P j = ∅ P_i \cap P_j = \emptyset Pi∩Pj=∅,(即:所有子集的并集为全集,子集的交集为空集) 则定义解群体的熵为:
E = − ∑ i = 1 m q i l o g ( q i ) E = - \sum_{i=1}^m q_ilog(q_i) E=−i=1∑mqilog(qi)
式中, q i = ∣ P i ∣ / N , ∣ P i ∣ q_i=|P_i|/N, |P_i| qi=∣Pi∣/N,∣Pi∣ 为 P i P_i Pi 的规模大小
\quad\quad 值得说明的是,解群体的方差在一定程度上反映了解群体的空间分布情况。当解群体中所有个体相同 (归为同一个子集) 时,即 m = 1 m=1 m=1 这时熵取最小值 E = 0 E = 0 E=0 ( l o g 1 = 0 ( log1 = 0 (log1=0 ) ;当 m = N m=N m=N 时,熵取最大值 E = l o g ( N ) E = log(N) E=log(N) ( − N l o g ( 1 / N ) ) = l o g ( N ) (-Nlog(1/N)) = log(N) (−Nlog(1/N))=log(N)。 个体在解群体中分布得越均匀,个体多样性越好,则其嫡就越大。对于十进制编码,嫡的最大值为 E D = l o g N ; E^D=logN; ED=logN;对于二进制编码,熵的最大值 E B = I o g ( m i n ( N , 2 L ) ) E^B=Iog(min(N, 2^L)) EB=Iog(min(N,2L))
\quad\quad 对于单目标优化问题,当解群体的方差很小时收敛;对多目标优化问题,当非支配集收敛到 P a r a t o Parato Parato 最优解时,方差和熵都达到较大值。最理想的情况是非支配集中的 N N N 个个体, 并且都均匀分布在 P a r e t o Pareto Pareto 最优边界上,此时其熵达到最大值,同时也会有较大的方差。
\quad\quad 定义 4.2 \quad ∀ X ∈ P o p , P o p \forall X \in Pop, Pop ∀X∈Pop,Pop 为进化群体, ∣ P o p ∣ = N , X = [ x 1 , x 2 , . . . , x L ] , |Pop| = N, X = [x_1,x_2, ..., x_L], ∣Pop∣=N,X=[x1,x2,...,xL], 设 D D D 为一个符号集, ∣ D ∣ = s , x j ∈ D |D| = s, x_j \in D ∣D∣=s,xj∈D,在 D D D 中的取值概率分别为 P = { P j 1 , P j 2 , . . . , P j s } P=\{P_{j1}, P_{j2},..., P_{js}\} P={Pj1,Pj2,...,Pjs},其中 j ∈ { 1 , 2 , . . . , L } j \in \{1, 2, ..., L\} j∈{1,2,...,L},则对应于基因座 j j j 的信息熵定义为 H j ( N ) = − ∑ k = 1 s P j k l o g ( P j k ) H_j(N) = -\sum_{k=1}^s P_{jk}log(P_{jk}) Hj(N)=−∑k=1sPjklog(Pjk), 其中 P j k P_{jk} Pjk 为 D D D 中第 k k k 个符号出现在基因座 j j j 上的概率,即有 P j k = P_{jk} = Pjk= (基因座 j j j 上出现第 k k k 个符号的总数) / N N N。定义群体的平均信息熵为 H = 1 L ∑ j = 1 L H j ( N ) H = \frac{1}{L} \sum_{j=1}^{L} H_j(N) H=L1∑j=1LHj(N)。
\quad\quad 在刻画群体多样性方面,群体的平均信息熵具有与群体熵相同的能力或效果。但在群体进化过程中,群体的熵不容易求取,而群体的平均信息熵则比较容易求取。(定义 4.1 为群体熵,定义 4.2 为群体的平均熵)
3. 聚集密度
\quad\quad 宏观上,进化群体的熵或群体的平均信息熵能够比较好地刻画群体中个体的多样性与分布性,但这种方法缺乏对群体内部个体之间关系的刻画,因此不便于调控群体进化过程中的多样性与分布性。刻画群体多样性的另一种方法是群体中个体的聚集密度或聚集距离,如果个体之间的聚集距离比较大,则表明个体的聚集密度比较小。这种方法的计算复杂性高于前 一种方法,但它既能从宏观上刻画群体的多样性与分布性,同时也比较好地刻画了个体之间的内在关系,可以用于进化过程中对群体的调控。
\quad\quad 这里介绍三类方法,一类是通过直接计算个体之间的相似度来计算一个个体的聚集密度;第二类是通过计算个体之间的影响因子来计算个体的聚集密度;第三类是通过计算个体之间的聚集距离来计算个体之间的聚集密度。
1. 用相似度来计算个体的聚集密度
\quad\quad 定义 4.4 \quad 群体 P o p = { X 1 , X 2 , . . . . , X N } Pop=\{X_1, X_2, ...., X_N\} Pop={X1,X2,....,XN} 中的个体 X i = [ x i ( 1 ) , x i ( 2 ) , . . . , x i ( L ) ] , X j = [ x j ( 1 ) , x j ( 2 ) , . . . , x j ( L ) ] X_i = [x_i^{(1)}, x_i^{(2)}, ..., x_i^{(L)}],X_j = [x_j^{(1)}, x_j^{(2)}, ..., x_j^{(L)}] Xi=[xi(1),xi(2),...,xi(L)],Xj=[xj(1),xj(2),...,xj(L)] ,定义个体 X i X_i Xi 和个体 X j X_j Xj 之间的相异程度为 A i , j = 1 L ∑ k = 1 L C k ( x i ( k ) − x j ( k ) ) A_{i, j} = \frac{1}{L} \sum_{k=1}^{L} C_k(x_i^{(k)} - x_j^{(k)}) Ai,j=L1∑k=1LCk(xi(k)−xj(k)),其中 i , j ∈ { 1 , 2 , . . . , N } , i, j \in \{1, 2, ..., N\}, i,j∈{1,2,...,N}, C k C_k Ck 为对应于基因座 k k k 的常数因子, 且通常有 C k = B C ( k + 1 ) , B C_k=BC_{(k+1)}, B Ck=BC(k+1),B 为一常量。定义个体 X i X_i Xi 和个体 X j X_j Xj 之间的相似度为 1 − A i , j 1-A_{i, j} 1−Ai,j。
\quad\quad 定义 4.5 \quad 定义个体 p p p 的聚集度为与个体 p p p 相似的个体在群体中所占比重,即 c r o w d s ( p ) crowds(p) crowds(p) 与个体 p p p 相似度大于 γ \gamma γ 的个体的总数 / N /N /N 其中 γ \gamma γ 为一常数,一般取值为 γ ∈ [ 0.9 , 1 ] \gamma \in [0.9, 1] γ∈[0.9,1] 。
2. 用影响因子来计算个体的聚集密度???

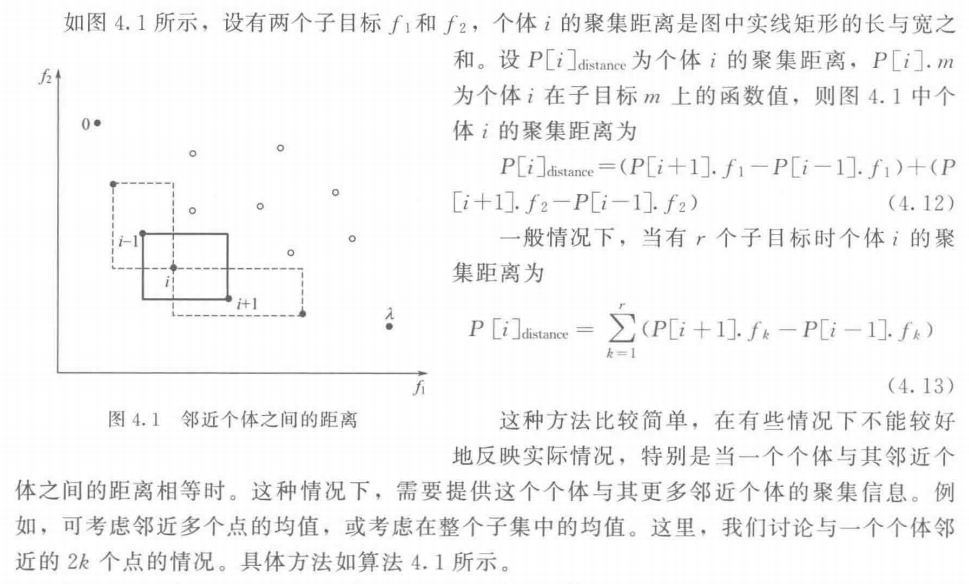
3. 用聚集距离来计算个体的聚集密度

4. 网格
\quad\quad 网格方法以不同的方式被多个 MOEA 设计者用于保持进化群体的分布性,如 PESA (Corne et al, 2000)、PAES ( Knowles et al, 2000)、MGAMOO (Coello Coello et al, 2001),以及 EMOEA (郑金华,2005)下面具体讨论网格方法,如网格的边界、个体在网格中的定位,以及自适应网格等。
1. 网格边界

2. 个体在网格中的定位

3. 自适应网格

5. 聚类方法
5.1 聚类分析中的编码及其相似度计算

(1)实数编码及其相异度计算

(2) 二进制串编码及其相似度计算

(3) 树结构编码及其相似度计算


(4) 符号编码及其相似度计算

(5) 混合编码及其相似度计算

5.2 聚类分析
\quad\quad 在多目标进化算法中,聚类分析的目的是为了维持和增强进化群体的多样性与分布性,聚类分析的方法主要有划分法、层次法、基于密度的方法、基于网格的方法和基于模型的方法等。在实际应用中,这些方法通常不是单独出现的,而是多种方法的相互结合。本小节只讨论基于中心点的聚类算法和基于层次凝聚距离的聚类算法
(1)基于中心点的聚类算法

(2)基于类距离的层次聚类算法



5.2 极点分析与处理

6. 非均匀问题的分布性
\quad\quad 在讨论多目标进化算法的分布性时,通常只考虑了均匀分布的情况。而在实际应用中, 可能存在非均匀分布的情况。如何维护非均匀分布优化问题的分布性是一个极具挑战的研究课题。Fonseca 等于 1995 年首次提到了非均匀分布的概念(Fonseca et al, 1995),Deb 提出了构造非均匀测试函数的方法,并构造了两个非均匀测试函数 (Deb, 1999),Pedersen 等根据决策者的需要把解集的分布分为均匀和非均匀两种情况,但只讨论了前者(Pedersen cl al, 2004)。Fieldsend 等较详细地分析了非均匀分布情况,强调了决策者偏好的重要性 (Fieldsend et al, 2004)
\quad\quad 本节讨论李密青和郑金华等提出的一种非均匀分布问题分布性维护方法,该方法定义一个反映个体分布“规则”程度的指标:杂乱度,并设计一种降低种群杂乱度的方法,在未知 Pareto 最优面分布规律的情况下有效剔除造成种群混乱的个体。
6.1 非均匀分布问题
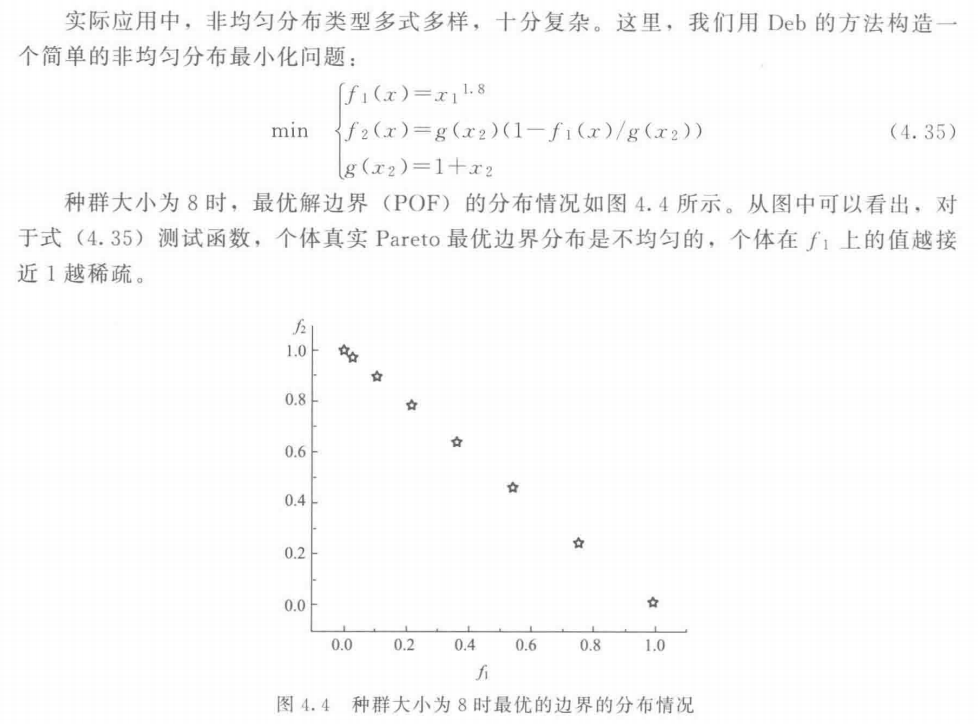
6.2 杂乱度分析
\quad\quad
定义4.9
\quad
对种群
P
P
P 生成一棵欧氏最小生成树(euclidean minimum spanning tree,EMST),对于
P
P
P 的任一个体
i
i
i 定义,杂乱度
m
e
s
s
y
i
messy_i
messyi 为
m
e
s
s
y
i
=
l
i
_
m
a
x
/
l
i
_
m
i
n
−
1
/
d
i
messy_i = l_{i\_max}/l_{i\_min} - 1/d_i
messyi=li_max/li_min−1/di
式中,
d
i
d_i
di 为个体
i
i
i 在
E
M
S
T
EMST
EMST 中的度数;
l
i
_
m
a
x
、
l
i
_
m
i
n
l_{i\_max}、l_{i\_min}
li_max、li_min 分别为
E
M
S
T
EMST
EMST 中连接
i
i
i 的最长边和最短边。个体杂乱度由边长之比和个体度数两部分组成,边长之比越大,度数越高,杂乱度越大。
\quad\quad 由 E M S T EMST EMST 的贪婪性和连通性可知, E M S T EMST EMST 中的边实质是连接不同聚类之间的最短距离(单个个体也可以看作一个聚类),即种群由 E M S T EMST EMST 中任意一边划分的两个个体集(聚类)之间,不存在比该边更短的距离。这样, E M S T EMST EMST 中具有两个以上边的个体(即度数大于等于 2 的个体)可以看作连接不同聚类的中间个体,边的长度可以看作个体与聚类之间的距离。自然地,个体最大边与最小边的比反映了个体与不同聚类之间距离的最大差异,比值大表明了个体与周围不同聚类的 “联系” 参差不齐,相对混乱。另外,对于 E M S T EMST EMST中度数为 1 的个体,它们的最大边与最小边相同。这些个体只与一个聚类连接, 没有反映个体与不同聚类之间联系的差异,我们赋予它较小的杂乱度。此外,个体在 E M S T EMST EMST 中的度数也在一定程度上反映了个体的位置关系,通常边界个体具有较低的度数, 这样在边长之比相近但分布位置不同的个体之间,边界个体具有更低的杂乱度。下面讨论用个体杂乱度对种群进行维护。
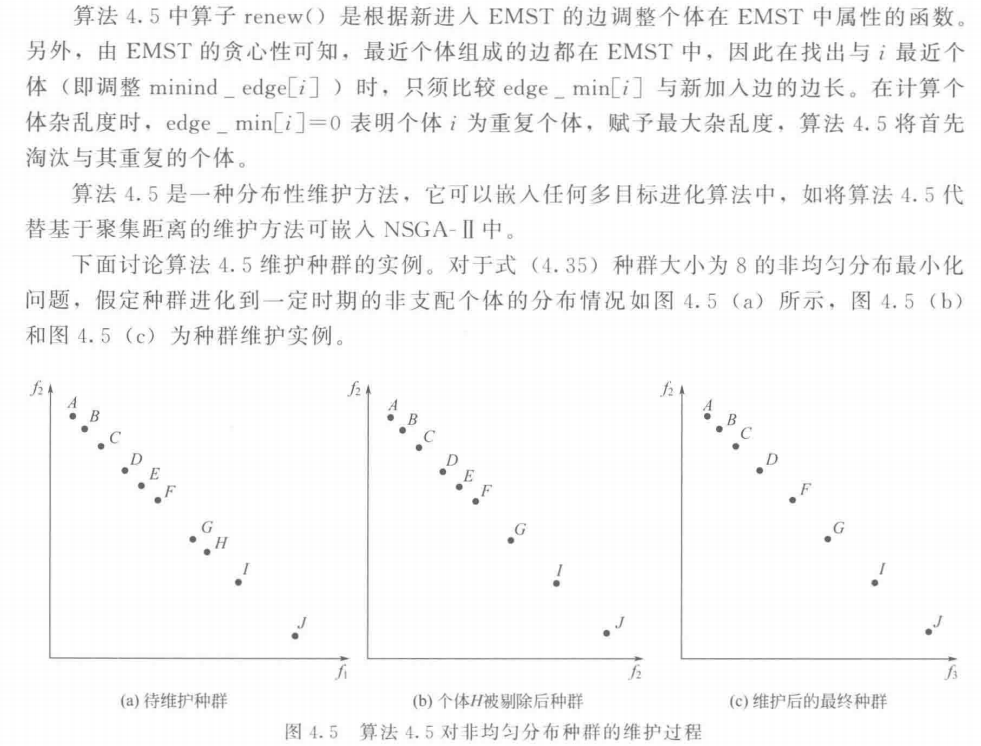
6.3 种群维护





![[论文阅读] 颜色迁移-N维pdf迁移](https://img-blog.csdnimg.cn/06c6c2e5b26248b6affad1f1aaee0471.png)