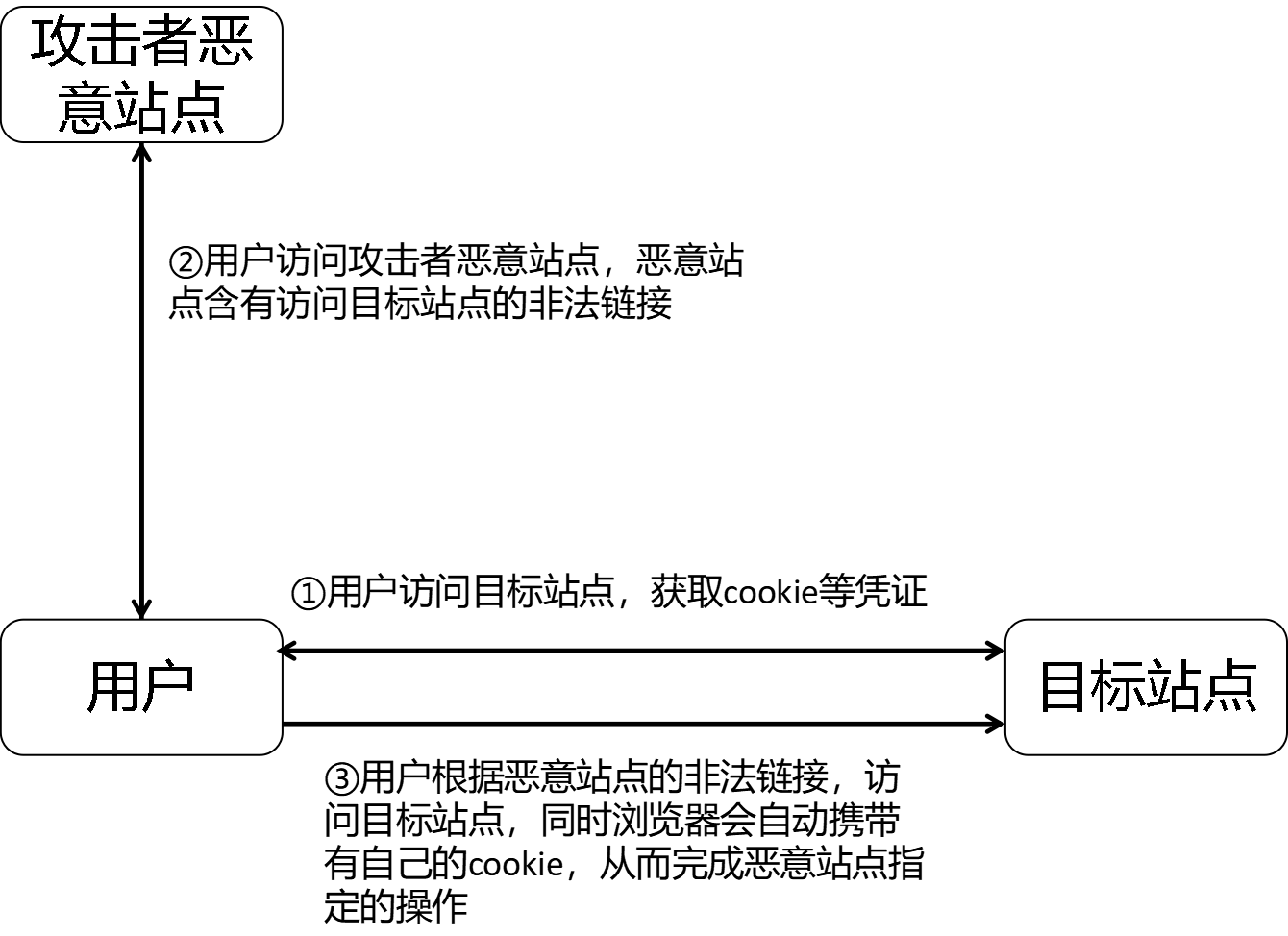
为论述概率模型的思想，本部分以下图所描述的情况作为例子讲述，为简化图省略线路开关。

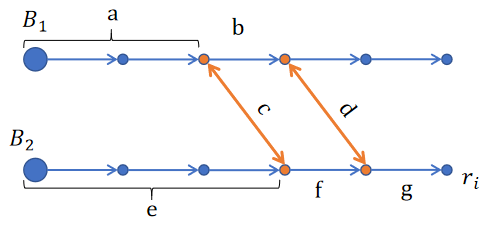
不同于单供网络，双供网络由于多条联络线，存在多个扩展供电方案。设供电路径$P=(p_1,p_2,..,p_n)$，其中$p_i$为子路径。用字母$a-g$表示子路径的可靠性（为了方便表达有时可指代路径本身），如字母$a$表示从电源出发一直到首个联络点（不包含该联络点）之间路径的可靠性。假设目前需求解最右下角节点$i$的可靠性$r_i$，观察到存在$(a,c,f,g)$和$(a,b,d,g)$，两条条电源$B_1$扩展供电路径，以及原先单供网络电源$B_2$的供电路径$(e,f,g)$，容易得到每条路径的可靠性：

$r_1=r(a,c,f,g)=acfg$，$r_2=r(a,b,d,g)=abdg$，$r_3=r(e,f,g)=efg$

由于路径相互重叠，它们之间的可靠性不是相互独立的，如$r((a,c,f,g)\cap (a,b,d,g))\ne r(a,c,f,g)\times r(a,b,d,g)$，但可以用两条路径包含的所有子路径可靠性之积表达，子路径之间是相互独立的！

$r((a,c,f,g)\cap (a,b,d,g))={\prod }_{p\in (a,c,f,g)\cup (a,b,d,g)}r(p)=acfgbd$

进一步，可通过容斥原理计算存在$(a,c,f,g)$和$(a,b,d,g)$两条供电线路时的节点的可靠性$r_{12}$：

$r_{12}=r((a,c,f,g)\cup (a,b,d,g))=r(a,c,f,g)+r(a,b,d,g)-r((a,c,f,g)\cap (a,b,d,g))=ag\times (bd+cf-bdcf)$

同理，$r_{13}=g\times (abd+ef-abdef)$，$r_{23}=fg\times (ac+e-ace)$

这里没有通过事件以及发生概率规范表述，特此补充。路径$(a,c,f,g)$和$(a,b,d,g)$其中之一可靠的事件发生概率为$r((a,c,f,g)\cup (a,b,d,g))$，即目标节点的用电可靠性，路径$(a,c,f,g)$和$(a,b,d,g)$同时可靠的事件发生概率为$r((a,c,f,g)\cap (a,b,d,g))$.

进而3条供电路径可根据3元容斥原理计算$r_i$：

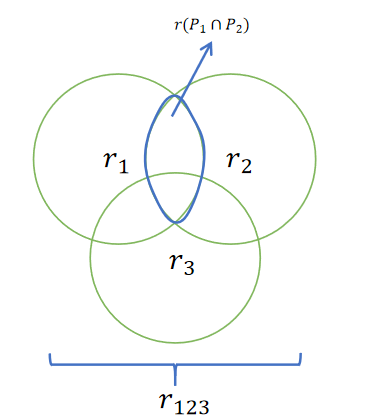
$r_i=r_{123}=acfg+abdg+efg-acfgbd-acfge-abdgef+abcdefg$

以上讨论，可进一步拓展至$n$条供电路径的情况。设对于目标供电节点$i$，存在供电路径集合 P = { P 1 , P 2 , . . . , P n } P=\{P_1,P_2,...,P_n\} P={P1​,P2​,...,Pn​}，现求节点$i$的用电可靠性$r_i$。相应地，应用$n$元容斥原理：

$r_i=r(P_1\cup P_2\cup ...\cup P_n)=\sum r(P_i)-\sum r(P_i\cap P_j)+\sum r(P_i\cap P_j\cap P_k)-...+(-1{)}^{n-1}r(P_1\cap P_2\cap ...\cap P_n)$

设 a i ∈ { 1 , 2 , . . . , n } a_i\in\{1,2,...,n\} ai​∈{1,2,...,n}且$\forall i\ne j$，有$a_i\ne a_j$，则$m(m\le n)$条供电路径 { P a 1 , P a 2 , . . . , P a m } \{{P_{a_1}},{P_{a_2},...,{P_{a_m}}}\} {Pa1​​,Pa2​​,...,Pam​​}同时可靠的概率描述为

r ( P a 1 ∩ P a 2 ∩ . . . ∩ P a m ) = ∏ p ∈ { P a i ∣ i = 1 , 2 , . . . , m } r ( p ) r(P_{a_1}\cap P_{a_2}\cap...\cap P_{a_m})=\prod_{p\in \{P_{a_i}|i=1,2,...,m\}}r(p) r(Pa1​​∩Pa2​​∩...∩Pam​​)=∏p∈{Pai​​∣i=1,2,...,m}​r(p)

其中 p ∈ { P a i ∣ i = 1 , 2 , . . . , m } p\in \{P_{a_i}|i=1,2,...,m\} p∈{Pai​​∣i=1,2,...,m}为最小子路径，相互独立。