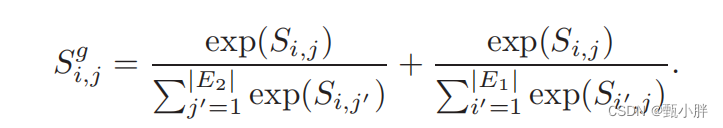[论文阅读] 颜色迁移-N维pdf迁移
文章: N-Dimensional Probability Density Function Transfer and its Application to Colour Transfer, [paper ][code]
1-算法原理
简单来说, 本文将图像看作是随机变量的一组样本, 图像之间的颜色迁移可以看作是样本之间分布的迁移. 因而本文的方法就是寻找样本分布之间的迁移方法.
如下图所示为文中给出的2d pdf迁移方法的示例.
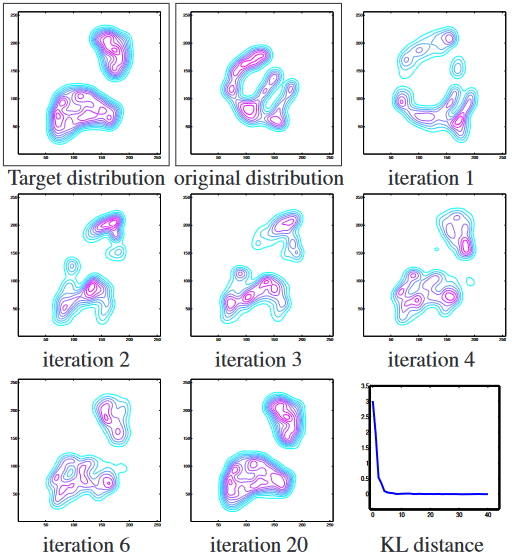
具体的, 本文算法步骤如下所示:

下面就我个人理解进行说明下:
- 第一步是初始化, 可以看到, 本文是在rgb空间进行处理的, 且是使用迭代的方法, 因而处理过程中x是不断变化的
- 第二大步是算法核心, 算法迭代, 查找映射关系, 具体的
- 使用旋转矩阵R对样本x和y进行处理, 将其变换到新的坐标系, 对应上图中的步骤3
- 在新的坐标系, 对每个轴寻找1维的pdf映射, 对应上图中的步骤5
- 对图像进行映射, 得到当前步骤处理后的图像, 对应上图中的步骤6
- 处理完后, 映射回原始坐标系, 对应上图中的步骤7
- 重复步骤2-5, 得到最终的图像.
2-算法核心
本文的目的是N维pdf的迁移, 但对于高维的pdf迁移是比较困难的, 因而本文将其转换为1维的迁移. 因此本文有2个方面的问题需要解决: 一是1维pdf如何迁移; 二是如何转换为1维pdf.
2.1-1D pdf transfer
本文介绍了一种方法, 如下所示, Cx 和 Cy 分别为累积概率分布函数.
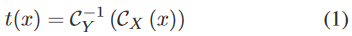
这种方法是 Digital Image Processing 书中的方法, 我觉得有点类似直方图均衡或者直方图规定化(直方图匹配).
代码中给出的实现是使用插值算法实现的, 作者给出的实现是使用matlab的, 其中PX为原始图像某个轴的累积概率分布, PY为目标图像某个轴的累积概率分布
f = interp1(PY, 0:nbins-1, PX, 'linear');
2.2-rotation matrix R
本文使用旋转矩阵R将原始样本变换到新的坐标系, 然后对新坐标系的每个轴进行1d transfer. 之所有要使用旋转矩阵, 个人以为的原因是(可能并不准确):
- 样本分布比较复杂, 原始坐标系(RGB空间)中的迁移不能实现准确的pdf匹配
- pdf的迁移存在大量非线性处理, 原始坐标系(RGB空间)可能不足以表达
- 原始坐标系变换, 拉伸幅度可能过大, 导致图像颜色异常, 变换到新的高维坐标系后, 每个轴的变化变小, 可以减少拉伸幅度
因而旋转矩阵R的选择比较关键, 文中测试了几种R的选择方法, 最后发现使用随机的方法, 效果最好, 如下所示:
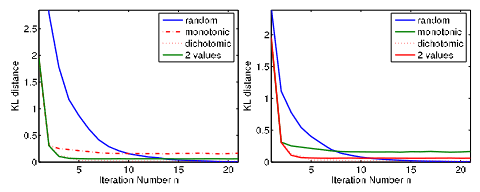
旋转矩阵R的大小为 m*3, 根据文章中的说法, m越大pdf匹配越精确, 但速度也越慢. 代码中给出的实现使用m=6, 如下所示.
R{1} = [1 0 0; 0 1 0; 0 0 1; 2/3 2/3 -1/3; 2/3 -1/3 2/3; -1/3 2/3 2/3];
for i=2:nb_iterations
R{i} = R{1} * orth(randn(3,3));
end
这里没有看懂, 直接给R随机赋值不行吗?
3-算法效果
如下图所示为文章中给出的效果.