5.1.概述
二叉搜索树,也叫二叉查找树、二叉排序树,顾名思义,这种二叉树是专门用来进行数据查找的二叉树。二叉搜索树的查找其实就是二分查找。
二叉搜索树的定义:
- 二叉搜索树可以为空
- 如果二叉搜索树不为空,那么每个有孩子结点的结点,其左孩子的值一定要小于它,其右孩子的值一定要大于它。
二叉搜索树的操作集:
既然是专门用来进行查找的二叉搜索树的操作集自然就是增删查,没有改,因为二叉搜索树中的元素都是排序好的,如果直接就地改动某个节点很可能破坏有序性,所以当发现插入的数据有误的时候先删除,再重新插入,一定要保证数据经过了插入流程,这样数据才会在对的位置,才能保证整棵的有序性。
boolean find(Object target);
Object findMin();
Object findMax();
void insert(Object data);
void delete(Object data);5.2.操作
5.2.1.节点
节点实体如下:
public class Node {
//数据域
private int data;
//指针域
private Node left;
private Node right;
//遍历标志
private boolean isOrder;
{
isOrder=false;
}
public Node(){
}
public Node(int data){
this.data=data;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
public boolean isOrder() {
return isOrder;
}
public void setOrder(boolean order) {
isOrder = order;
}
}5.2.2.插入
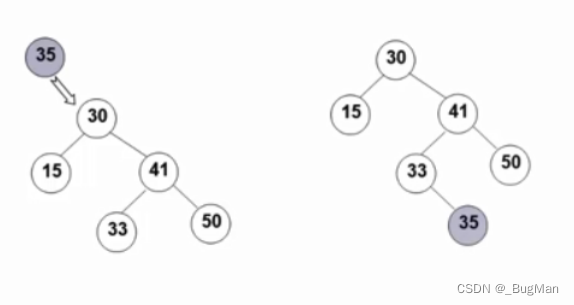
假设插入35,从根节点开始比较,
35>30,属于30的右子树,30的右孩子不为空,继续向下走,
35<41,属于41的左子树,41的左孩子不为空,继续向下走,
35>33,属于33的右子树。33的右孩子为空,35是33的右孩子。
代码示例:
//记录根节点
private static Node root=null;
//用于寻路的指针
private static Node flag=null;
public static void insert(Node node){
if(root==null){
System.out.println("我插入"+node.getData()+"作为根节点");
root=node;
}
flag=root;
while (node.getData()<flag.getData()){
if(flag.getLeft()==null) {
System.out.println("我在"+flag.getData()+"右边插入一个"+node.getData());
flag.setLeft(node);
}
flag = flag.getLeft();
}
while(node.getData()>flag.getData()){
if(flag.getRight()==null) {
System.out.println("我在"+flag.getData()+"右边插入一个"+node.getData());
flag.setRight(node);
}
flag = flag.getRight();
}
}5.2.3.查找
1.查找某个值是否存在
二叉搜索树的查找其实就是借助数据结构实现了二分查找,如果当前节点的值大于要查找的值,说明要查找的值只可能存在于当前节点的右子树,如果当前节点的值小于要查找的值,说明要查找的值只可能存在于当前节点的左子树。不断重复以上过程,遇见两种情况终止:
- 当前节点是要查找的值,查找成功,说明值存在。
- 当前的值不是要查找的值,且节点没有左右子树,是叶子节点,查找失败,说明值不存在。
代码示例:
public static boolean find(int target){
//从根节点开始
flag=root;
while(true){
//当前节点值为查找值
if(flag.getData()==target){
return true;
}
//向右子树查找
if(target>flag.getData()){
flag=flag.getRight();
}
//向左子树查找
if(target<flag.getData()){
flag=flag.getLeft();
}
//当前节点是叶节点
if(flag==null){
return false;
}
}
}2.查找最大值
从根节点开始一直沿着右子树的右孩子进行查找,右子树的最后一个右孩子一定是最大值。
public static int findMax(){
flag=root;
while(flag.getRight()!=null){
flag=flag.getRight();
}
return flag.getData();
}3.查找最小值
从根节点开始一直沿着左子树的左孩子进行查找,左子树的最后一个左孩子一定是最小值。
public static int findMin() {
flag = root;
while (flag.getLeft() != null) {
flag = flag.getLeft();
}
return flag.getData();
}5.2.4.删除
被删除的节点有三种情况:
- 叶子节点,直接删除即可。
- 只有一个孩子,用孩子节点接替被删除节点即可。
- 左右孩子双全,用左子树中最大值接替被删除节点,用右子树中最小值接替被删除节点。
代码示例:
二叉搜索树由于是整体有序的,每个元素的变动都会造成一定范围内需要进行整体的重新排序,且排序过程是重复的,因此这个过程用递归实现更加简洁,用循环会很冗长,此处选用递归实现。
public static void delete(int target){
flag=root;
//由于删除节点会引起树的调整,为了以防万一根节点需要重新指向一下
root=doDelete(flag,target);
}
private static Node doDelete(Node node,int target){
//空树直接返回,或者是递归出口1:已经遍历完整棵树
if(node == null) {
return null;
}
//递归左子树
if(target < node.getData()) {
node.setLeft(doDelete(node.getLeft(), target));
}
//递归右子树
if(target > node.getData()) {
node.setRight(doDelete(node.getRight(), target));
}
//执行到此步,说明已经出递归,并且没有走递归出口1返回,说明找到了目标
//情况1:被删除节点只有一个孩子节点
//情况2:被删除节点为叶子节点
//以上两种情况可以合并成一个逻辑处理,即指向自己的孩子节点即可
if(node.getLeft() == null) {
return node.getRight();
}
if(node.getRight() == null) {
return node.getLeft();
}
//情况3:被删除节点左右孩子双全,找右子树中最小值接替被删除节点,右子树需递归此过程整体做调整
Node minNode = findMinNode(node.getRight());
node.setData(minNode.getData());
node.setRight(doDelete(node.getRight(),minNode.getData()));
return node;
}
private static Node findMinNode(Node node){
while(node.getLeft() != null)
node = node.getLeft();
return node;
}