导读	Linux Mint 的更新管理器变得更有用了！

Linux Mint 的更新管理器是该发行版的一个重要组成部分，它使新用户可以获得更为方便简易的体验。

最近的一次更新 Linux Mint 21 推出了许多改进，包括更新管理器对 Flatpak 的支持。

你只需要更新你的系统就可以获得这些改进。

更新管理器中支持 Flatpak

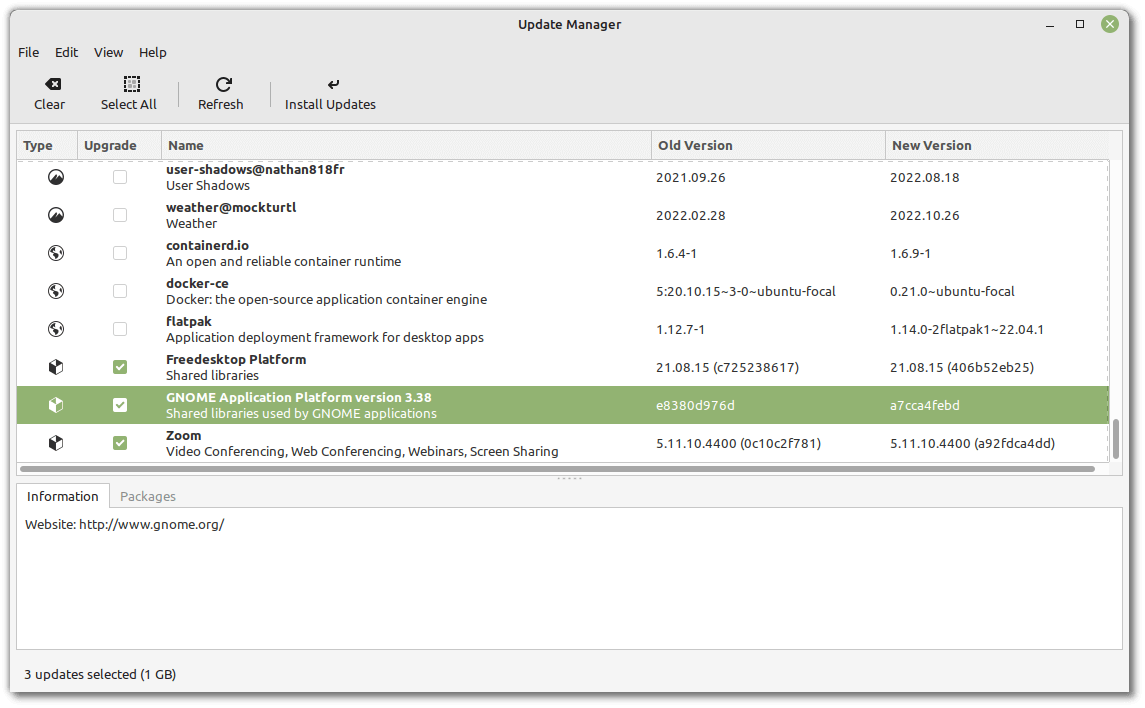
是的，你没看错。这终于实现了。

Flatpak 支持已被添加到更新管理器中，用户只需单击几下就能更新 Flatpak 应用程序和运行时。

这将为进一步改善用户体验的统一更新体验提供了帮助。

这对新用户来说很有好处，他们不需要熟悉终端命令就能更新 Flatpak。此外，你不需要将 Flatpak 与软件中心集成（对于 GNOME 而言）。

换句话说，Linux Mint 团队增强了你使用 Flatpak 应用程序的体验。

除了对 Flatpak 的支持，本次更新还包括对 Linux Mint 21 的更多增强，这是一个开箱即用的更新。

这些改进包括：

对角栏的改进

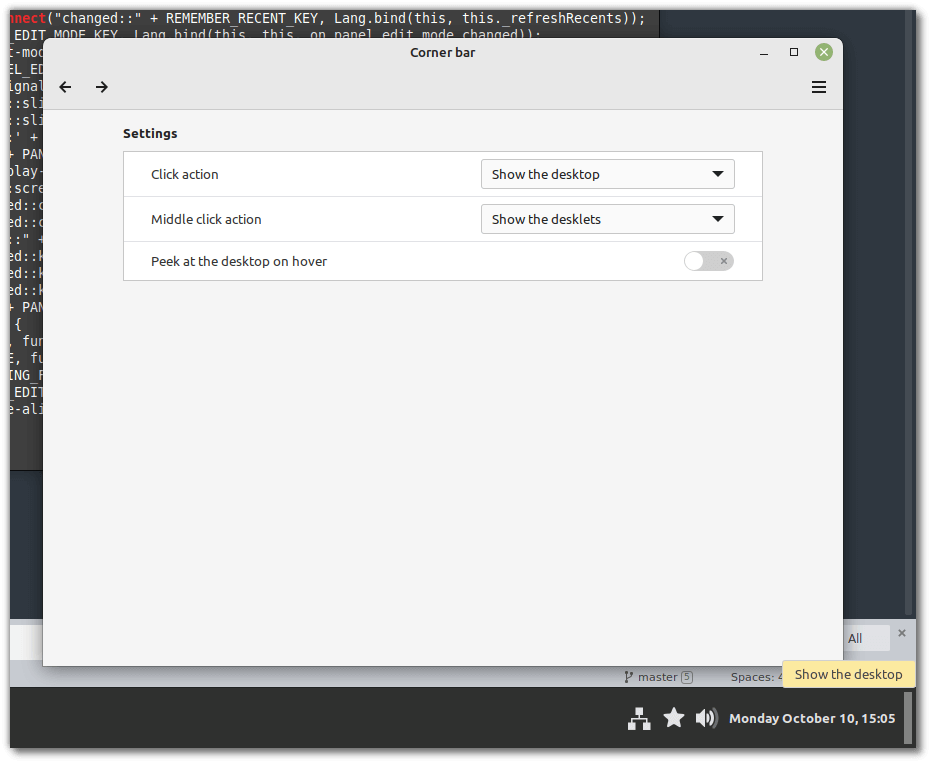
Linux Mint 21 中的 角栏Corner Bar 添加了两项新特性：

能够在角栏设置左键点击和中键点击的动作；你可以配置它以显示桌面、工作区选择器或桌面。
一个允许你将鼠标悬停在角栏上以显示桌面的新选项。

Nemo 的更新

Nemo 文件管理器做了一些调整；现在，当文件被选中时，只会高亮显示文件名，而不是图标和文件名。

如果你还不知道, 你也可以通过我们建议的一些调整来增强 Nemo 文件管理器的体验：

调整 Linux 中的 Nemo 文件管理器，让它更好用的 15 种方法

此外，桌面图标被垂直翻转，桌面上下文菜单中添加了一个新的快捷方式，可以快速打开显示设置。

更少的密码提示

这是很多人可能喜欢的另一个用户体验调整。

当删除 Flatpak 或任何快捷方式或本地应用程序时，它将不再要求你输入密码。

类似地，在新立得（LCTT 译注：Linux 下的一个包管理工具）和更新管理器的情况下，将使用 pkexec 来记住密码。

这样，用户就不需要每次执行多个操作时都输入密码。

你可以浏览 Linux Mint 月度博客 以了解其它变化。更多Linux资讯请查看：https://www.linuxprobe.com