目录
- 时间复杂度
- 选择排序
- 冒泡排序
- 异或交换
- 解释
- 案例
- 综上
- 插入排序
- 二分查找
- 拓展
- 对数器
时间复杂度
- 如果一个操作时间和数据量没有关系,则是常数时间的操作
- 比如一个数组arr[n]这就是算一个偏移量,然后找到这个位置的值,这就是常数时间,和数组长度没有关系。
- 而对于链表list.get(n),这就需要进行遍历直到找到n,这就和数据量有关系了。
这里举个选择排序的例子说明一下时间复杂度
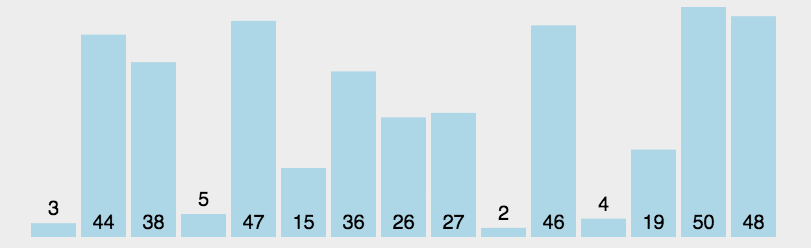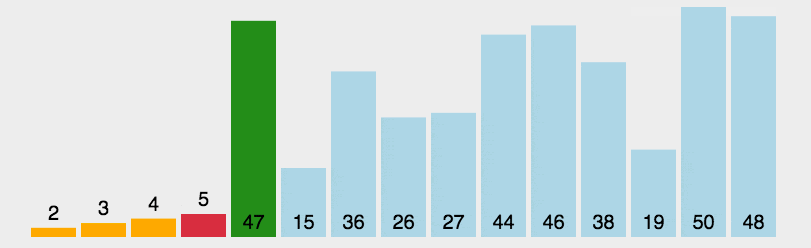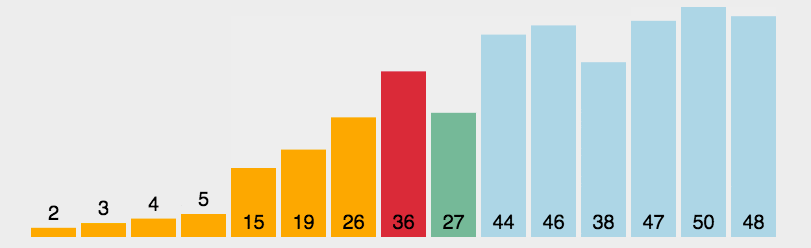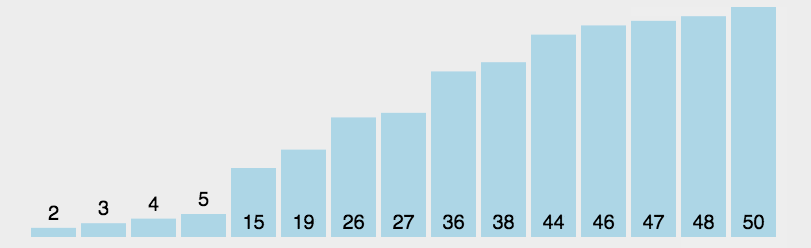
- 第一次循环确定最小值
- 遍历n次,对比n-1次,交换1次
- 第二次循环确定最小值
- 遍历n-1次,对比n-2次,交换1次
- 第三次循环确定最小值
- 遍历n-2次,对比n-3次,交换1次
······
- 第N次循环确定最小值
- 遍历1次,对比0次,交换0次
把所有操作次数相加(n+n-1+n-2·····)+(n-1+n-2+····)+(1+1+1····)
算出来结果(系数就不细算了):an2+bn+1
取最高次项n2,所以时间复杂度为O(n2)说明:还有最优时间复杂度和平均时间复杂度,但我们日常提及的都是最坏时间复杂度
选择排序
时间复杂度O(n2);空间复杂度O(1);
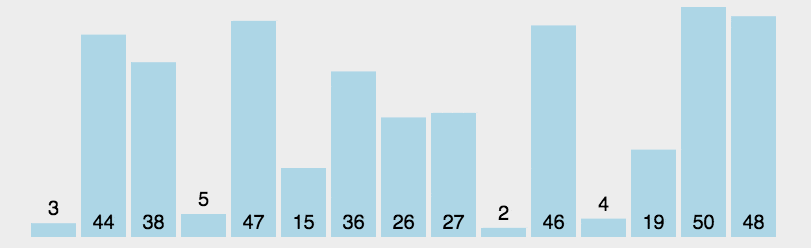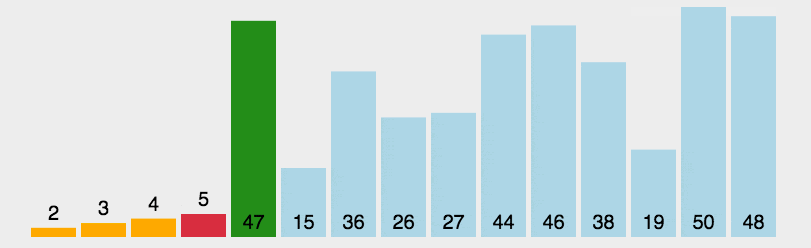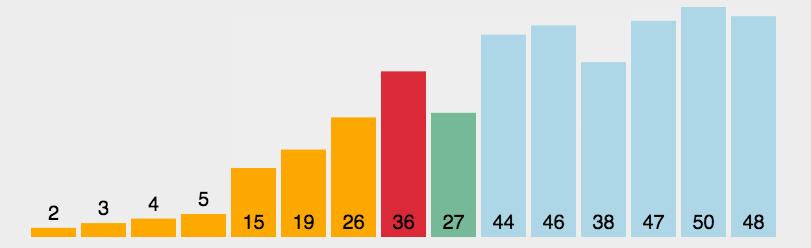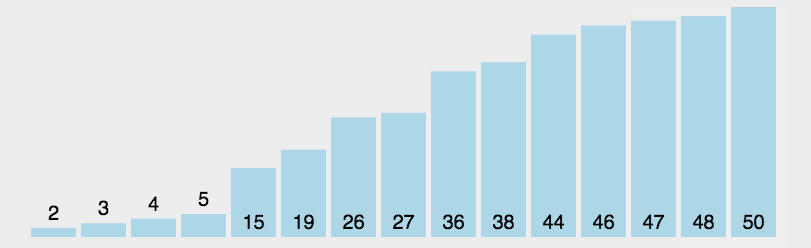
public class SelectionSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
// 总共要经过 N-1 轮比较
for (int i = 0; i < arr.length - 1; i++) {
int min = i;
// 每轮需要比较的次数 N-i
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
// 记录目前能找到的最小值元素的下标
min = j;
}
}
// 将找到的最小值和i位置所在的值进行交换
if (i != min) {
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
return arr;
}
}
冒泡排序
时间复杂度O(n2);空间复杂度O(1);
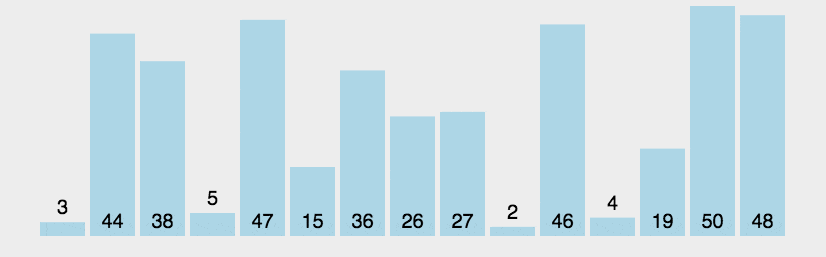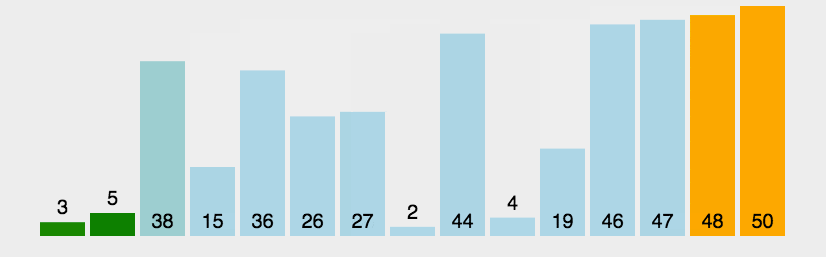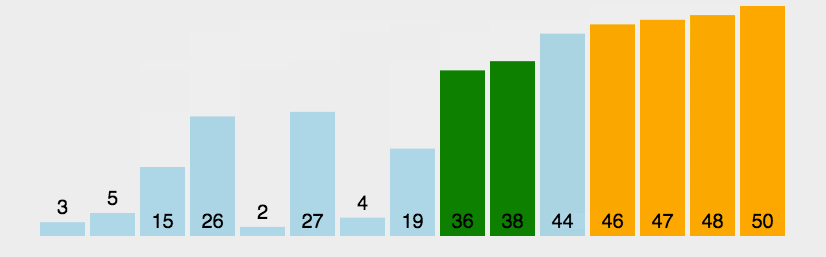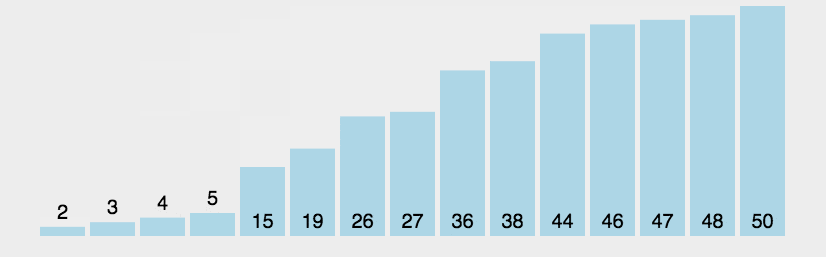
public class BubbleSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
for (int i = 1; i < arr.length; i++) {
// 设定一个标记,若为true,则表示此次循环没有进行交换,也就是待排序列已经有序,排序已经完成。
boolean flag = true;
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flag = false;
}
}
if (flag) {
break;
}
}
return arr;
}
}
异或交换
解释
1^1=0; 0^0=0; 1^0=1,满足交换律结合律 所以自己和自己异或就为0;有点像消消乐,出现两次就消除。 这里有两个变量a,b(所占内存不相交),如何利用异或进行交换a = a^b;
b = a^b;
a = a^b;即可实现交换,但前提是这两个变量所占内存不相交,也就是相互不影响。
案例
- 一个数组,里面只有一种数字出现奇数次,其余数字皆出现偶数次,求出这个出现基数次的数字
分析出现偶数次,那异或就全都消失了。所以每一项进行异或,偶数次都会消失,剩下的就是出现奇数次的数字了。
- 一个数组,里面只有两种数字(不同)出现奇数次,其余数字皆出现偶数次,求出这个出现基数次的数字
每一项进行异或,偶数次都会消失,剩下的就是两个奇数次的数字相异或的结果了记为c。既然这两个数字不同,那异或就一定不为0,那我们找到这两个数字不同的地方,比如得到的结果0100,所以说明第三位这两个数字不同,那我们找做一个循环,重新遍历一下数组,第三位为1的(0的)进行异或,得到的结果就是其中一个数字记为a,剩下的数字,只需要a^c即可得到。
- 这里遍历的时候怎么判断某一位为1或者0呢?
- 我们选择最低位的不同数字,取反加一与:c&(~c+1)
- 比如c=10011010,则~c+1=01100110;两个相与得到的就是00000010
- 然后遍历看谁00000010相与不为0,或为0,则为两种情况
综上
异或可以得到群体中落单的那数字
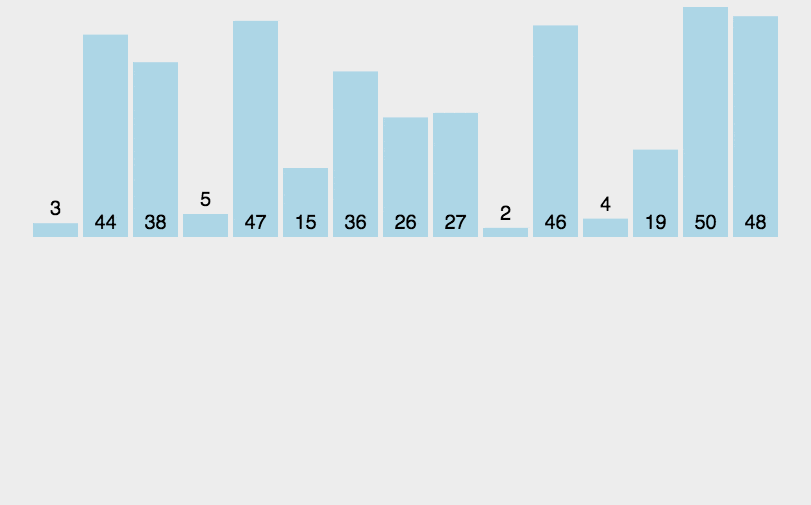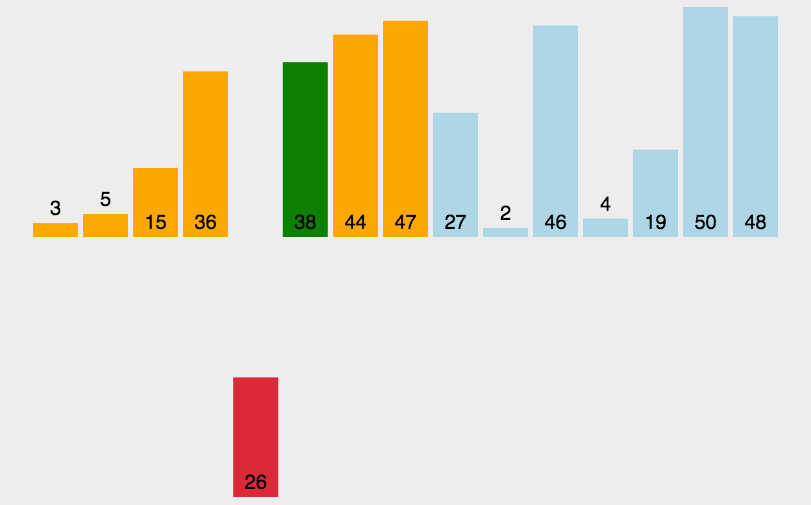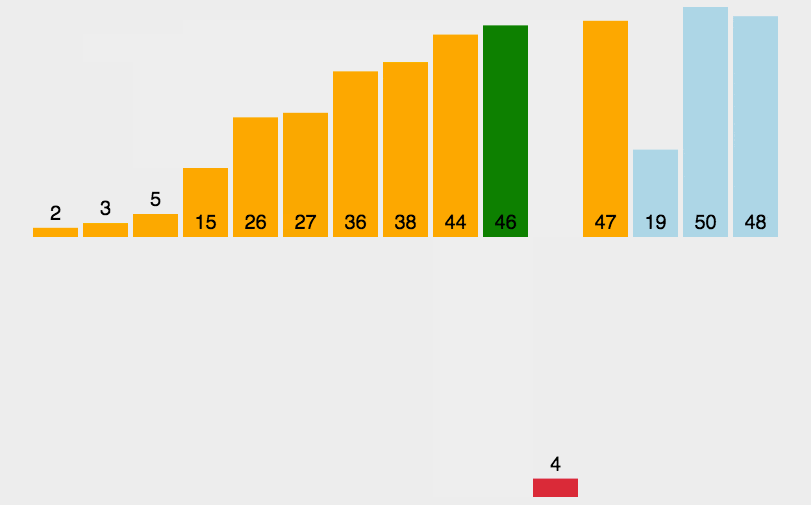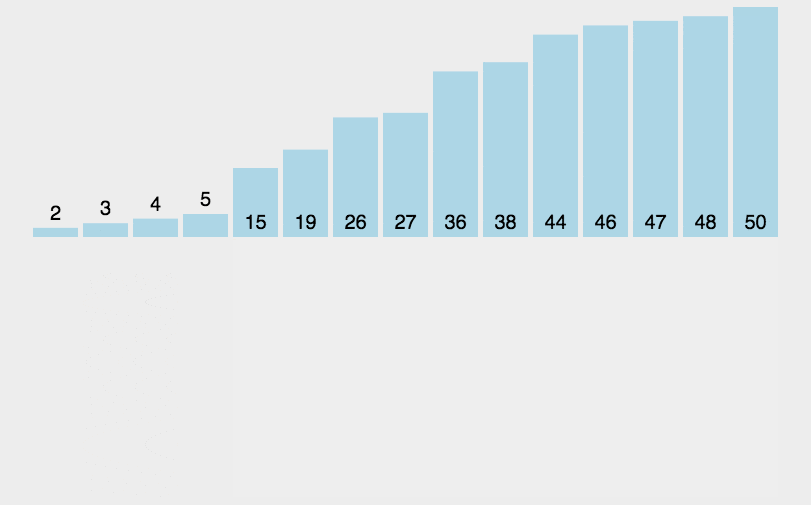
插入排序
时间复杂度:O(n2),空间复杂度:O(1)
public class InsertSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
// 从下标为1的元素开始选择合适的位置插入,因为下标为0的只有一个元素,默认是有序的
for (int i = 1; i < arr.length; i++) {
// 记录要插入的数据
int tmp = arr[i];
// 从已经排序的序列最右边的开始比较,找到比其小的数
int j = i;
while (j > 0 && tmp < arr[j - 1]) {
arr[j] = arr[j - 1];
j--;
}
// 存在比其小的数,插入
if (j != i) {
arr[j] = tmp;
}
}
return arr;
}
}
如果数据排序较好时,时间复杂度就降到O(n)级别,但我们算时间复杂度都是按最差情况来看的
二分查找
public class RecursionDemo {
public static void main(String[] args) {
//二分查找 折半查找
int[] arr = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};
int index = binarySearch(arr,0, arr.length - 1, 13);
System.out.println(index);
}
//在数组arr中 L~R区间内进行二分搜索查找key的角标
private static int binarySearch(int[] arr, int L, int R, int key) {
if (L > R) { //元素key不存在
return -1;
}
int M = (L + R) / 2;
if (arr[M] == key) {
return M;
}
if (arr[M] < key) {
return binarySearch(arr,M + 1, R, key);
} else {
return binarySearch(arr,L, M - 1, key);
}
}
}
拓展
- (升序有序列表)查找大于某个数字,最左侧的数字,即大于并且最靠近
思路:
二分查到一个数字,如果比它小则截取右边,否则截取左边,最后剩下两个数字,右侧的就是找的数字
- (升序有序列表)查找局部最小值,找到一个即可
思路:
查找中间的数字M,如果M小于M-1且小于M+1,那么它就是局部最小
如果他不满足M小于M-1且小于M+1,那就截取比它小的那一端
一直二分到最后一定可以找到一个最小值
对数器
这个老师也讲了,作用就是
做一个代码,它可以随机产生一个数组长度和内容,进行我们的代码测试