spfa

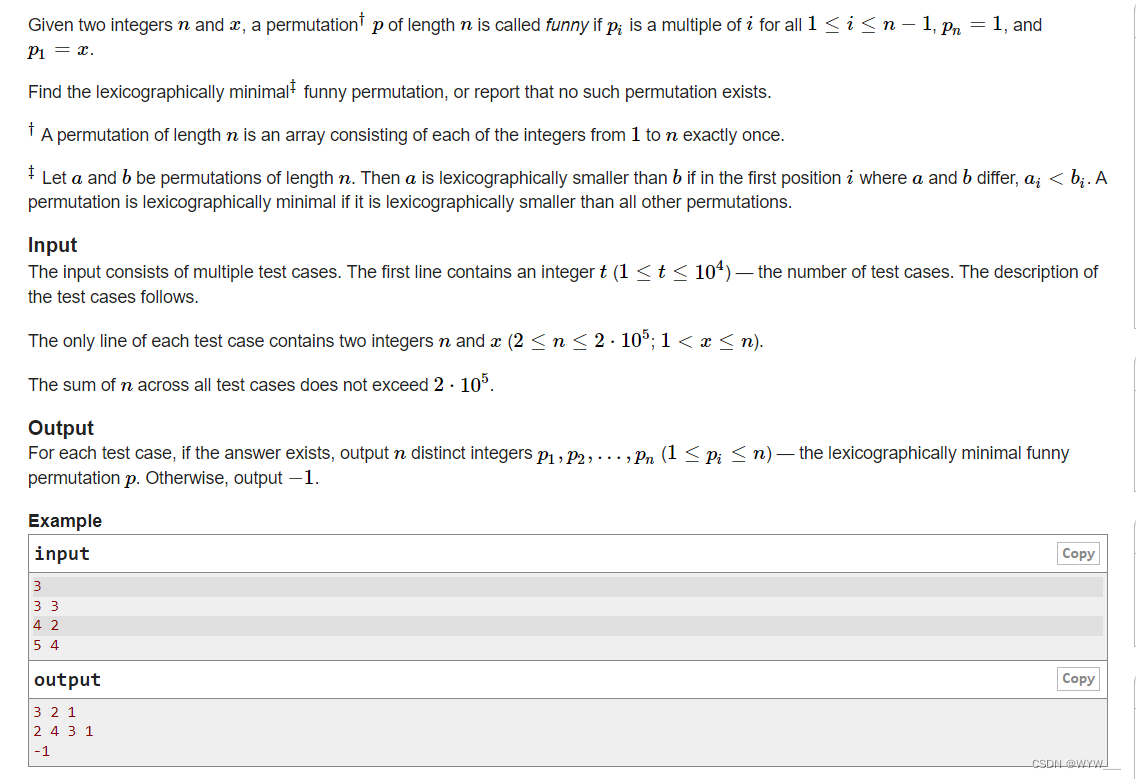
将边细分成节点，如果一条边细分出 $n$ 个结点，那么边的两个端点距离 $n+1$ ，边长 $n+1$。提示中给出，一共 $3000$ 个初始结点，无向边的数目小于等于 $10000$ ，这是提示我们最多有 $20000$ 条边。求最多可到达结点，直接求不知道走哪条边，再读读题，从一个源点出发找所有可到达的结点，转化成单源最短路问题。

这道题可以用堆优化的 $dijstra$ 或者 $spfa$ 。

$spfa$ 求出源点到所有初始结点的最短距离。维护答案变量 $ans$ ，当最大移动距离 $\ge$ 源点到结点距离，统计可到达的初始结点。再统计可到达的边上结点，从边的两个端点 $a/b$ 考虑 : 计算从源点到达 $a||b$ 点后，剩余的移动距离 $ar||br$，$a||b$ 剩余移动距离之和 $ar+br$ 就是他们可以在边上到达的结点数，如果前者大于后者，统计后者作为可到达结点数。

const int N = 3010,M = 20010;
int h[N],e[M],ne[M],w[M],idx;
int dis[N] ;//从源点到每个结点的最大距离
bool st[N] ;//当前结点是否在队列里
class Solution {
public:
    queue<int> qu;
    void add(int a,int b ,int c){
        e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
    }
    void spfa(){
        memset(dis,0x3f,sizeof(dis));
        dis[0]=0;//源点到自己距离是0
        qu.push(0);
        // st[0] = true;
        while(qu.size()){
            int t= qu.front();
            qu.pop();
            st[t] = false;
            for(int i = h[t];i!=-1;i=ne[i]){//遍历t的所有邻边
                int j = e[i];
                if(dis[j]>dis[t]+w[i]){//用t更新所有邻边的距离
                    dis[j] = dis[t] + w[i];
                    if(!st[j]) qu.push(j);//j如果不在队列,将j入队
                    st[j] = true;
                }
            }
        }

    }
    int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) {
        //edges[i][2] + 1 个结点
        //spfa求最短路(每个结点) 找最短路经过的所有结点。遍历所有边,判断最大移动和源点到两点的最短路的关系
        //判断两点剩余可移动距离相加,与两点之间边长的关系。
        memset(h,-1,sizeof h);
        for(vector<int> &edge:edges){
            int a = edge[0],b=edge[1],c=edge[2];
            add(a,b,c+1),add(b,a,c+1);
        }
        spfa();
        int ans = 0;
        for(int i = 0 ;i<n;i++)
            if(dis[i]<=maxMoves)
                ans++;
        for(auto& edge:edges){
            int a = edge[0],b= edge[1],c=edge[2];
            int ar = max(0,maxMoves-dis[a]),br = max(0,maxMoves-dis[b]);
            ans += min(ar+br,c);
        }
        idx = 0;//测试样例太多了，用了全局变量，记得idx置0
        return ans;
    }
};

时间复杂度 $O(n\times m)$ ，$n$ 是初始结点数，$m$ 是边数。 统计初始结点和$spfa$ 的平均时间复杂度 $O(n)$ ，最坏时间复杂度$O(n\times m)$。

空间复杂度 $O(N+M)$ ，结点的最大数量 $N=3000$ ，边的最大数量 $M=20000$ ，空间复杂度 $O(N+M)$ 。

致语

理解思路很重要。
欢迎读者在评论区留言，答主看到就会回复的。

AC