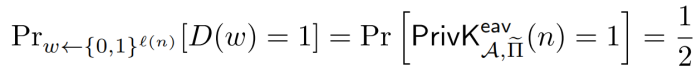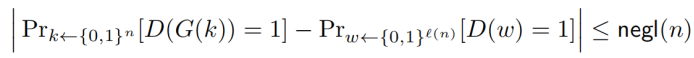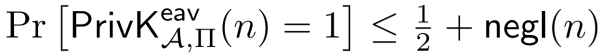目录
3.3.3 基于伪随机发生器的EAV安全
用伪随机发生器进行加密的图示
CONSTRUCTION 3.17 一种基于伪随机发生器的私钥加密方案
THEOREM 3.16 基于伪随机发生器的私钥加密方案的EAV安全
THEOREM 3.16 的证明
最后来理一下
3.3.3 基于伪随机发生器的EAV安全
用伪随机发生器进行加密的图示

CONSTRUCTION 3.17 一种基于伪随机发生器的私钥加密方案
设G是一个膨胀系数为l(n)的伪随机发生器,定义一个对于消息长度为l(n)的固定长度的私钥加密方案
Gen:在输入为1^n时,均匀选择k∈{0,1}^n作为密钥输出。
Enc:输入为k和消息m∈{0, 1}^l(n),输出密文c := G(k)⊕m
Dec:输入为k和密文c∈{0, 1}^l(n),输出明文m := G(k)⊕c
THEOREM 3.16 基于伪随机发生器的私钥加密方案的EAV安全
如果G是一个伪随机发生器,那么对于消息长度为l(n)的固定长度的私钥加密方案3.17是EAV安全的
THEOREM 3.16 的证明
设Π表示方案3.17,其满足定义3.8。关于定义3.8的内容见下文
现代密码学导论-10-EAV安全_南鸢北折的博客-CSDN博客
我们证明了对于任何PPT敌手A,有一个可忽略的函数negl,使得
通过敌手 A 构造一个区分器 D ,将 D 的区分G的输出和一个随机字符串的能力直接与 A 分辨 Π 加密明文的能力建立联系。即区分器将敌手 A 作为自己的一个子程序来完成区分实验。假设A是一个任意的PPT敌手。我们构造了一个区分器D,它以一个字符串w作为输入,它的目标是判断w究竟是真随机比特串,还是由伪随机发生器生成的伪随机比特串。我们构造D,使它模拟A的窃听实验,如下所述,并观察A是否成功。如果A成功了,那么D猜测w一定是一个伪随机字符串,而如果A不成功,那么D猜测w是一个随机字符串。详细构造:
区分器D:
D的输入是字符串w∈{0, 1}^l(n)。我们假设n可以由l(n)来确定
运行A(1^n)以获得一对消息m0、m1∈{0,1}^l(n)
随机均匀选择b∈{0,1},令c:= w⊕mb。
将c交给A,得到输出b’。如果为b’ = b,则输出1,否则输出0
定义加密方案Π’ = (Gen', Enc', Dec')
Π’实际上是引入了安全参数n的一次性密码本方案,这意味着Gen(1^n)输出长度为l(n)的随机均匀密钥k,使用k∈{0,1}^l(n)加密消息m∈{0,1}^l(n)得到c:= k⊕m。由于一次性密码本是具有完善保密性的,因此、
分析D的行为,主要的观察结果是:
如果w是真随机比特串,A作为D的子进程运行时,相当于在进行实验

因为D正好在A的窃听实验成功时输出1,即得到下面的式子,记为A式
其中第一个概率Pr的下标只是明确地表示w是均匀地从{0,1}^l(n)中选择的
如果w是由真随机k∈ {0, 1}^n生成的,我们记作w := G(k)。A作为D的子进程运行时,相当于在进行实验
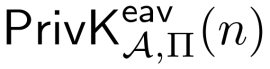
因此我们得到下面的式子,记为B式
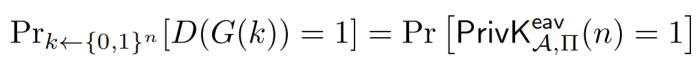
根据文章
现代密码学导论-12-伪随机发生器_南鸢北折的博客-CSDN博客
DEFINITION 3.14 伪随机发生器的定义
由于G是一个伪随机发生器,其具有伪随机性
伪随机性:对于任何ppt算法D,有一个可忽略函数negl,使得
Pr[D(G(s)) = 1] − Pr[D(r) = 1]≤ negl(n)
应用该式子于当前情况,我们得到
联立刚刚得到的A式和B式,我们得到
由于A是一个任意的PPT敌手,这就完成了Π是EAV安全的证明
最后来理一下
- 我们要证明的结论是什么??
我们要证明基于伪随机发生器G构建的方案3.17是EAV安全的,参考
现代密码学导论-10-EAV安全_南鸢北折的博客-CSDN博客
DEFINITION 3.8 EAV-安全的等价定义(一)
根据EAV安全的定义,也就是要证明对于任何PPT敌手a,存在可忽略函数negl使得
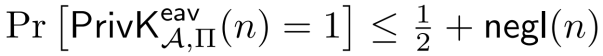
- 我们可以利用的条件是什么??
由于G是一个伪随机发生器,其具有伪随机性,参考
现代密码学导论-12-伪随机发生器_南鸢北折的博客-CSDN博客
上文中DEFINITION 3.14 伪随机发生器的定义 中的第二个条件
伪随机性:对于任何ppt算法D,有一个可忽略函数negl,使得
Pr[D(G(s)) = 1] − Pr[D(r) = 1]≤ negl(n)
我们观察一下条件和结论,条件是关于区分器算法D的,结论是关于不可区分实验的
如何把两者联系起来?我们使用归约算法,即用参与不可区分实验的敌手A来构建区分器D
我们基于为伪随机发生器定义的方案3.17为Π= (Gen, Enc, Dec),该方案使用伪随机数对明文进行加密
还定义了方案Π’= (Gen', Enc', Dec'),该方案使用真随机数对明文进行加密
根据区分器D的定义,D输出为1的概率等于敌手A在区分实验中成功的概率,
当区分器D的输入为伪随机数时,就相当于敌手A在做关于方案Π的不可区分实验,得到A式
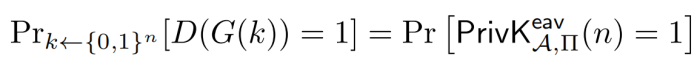
当区分器D的输入w为真随机数时,就相当于敌手A在做关于方案Π’的不可区分实验,得到B式
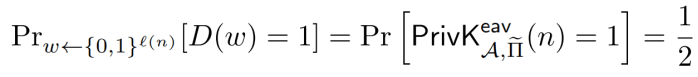
这样我们得到了两个式子,这两个式子都含有区分器D与不可取分实验的关系。这样我们就解决了之前“如何把两者联系起来”的问题。
根据G的伪随机性:Pr[D(G(s)) = 1] − Pr[D(r) = 1]≤ negl(n),即

将上式与A式和B式联立,得到
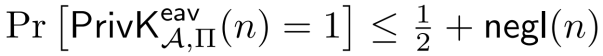
这恰好是EAV安全的定义。