文章目录
- 🚩并查集的理解
- 🚩并查集的结构与原理
- 🚩并查集的实现
- 🍁整体框架
- 🍁路径压缩
- 🚩总结
🚩并查集的理解
并查集是基于数组操作的一个特殊数据结构,和以前学习[数组的堆排序]时有点相似,只不过这次的并查集用的是双亲描述法。我们知道数组的堆排序就是为了提高排序的效率,那么并查集是为了干什么呢?这里我先不讲并查集具体的数据结构,先引入一些日常的例子来说明并查集到底是干什么的。
就以老师给学生分组为例来理解。
假如有10个学生和1个老师,现在老师刚刚认识这些学生,由于不了解每个学生的具体状态和性格,就暂时没有给学生分组。那么此时的每个学生就相当于自己单独一个集合。过了一段时间之后,老师觉得自己有所了解学生们了,于是呢就将学生给分到了不同的小组。此时学生就形成了多个集合。又过了一段时间,老师认为之前分的小组不够彻底,于是又将一些小组给合并了起来。此时又完成了不同集合的合并,形成了新的集合群。现在呢,老师只需要任命一些学生作为这些不同小组的组长(代表),任命的时候就告诉非组长的学生他们的组长是谁,那么下次老师在找两个学生时,就能通询问他们的组长,从而知道这两个学生属不属于某个共同的小组。
老师通过这种方式,就能把所有的学生发分成不同的集合来管理,完成逻辑上查询两个成员到底属于不属于同一个集合,而不用一个集合一个集合的去排查到底有没有同时拥有这两个学生。这是一种逆向管理的思维。
🚩并查集的结构与原理
上面提到,并查集就是对数组的一些操作,并且每个非集合代表的元素都知道自己的上一级所属组长是谁,那么是否可以这样思考:数组的下标与元素一一对应(映射)起来,然后数组刚开始都存-1,表示自己是一个集合的代表,并且成员个数就是 abs(-1)=1。之后只要合并某两个元素时,就将他们所在的集合A,B合并。此时假设B集合被合并到A集合中去,那么就将被集合B的根(集合代表,以下就统称根了)的数组内容改为集合A的根的下标,表示集合B的根已经不再是其成员的根了,集合A的根才是现在集合A与B的所有成员的根。所以还需要将集合A原来的元素个数加上集合B的元数个数才行。
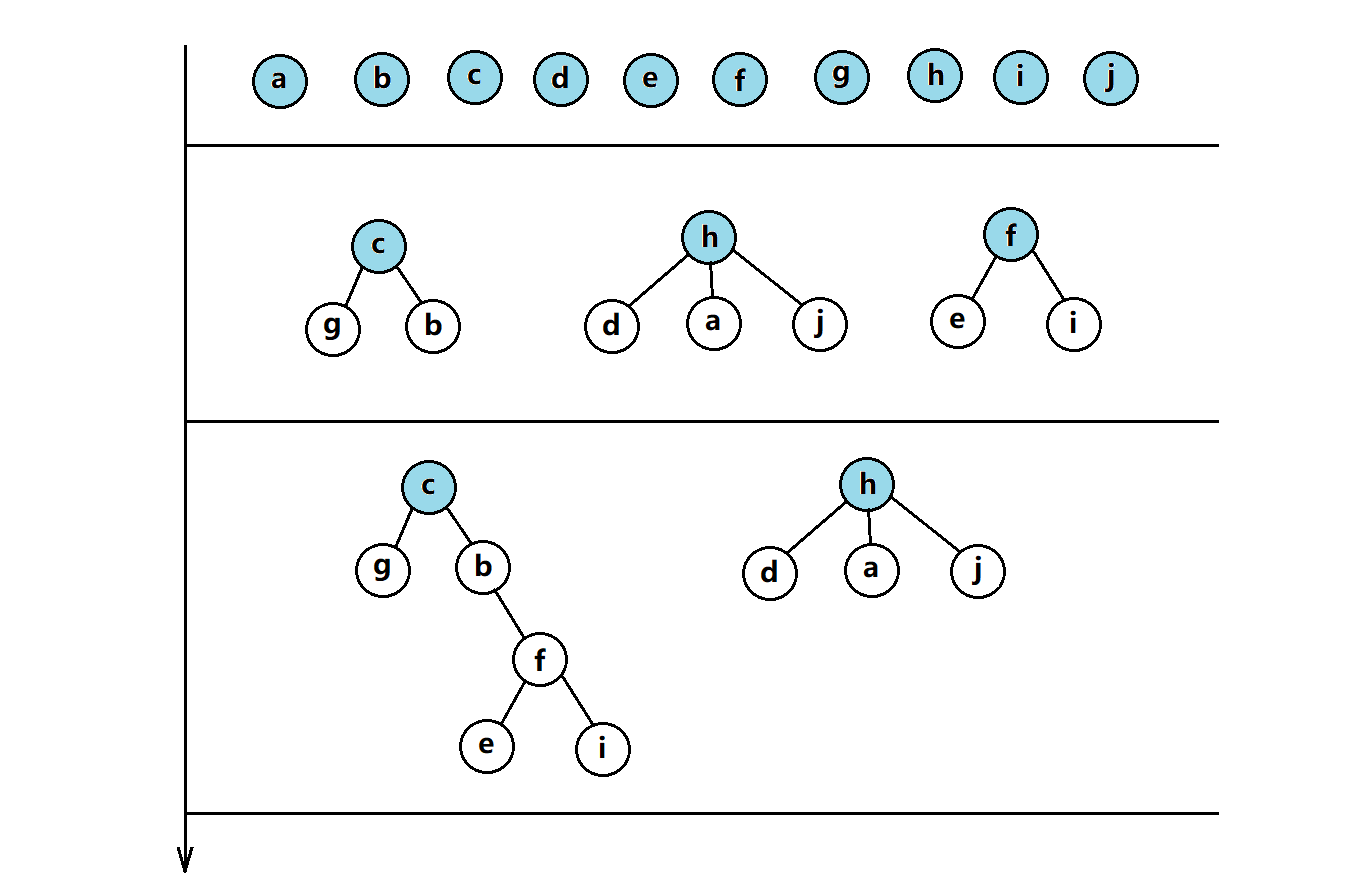
上面巴拉巴拉的说了一大通,有些同学可能没看懂,没关系,我们画个图来辅助理解。
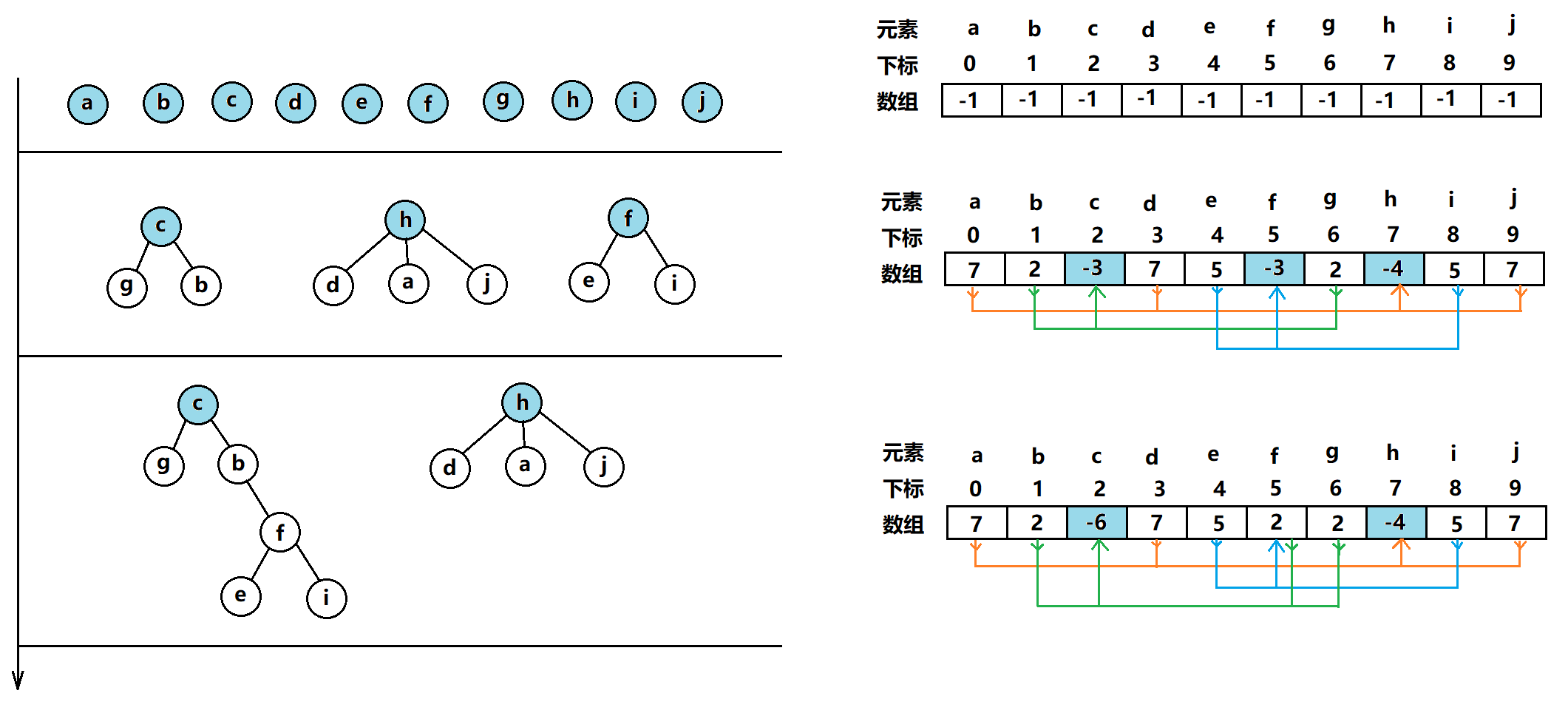
上面的图可以看出每个成员都可以顺着数组内的下标找到自己所在集合的根节点,例:e[5] -> f[2] -> c[-6],即e属于c的集合
🚩并查集的实现
下面我用的是C++实现的,但其实和C语言差不多,主要是各个函数的实现的思想最重要。模板不同是语言造成的,并不影响大家学习,这点放心哈~
🍁整体框架
#include <iostream>
#include <vector>
using namespace std;
class UnionFindSet
{
private:
vector<int> _ufs; //就相当于一个数组,用来存放每个元素上一级节点的下标
public:
UnionFindSet(size_t n)
: _ufs(n, -1) //构造函数,在创建并查集的时候直接将数组_ufs初始化n个空间,并都复制为-1
{
}
//找一个元素的根节点下标,x为元素的下标
int FindRoot(int x)
{
if (x >= _ufs.size()) //越界查寻
{
cerr << "out of range" << endl;
exit(2);
}
int root = x; //初始化根节点为x,以防查找到元素的下标就是x
while (_ufs[root] >= 0)//只要对应的数组内容>0就说明了还没找到,根节点的特征就是对应的数组内容<0
{
root = _ufs[root]; //继续向上一级查询
}
//查找的时候顺便压缩路径
//使得被查找的成员与它上面的所有非根成员直接归属在根下面
int parent;
while (_ufs[x] >= 0)
{
parent = _ufs[x];//先保存上一级的下标
_ufs[x] = root; //将此时的节点直接链在根节点下
x = parent; //x更新成保存的上一级下标,检测上一级是否直接在根节点下了
}
return root;
}
//将两个集合联合起来
void Union(int x1, int x2)
{
//找到两个元素对应的根的下标
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
//同一个集合下的话就不做处理
if (root1 == root2)
{
return;
}
//将较小的集合并在较大的集合中去,主要是尽量减少合并后找根的深度
if (abs(_ufs[root1]) < abs(_ufs[root2]))
{
swap(root1, root2);
}
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
//两个成员是否在同一个集合中
bool InSet(int x1, int x2)
{
return FindRoot(x1) == FindRoot(x2);//根对应的下标相同
}
//集合的个数,也就是数组中<0的个数
int SetSize()
{
int n = 0;
for (size_t i = 0; i < _ufs.size(); ++i)
{
if (_ufs[i] < 0)
{
++n;
}
}
return n;
}
//显示数组内的内容
void Show()
{
for (size_t i = 0; i < _ufs.size(); ++i)
{
cout << _ufs[i] << " ";
}
cout << endl;
}
};
⌨测试代码:
我就按照前面给的图进行测试了
void test_UnionFindSet()
{
//abcdefghij
UnionFindSet ufs(10);
ufs.Union(2, 6);//c<-g
ufs.Union(2, 1);//c<-b
ufs.Union(7, 3);//h<-d
ufs.Union(7, 0);//h<-a
ufs.Union(7, 9);//h<-j
ufs.Union(5, 4);//f<-e
ufs.Union(5, 8);//f<-i
ufs.Union(1, 5);//b<-f
ufs.Show();
}
int main()
{
test_UnionFindSet();
return 0;
}
💻测试结果:

与我们画的图的结果一模一样。
🍁路径压缩
实现的代码上面已经有了,我再给拿下来方便大家理解图解
//找一个元素的根节点下标,x为元素的下标(查找的过程中顺便实现路径的压缩)
int FindRoot(int x)
{
if (x >= _ufs.size()) //越界查寻
{
cerr << "out of range" << endl;
exit(2);
}
int root = x; //初始化根节点为x,以防查找到元素的下标就是x
while (_ufs[root] >= 0)//只要对应的数组内容>0就说明了还没找到,根节点的特征就是对应的数组内容<0
{
root = _ufs[root]; //继续向上一级查询
}
//查找的时候顺便压缩路径
//使得被查找的成员与它上面的所有非根成员直接归属在根下面
int parent;
while (_ufs[x] >= 0)
{
parent = _ufs[x];//先保存上一级的下标
_ufs[x] = root; //将此时的节点直接链在根节点下
x = parent; //x更新成保存的上一级下标,检测上一级是否直接在根节点下了
}
return root;
}
接下来来测试一下找根的过程的压缩处理:
void test_UnionFindSet()
{
//abcdefghij
UnionFindSet ufs(10);
ufs.Union(2, 6);//c<-g
ufs.Union(2, 1);//c<-b
ufs.Union(7, 3);//h<-d
ufs.Union(7, 0);//h<-a
ufs.Union(7, 9);//h<-j
ufs.Union(5, 4);//f<-e
ufs.Union(5, 8);//f<-i
ufs.Union(1, 5);//b<-f
ufs.Show();
ufs.Union(7,8);//将i与h联合起来
ufs.FindRoot(8);//此时再找i对应的根,看压缩处理是否正确
ufs.Show();
}
int main()
{
test_UnionFindSet();
return 0;
}
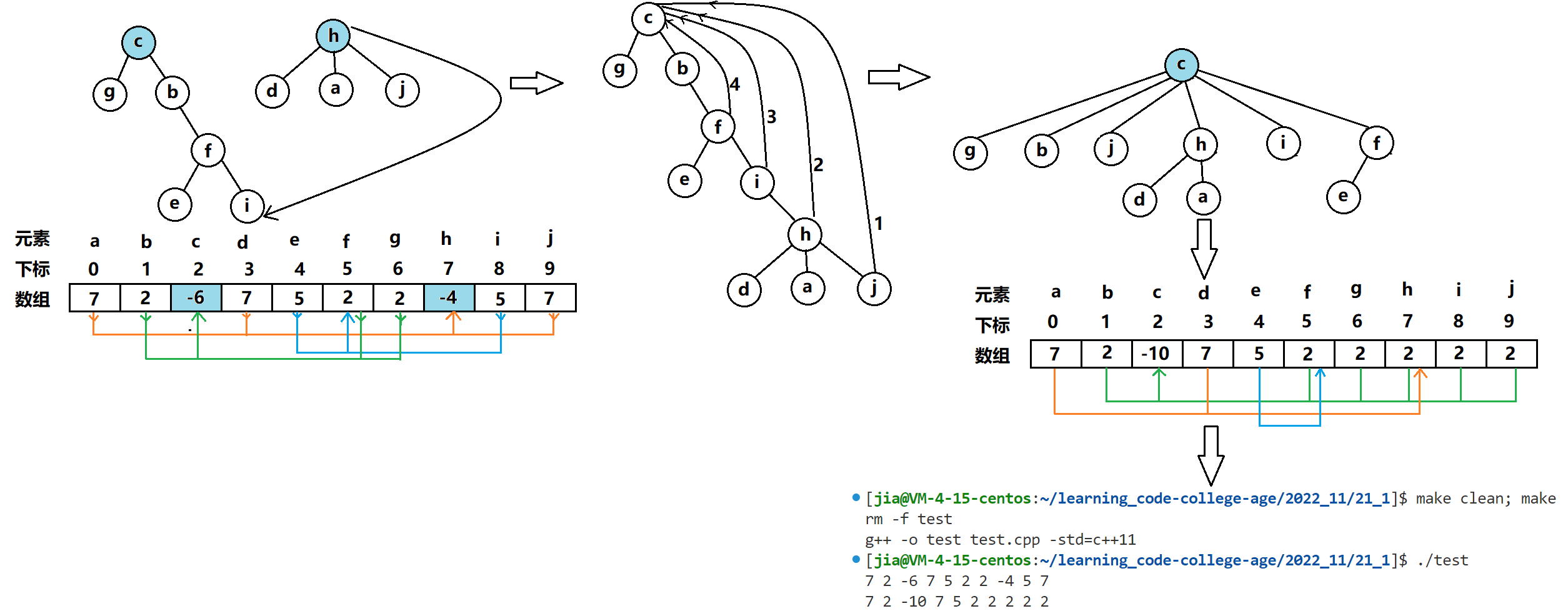
压缩路径和预期的一样,逻辑正确。
🚩总结
并查集的学习重点在于将集合处理与数组操作联系在一起,难点在于将具体的集合问题抽象成数字的处理,实在不懂的话就自己动手画一画图,结合着上面的代码和截图自己跟着一步一步调试,总会搞明白的,也不是特别难哈,加油🐾~





![[附源码]java毕业设计一点到家小区微帮服务系统](https://img-blog.csdnimg.cn/2bd921fc0b6e49fc8da576fca9f1b3a8.png)