文章目录
- 1：一元泰勒展开公式
- 2：二元泰勒展开公式
- 3：二元函数的黑塞矩阵
- 4：多元函数的黑塞矩阵
- 其他链接
1：一元泰勒展开公式
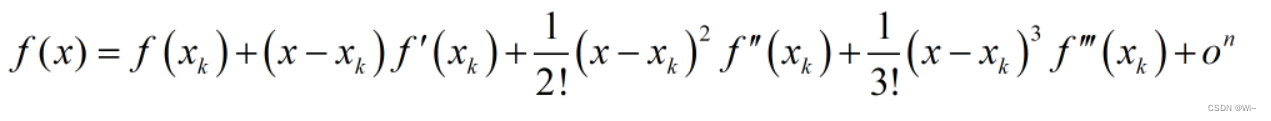举例：f(x) = 3x² + 2x + 5 在x=0或x=1处的泰勒展开
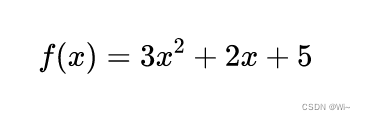
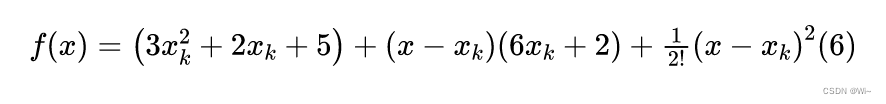当x=0时：
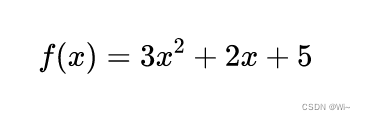
当x=1时：
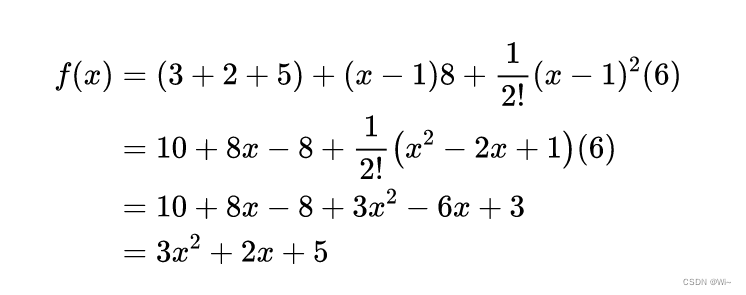
不论Xk等于多少，最后展开得公式相加都是等于f(x) = 3x² + 2x + 5
2：二元泰勒展开公式
x 和 y在k处的泰勒展开：
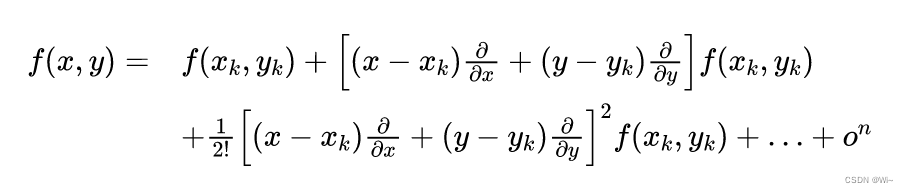
简化：
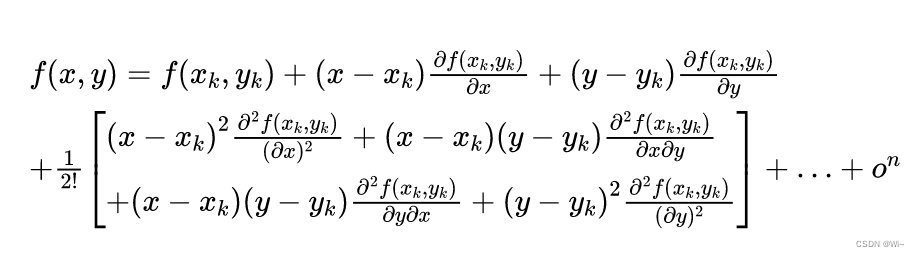
简化：
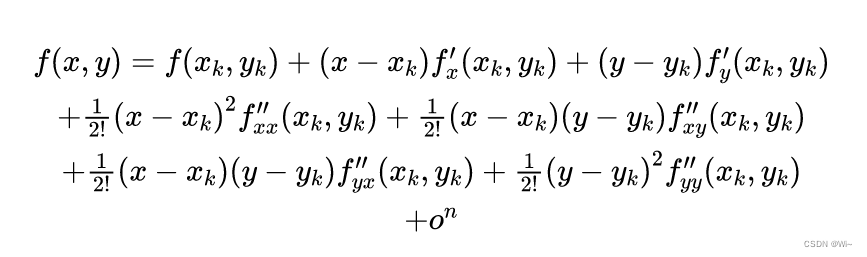①
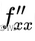是对 x 求两次导。
②
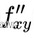
是先对x求一次导，然后再对y求一次导。
③
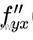
是先对y求一次导，然后再对x求一次导。
（其中③ = ②）
④
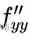是对 y 求两次导。
3：二元函数的黑塞矩阵
二元函数点
f
(
x
1
,
x
2
)
f(x_1,x_2)
f(x1,x2) 在
X
(
k
)
(
x
1
(
k
)
,
x
2
(
k
)
)
X^{(k)}(x_1^{(k)},x_2^{(k)})
X(k)(x1(k),x2(k))处的泰勒展开式为：
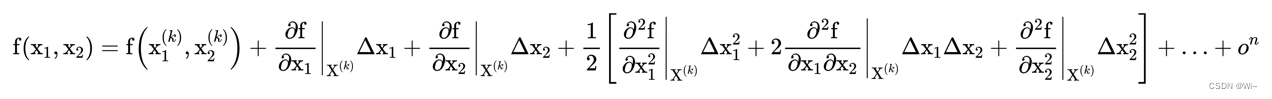
其中 Δ x 1 Δ x_1 Δx1 = x 1 x_1 x1 − x 1 ( k ) x_1^{(k)} x1(k) , Δ x 2 Δ x_2 Δx2 = x 2 x_2 x2 − x 2 ( k ) x_2^{(k)} x2(k)
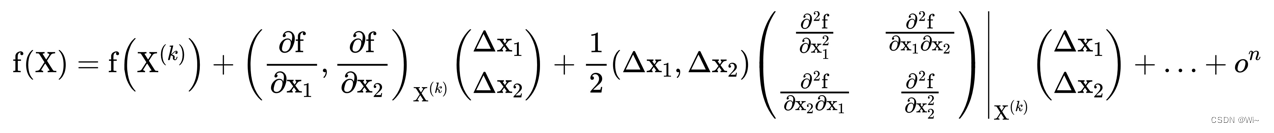
即：
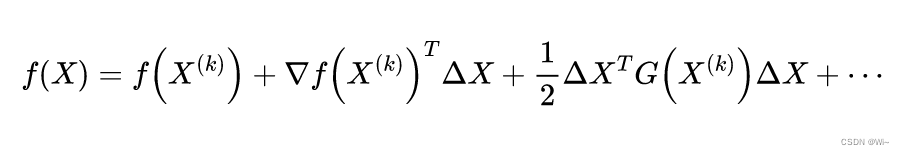
（1）：其中
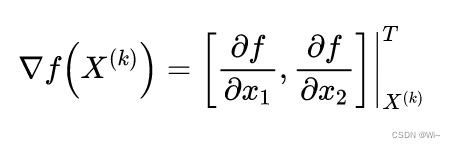
它是 f ( X ) f(X) f(X)在 X ( k ) X^{(k)} X(k)点处的梯度。
（2）：
G
(
X
(
k
)
)
G(X^{(k)})
G(X(k))是
f
(
x
1
,
x
2
)
f(x_1,x_2)
f(x1,x2)在
X
(
k
)
X^{(k)}
X(k)处的黑塞矩阵。它是由函数
f
(
x
1
,
x
2
)
f(x_1,x_2)
f(x1,x2)在
X
(
k
)
X^{(k)}
X(k)处的二阶偏导数所组成的方阵。
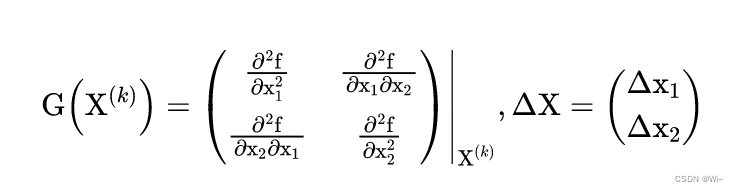
4：多元函数的黑塞矩阵
多元函数
f
(
x
1
,
x
2
,
.
.
.
,
x
n
)
f(x_1,x_2,...,x_n)
f(x1,x2,...,xn)在点
x
(
k
)
x^{(k)}
x(k)处的泰勒展开式为：
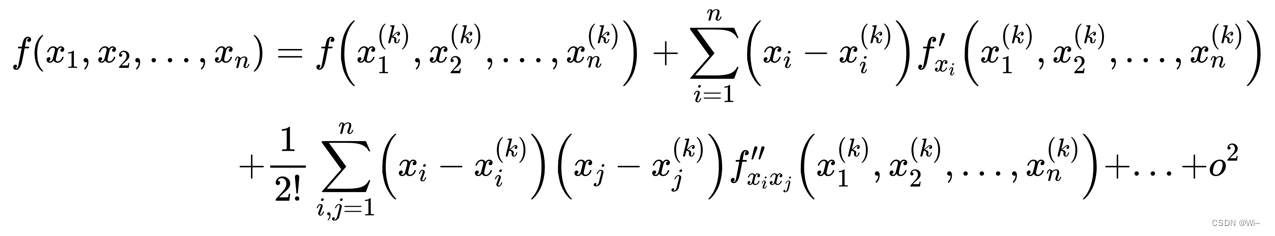把泰勒（Taylor）展开式写成矩阵的形式：
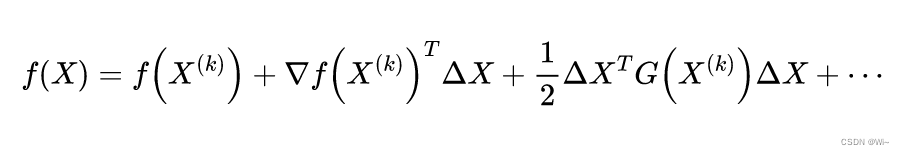其中：
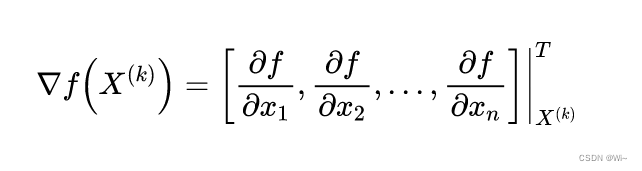
它是
f
(
X
)
f(X)
f(X)在
X
(
k
)
X^{(k)}
X(k)点处的梯度。
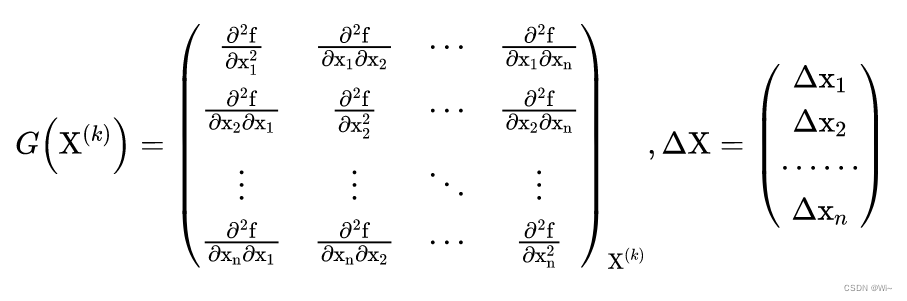
（2）：
G
(
X
(
k
)
)
G(X^{(k)})
G(X(k))是
f
(
x
1
,
x
2
,
.
.
.
,
x
n
)
f(x_1,x_2,...,x_n)
f(x1,x2,...,xn)在
X
(
k
)
X^{(k)}
X(k)处的黑塞矩阵。它是由函数
f
(
x
1
,
x
2
,
.
.
.
,
x
n
)
f(x_1,x_2,...,x_n)
f(x1,x2,...,xn)在
X
(
k
)
X^{(k)}
X(k)处的二阶偏导数所组成
n
∗
n
n*n
n∗n阶方阵。
其他链接
黑森矩阵
黑塞矩阵和雅克比矩阵
雅克比矩阵
![[附源码]java毕业设计社区志愿者服务系统](https://img-blog.csdnimg.cn/b1503ad0153941b7be4ebd4fe1292bf3.png)
![第五届“传智杯”全国大学生计算机大赛（练习赛）[传智杯 #5 练习赛] 时钟](https://img-blog.csdnimg.cn/4a765f370e834973b2c87ccf6f8d60f1.png)
