Verilog 中主要用以下 4 种系统任务来显示（打印）调试信息：$display, $write, $strobe, $monitor。

$display

$display 使用方法和 C 语言中的 printf 函数非常类似，可以直接打印字符串，也可以在字符串中指定变量的格式对相关变量进行打印。例如：

$display("This is a test.");   //直接打印字符串
$display("This is a test number: %b.", num); //打印变量 num 为二进制格式

如果没有指定变量的显示格式，变量值会根据在字符串的位置显示出来，相当于参与了字符串连接。例如：

$display("This is a test number: ", num, "!!!");

如果没有指定格式，$display 默认显示是十进制。$displayb, $displayo, $displayh 显示格式分别为二进制、八进制、十六进制。同理也有 $writeb, $writeo, $writeh, $strobeb 等。

下表是常用的格式说明。

%h 或 %H	十六进制格式输出	%c 或 %C	ASCII 码格式输出
%d 或 %D	十进制格式输出	%e 或 %E	指数格式输出
%o 或 %O	八进制格式输出	%f 或 %F	浮点数 (real 型) 格式输出
%b 或 %B	二进制格式输出	%t 或 %T	当前时间格式输出
%s 或 %S	字符串格式输出	%m 或 %M	当前层次访问路径输出

还可以使用转义字符显示特殊字符，例如：

\n	换行符	%%	百分号"%"
\t	制表符（Tab 键）	\0	八进制代表的字符
\\	反斜杠"\"符	\0x	十六进制代表的字符
\"	双引号

$write

        $wirte 使用方法与 $display 完全一样，只是前者会在每次显示信息完毕后不会自动换行，后者会自动换行。当输出后不需要换行时，可以使用显示任务 $write。

$write("This is a test");
$write("number: %b", num);
$write("!!!\n");

$strobe

        $strobe 为选通显示任务。$strobe 使用方法与 $display 一致，但打印信息的时间和 $display 有所差异。当许多语句与 $display 任务在同一时间内执行时，这些语句和 $display 的执行顺序是不确定的，一般按照程序的顺序结构执行。$strobe 则是在其他语句执行完毕之后，才执行显示任务。例如：

实例

   reg [3:0]  a ;
   initial begin
      a = 1 ;
      #1 ;
      a <= a + 1 ;
      //第一次显示
      $display("$display excuting result: %d.", a);
      $strobe("$strobe excuting result: %d.", a);
      #1 ;
      $display();
      //第二次显示
      $display("$display excuting result: %d.", a);
      $strobe("$strobe excuting result: %d.", a);
   end

        执行第一次显示任务时，非阻塞赋值与 $display 同时执行，$display 显示赋值之前的变量值，而 $strobe 显示赋值之后的变量值。这正体现了 $strobe 的选通显示特性。

 integer  i ;
   initial begin
      for (i=0; i<4; i=i+1) begin
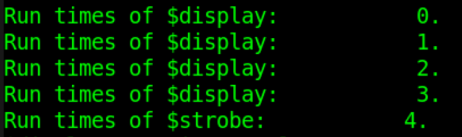
         $display("Run times of $display: %d.", i);
         $strobe("Run times of $strobe: %d.", i);
      end
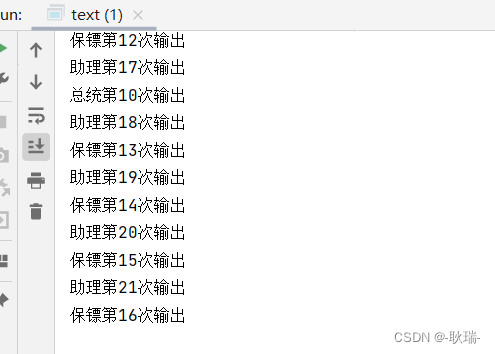
   end

执行结果如下：

        $display 按照程序结构，执行显示操作 4 次。而此循环语句是在 0 时刻执行的，所以 $strobe 显示的变量值是循环结束时变量的结果，即 i=4 退出循环后 $strobe 才会执行。这就体现了显示任务 $strobe 的时刻显示特性。

$monitor

$monitor 为监测任务，用于变量的持续监测。只要变量发生了变化，$monitor 就会打印显示出对应的信息。

例如:

实例

   reg [3:0]    cnt ;
   initial begin
      cnt = 3 ;
      forever begin
         # 5 ;
         if (cnt<7) cnt = cnt + 1 ;
      end
   end

   initial begin
      $monitor("Counter change to value %d at the time %t.", cnt, $time);
   end