84. 柱状图中最大的矩形

力扣题目链接

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

输入： heights = [2,4]
输出： 4

思路

42. 接雨水 (opens new window)是找每个柱子左右两边第一个大于该柱子高度的柱子，而本题是找每个柱子左右两边第一个小于该柱子的柱子。

为什么这么说呢，因为如下图所示，高为3的柱子可以继续往右边蔓延扩大面积，如果往左边的话则长度不够

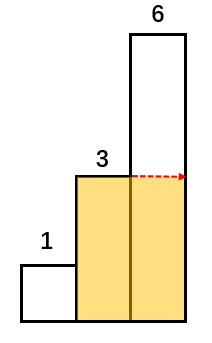
所以要找当前柱子i左右两侧第一个小于他的柱子

动态规划

对于下标i而言,能勾勒出的最大面积是什么?

以i为中心, 向左寻找第一个小于height[i]的下标minLeftIndex, 向右寻找第一个小于height[i]的下标minRightIndex, 即最大面积 = height[i] * (minRightIndex - minLeftIndex - 1)

如示例1中，求i=4的最大面积

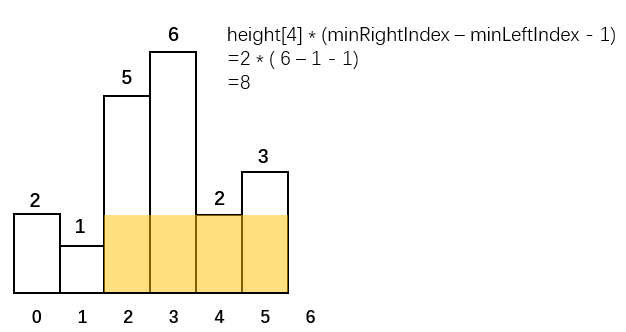
正向遍历数组 height 得到数组 minLeftIndex的每个索引值（第一小于当前柱子高度的索引值），反向遍历数组 height 得到数组minRightIndex（第一小于当前柱子高度的索引值）

完整代码：

public int largestRectangleArea(int[] heights) {
    int[] minLeftIndex = new int[heights.length];
    int[] minRightIndex = new int[heights.length];

    // 记录每个柱子 左边第一个小于该柱子的下标
    minLeftIndex[0] = -1;
    for (int i = 1; i < heights.length; i++) {
        int left = i - 1;
        // 这里不是用if，而是不断向左寻找的过程
        while (left >= 0 && heights[left] >= heights[i]) {
            left = minLeftIndex[left];
        }
        minLeftIndex[i] = left;
    }

    // 记录每个柱子 右边第一个小于该柱子的下标
    minRightIndex[heights.length - 1] = heights.length;
    for (int i = heights.length - 2; i >= 0; i--) {
        int right = i + 1;
        // 这里不是用if，而是不断向右寻找的过程
        while (right < heights.length && heights[right] >= heights[i]) {
            right = minRightIndex[right];
        }
        minRightIndex[i] = right;
    }

    // 求和
    int res = 0;
    for (int i = 0; i < heights.length; i++) {
        int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
        res = Math.max(sum, res);
    }
    return res;
}

单调栈

本题是找每个柱子左右两边第一个小于该柱子的柱子。这里就涉及到了单调栈很重要的性质，就是单调栈里的顺序，是从小到大还是从大到小。

在题解[42. 接雨水 (opens new window)]((https://blog.csdn.net/dtc1261/article/details/127930872?spm=1001.2014.3001.5502)中接雨水的单调栈从栈头（元素从栈顶弹出）到栈底的顺序应该是从小到大的顺序。

那么因为本题是要找每个柱子左右两边第一个小于该柱子的柱子，所以从栈顶到栈底的顺序应该是从大到小的顺序！

如图所示的例子

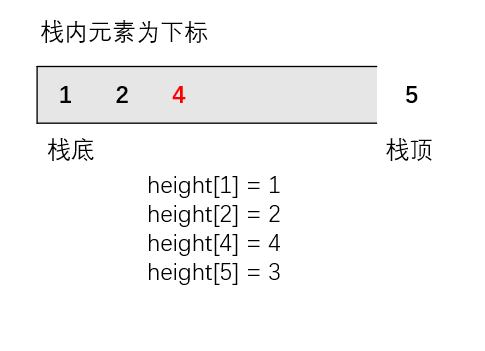
当我们遍历到height[5]时，因为栈顶到栈底是从大到小，height[5]高度是小于栈顶元素的，所以就找到了此时的栈顶元素的左右第一个小于的柱子

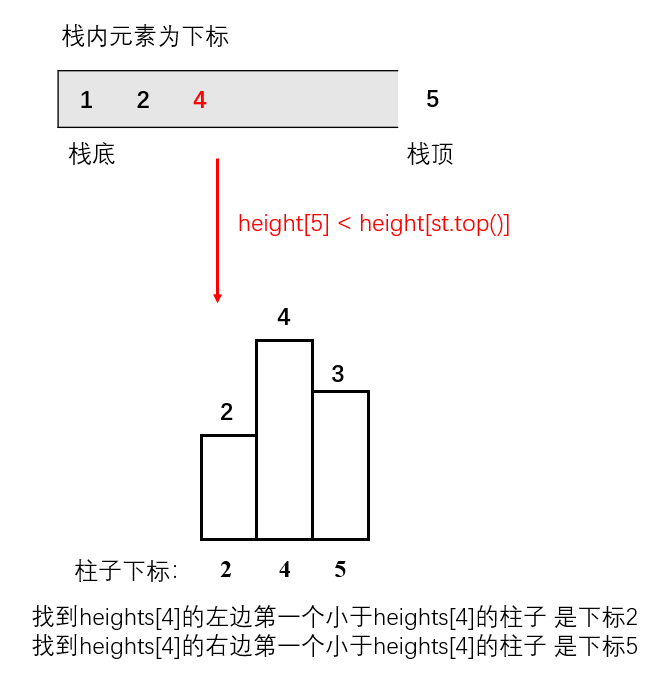
此时大家应该可以发现其实就是栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度

剩下就是分析清楚如下三种情况：

• 情况一：当前遍历的元素heights[i]小于栈顶元素heights[st.top()]的情况
• 情况二：当前遍历的元素heights[i]等于栈顶元素heights[st.top()]的情况
• 情况三：当前遍历的元素heights[i]大于栈顶元素heights[st.top()]的情况

完整代码：

public int largestRectangleArea(int[] heights) {
    Deque<Integer> stack = new LinkedList<>();
    // 数组扩容，在头和尾各加入一个元素
    int [] newHeights = new int[heights.length + 2];
    newHeights[0] = 0;
    newHeights[newHeights.length - 1] = 0;
    for (int index = 0; index < heights.length; index++){
        newHeights[index + 1] = heights[index];
    }

    // 之后就用newHeights计算
    stack.push(0);
    int res = 0;
    // 第一个元素已经入栈，从下标1开始
    for (int i = 1; i < newHeights.length; i++) {
        if (newHeights[i] > newHeights[stack.peek()]) {
            stack.push(i);
        }else if (newHeights[i] == newHeights[stack.peek()]) {
            stack.pop();
            stack.push(i);
        }else {
            // 我们要找到一个不小于newHeights[i]为止
            while (newHeights[i] < newHeights[stack.peek()]) {
                int mid = stack.peek(); // 中间柱子
                stack.pop();
                int left = stack.peek();
                int right = i;
                int w = right - left - 1;
                int h = newHeights[mid];
                res = Math.max(res, w * h);
            }
            stack.push(i);
        }
    }

    return res;
}