数据结构系列学习（九） - 循环队列（Circular_Queue）

news2025/7/11 18:36:22

目录

引言：

学习：

循环队列设计背景：

利用顺序表的思维对队列进行探讨：

解决方案的思考：

循环队列中循环的体现：

循环队列的要点：

第一个难点：

第二个难点：

第三个难点：

代码实现：

头文件（Circular_Queue.h）：

定义循环队列的初始大小：

循环队列中的元素范型定义：

循环队列的结构体设计：

所有功能函数的声明：

源文件(Circular_Queue.cpp)中对函数功能的具体实现：

初始化函数：

入队列函数：

出队列函数：

获取队头元素值函数：

搜索函数：

判空函数：

判满函数：

获取有效值个数函数：

清空函数：

销毁函数：

打印函数：

测试：

测试初始化函数、打印函数：

测试入队列函数： 

测试出队列函数： 

测试获取队头元素值函数：

测试获取队列有效长度函数： 

测试清空函数： 

​编辑

测试销毁函数：

总结：

参考资料：

引言：

数据结构系列学习（一） - An Introduction to Data Structure

数据结构系列学习（二） - 顺序表（Contiguous_List） 

数据结构系列学习（三） - 单链表(Linked_List) 

数据结构系列学习（四） - 单向循环链表(Circular Linked List) 

数据结构系列学习（五） - 双向链表（Double_Linked_List） 

数据结构系列学习（六） - 顺序栈（Stack） 

数据结构系列学习（七） - 链栈（Chain_Stack）

数据结构系列学习（八） - 链式队列（Chain_Queue） 

在上篇文章中我们了解学习了链式队列，并用代码进行了实现，在这篇文章中我们将对队列的另外表现形式——循环队列进行了解和学习，并使用代码对它进行实现。

学习：

在上篇文章中我们已经介绍了队列的相关知识及概念。

循环队列是一种抽象数据类型，也是一种数据存储的方式

循环队列设计背景：

利用顺序表的思维对队列进行探讨：

我们知道，队列这种数据类型就是一端插入，一端删除，如果我们使用顺序表去实现队列的话，则有两种可能性：

1：如果我们将顺序表的表头作为队列的出口，顺序表的表尾作为队列的入口，那么出队列和入队列的时间复杂度分别为：

此时入队列就相当于是顺序表中的尾插，并不会有元素迁移位置情况的存在，则入队列的时间复杂度为： O（1）        

此时出队列就相当于是顺序表中的头删，每删除一个元素，被删除元素后面的元素都需要统一向前挪动一位，所以出队列的时间复杂度为：O（n）

2：如果我们讲顺序表的表头作为队列的入口，顺序表的表尾作为队列的出口，那么出队列和入队列的时间复杂度分别为：

此时入队列就相当于是顺序表中的头插，如果我们要插入一个元素，就要将所有的元素均向后迁移一位为新插入的元素腾出来地方，所以入队列的时间复杂度为O（n）        

此时出队列就相当于是顺序表中的尾删，尾删函数不会牵扯到元素的迁移问题，则出队列的时间复杂度为O（1）

根据上述情况我们发现，如果我们用顺序表来队队列进行实现，是没有办法让入队列和出队列的时间复杂度都达到O（1），则我们需要对顺序队列进行修改。

解决方案的思考：

老师曾经给我们举过这样一个例子，我觉得非常恰当。我们应该都坐过绿皮火车，或者高铁，在列车中，中途你想吃泡面了，这时候你应该很少去找买泡面的人，一般都是一个人推着装着各种各样的商品的小车从第一节车厢走到最后一节车厢的。乘客本身是不动的，移动的是推着小车的乘务人员。

我们将这种思想应用到顺序表实现的队列中去，也就是我们在进行数据的插入或者删除的时候，我们不让数据去移动，而是设定两个指针，分别为队头指针和队尾指针，让这两个指针去挪动即可。

如果只是牵扯到指针的移动，那么入队列和出队列的时间复杂度就能同时降为O(1) 。

循环队列中循环的体现：

那么为什么叫它循环队列？循环又体现在哪呢？

这里我们先来画一个图：

假设我们现在在队去申请了6个整形空间内存，并且将123456这六个数进入了队列，如果我们现在需要将元素1进行出队列操作，出队列之后如图：

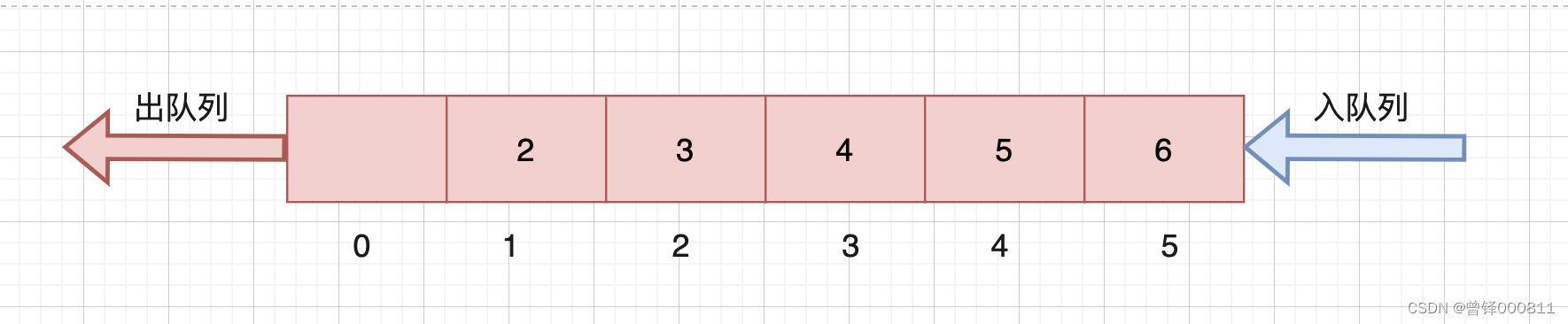
此时原先的存放元素1的内存空间现在没有存放任何数据，也就是空了，这时就相当于我们原先为6个元素申请的内存空间经过一次出队列操作之后，有一个元素的空间被浪费掉了，那么如果我们此时又需要再重新将元素1入队列， 按照队列的传统思维，这时内存空间已经不足够了，我们需要重新申请内存空间将要入队列的元素放进去。如果我们不申请，想象一下，我们如何利用刚刚浪费掉的那个空间？如图：

 

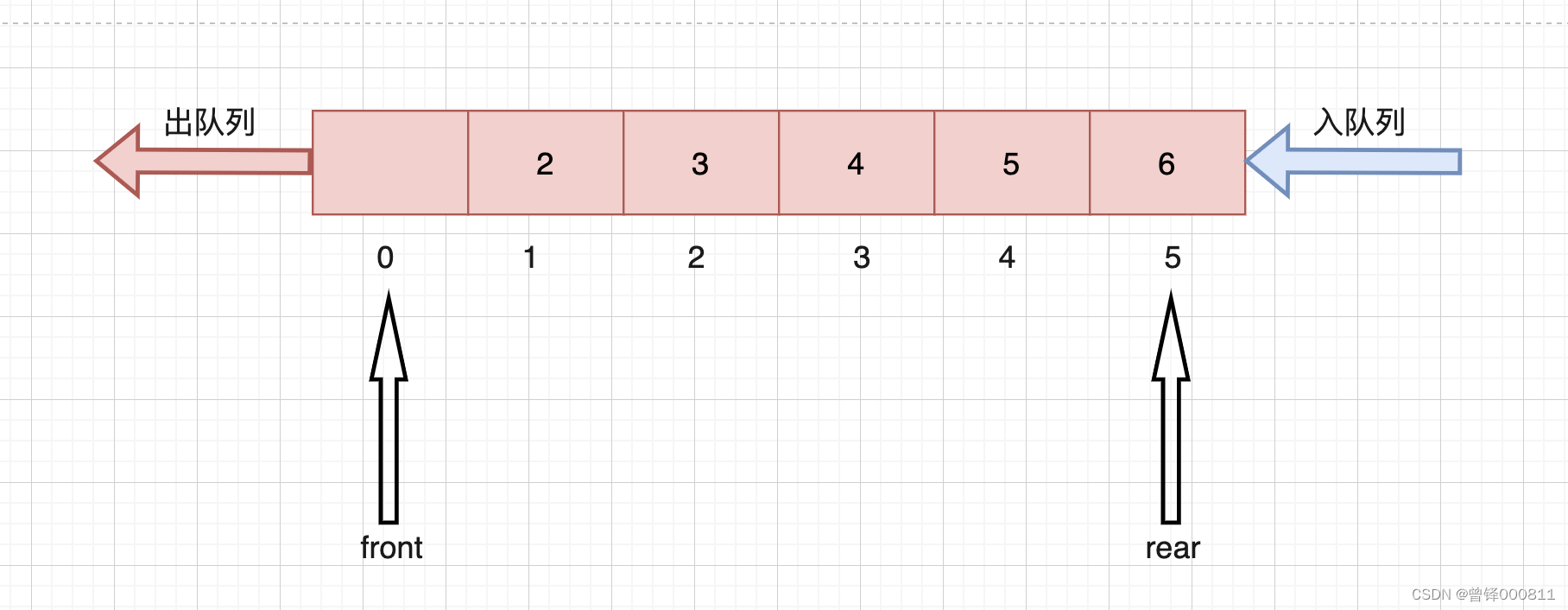
如图，我们定义两个指针front和rear， 分别指向队列的出口和入口，此时如果我们想利用已经浪费掉的空间，只需要将rear指针迁移至刚才出队列的地方即可，如图：

我们将这一结构想象成一个环状的结构，如图：

 

所以这是为了将头部出队列之后的空间也利用上，生成一个环形的结构。

也就是说，我们将数组的最后一个位置和第一个位置看作是相邻的，这样处理过后，如果数组前面有任何空闲的位置，我们只需要将rear指针移动到空闲位置即可，这样我们就能将前面的空闲的位置利用上，故环形设计可以非常有效将之前那些空间都利用上，大大提高空间的利用率。

循环队列的要点：

如果想学好循环队列，很简单，只需要记住它的三个要点：

第一个难点：

如何保证顺序表实现的队列入队和出对的时间复杂度为O（1）；

解决方案：让数据不动，让队头指针和队尾指针移动，然后又为了利用到之前队列前面已经出列的空余空间，则让队头和队尾链接成了一整体，则这种头尾相连的顺序存储结构被称为循环队列。

注意：内存中存储的还是左边这个样子，右边这个圆之时尾了方便我们去想象

第二个难点：

因为第一个难点，我们让头和尾进行相连，且数据不动指针动，则会导致出现一个问题：判空条件和判满条件冲突了。

判空条件：front == rear

判满条件：front == rear

解决方案：

第一种：加标记，结构体设计的时候，额外加一个成员，加一个有效长度length

使用第一种方案：

则判空条件为：（front == rear && length == 0）

则判满条件为：（front ==rear && length != 0）

第二种：在队尾处浪费掉一个空间不用，作为标记去使用(数据结构书里面采用的方式)。

使用第二种方案（数据结构书中采用的方法）：

则判空条件为：（front == rear）

则判满条件为：队尾指针，向后再走一步，就遇到了队头，则认为满了。

第三个难点：

因为我们将顺序表实现的队列臆想成环形，头尾相连，这样怎么求循环队列中有多少个元素？（简而言之，我们应该如何实现获取有效长度函数（Get_Length）？）

解决方案：

想方设法得到一个总的公式：

第一种：rear > front

                length == rear - front

第二种：rear < front

                length == rear - front _ MAX_SIZE

总的公式：length = (rear - front + MAX_SIZE) % MAX_SIZE

那么我们怎么记这个公式呢？

+MAX_SIZE：防止rear - front 出现负数

%MAX_SIZE：防止rear - front没有出现负数，导致+MAX_SIZE加多了 

代码实现：

我们要在循环队列中实现的功能函数：

初始化函数(Init_Queue)；

入循环队列函数(Push)；

出循环队列函数(Pop)；

获取队头元素值(Front)；

搜索函数(Search)；

判空函数(Is_Empty)；

判满函数(Is_Full)；

获取有效值个数函数(Get_Length)；

清空函数(Clear)；

销毁函数(Destroy)；

打印函数（Show）；

头文件（Circular_Queue.h）：

定义循环队列的初始大小：

#define MAX_SIZE 100

循环队列中的元素范型定义：

typedef int Elem_type;

循环队列的结构体设计：

循环队列中，我们先定义一个范指针类型的base用来接收在堆区申请的内存空间基址，这里的队头指针front和队尾指针rear我们用组的下标来进行定义，定义的长度length用来起到标记的作用。

typedef struct Queue
{
    Elem_type* base;//用来接收malloc动态内存申请的空间基址，用于分配空间
    int front;//队头指针，若队列不空，则指向队头元素
    int rear;//队尾指针，若队列不空，则指向队尾元素的下一个位置
    //int length;//用于第二个难点的解决方案，做一个标记
}Queue,*PQueue;

所有功能函数的声明：

//初始化
void Init_Queue(PQueue Circular_Queue);
//入对
bool Push(PQueue Circular_Queue,Elem_type val);
//出对
bool Pop(PQueue Circular_Queue);
//获取队头元素值
Elem_type Front(PQueue Circular_Queue);
//搜索
int Search(PQueue Circular_Queue,Elem_type val);
//判空
bool IsEmpty(PQueue Circular_Queue);
//判满
bool IsFull(PQueue Circular_Queue);
//获取有效值的个数
int Get_Length(PQueue Circular_Queue);
//清空
void Clear(PQueue Circular_Queue);
//销毁
void Destroy(PQueue Circular_Queue);
//打印
void Show(PQueue Circular_Queue);

源文件(Circular_Queue.cpp)中对函数功能的具体实现：

初始化函数：

与顺序表的初始化函数类似，因为循环队列是不存在扩容操作的，所以我们先通过malloc函数进行在堆区申请循环队列固定内存的操作，并使用base来保存这段内存的地址，然后将循环队列中的头和尾分别赋值为0即可。

//初始化
void Init_Queue(PQueue Circular_Queue)
{
    assert(Circular_Queue != nullptr);
    //在堆区申请MAX_SIZE个范型大小的空间，强转为范型指针类型，并通过循环队列的base返回出来
    Circular_Queue->base = (Elem_type*)malloc(MAX_SIZE * sizeof(Elem_type));
    assert(Circular_Queue->base != nullptr);
    //初始将循环队列中的头和尾均赋值尾0；
    Circular_Queue->front = 0;
    Circular_Queue->rear = 0;
}

入队列函数：

首先对队列进行判满操作，如果循环队列已满则直接返回为假，如果没满，将我们要插入的值赋值到base组的rear号下表位置，也就是尾部。这里需要注意，如果是普通的顺序表，那么当我们在赋值结束之后，则直接可以使用++操作直接将边界向后迁移一位，但是在循环队列中，这样的写法是错误的。我们此时将rear进行更新， 对rear进行加一操作并将两者之和对原先设定好的MAX_SIZE进行取余。

bool Push(PQueue Circular_Queue,Elem_type val)
{
    assert(Circular_Queue != nullptr);
    if(IsFull(Circular_Queue)){
        return false;
    }
    Circular_Queue->base[Circular_Queue->rear] = val;
    //队尾指针不要忘记向后走一位，但是不要用++
    //错误写法：Circular_Queue->rear++;
    Circular_Queue->rear = (Circular_Queue->rear + 1) % MAX_SIZE;
    return true;
}

出队列函数：

首先对队列进行判空操作，如果队列为空则直接返回为假，和上面一样，我们对队头的front加一并对MAX_SIZE进行取余操作。

//出队列函数
bool Pop(PQueue Circular_Queue)
{
    assert(Circular_Queue != nullptr);
    if(IsEmpty(Circular_Queue)){
        return false;
    }
    //错误写法：Circular_Queue->front++;
    Circular_Queue->front = (Circular_Queue->front + 1) % MAX_SIZE;
    return true;
}

获取队头元素值函数：

首先对队列进行判空操作，如果队列为空返回error，异常退出程序。如果队列不为空，则返回base组的front下标位置。

//获取队头元素值
Elem_type Front(PQueue Circular_Queue)
{
    assert(Circular_Queue != nullptr);
    if(IsEmpty(Circular_Queue)){
        printf("error\n");
        exit(1);
    }
    return Circular_Queue->base[Circular_Queue->front];
}

搜索函数：

与顺序查找类似，定义for循环对base组进行遍历，如果在base组中找到了和我们要找的元素相吻合的元素，则返回这个元素的下标，如果没有找到，我们就返回-1值。

//搜索函数
int Search(PQueue Circular_Queue,Elem_type val)
{
    assert(Circular_Queue != nullptr);
    for(int i = Circular_Queue->front;i != Circular_Queue->rear;i = (i + 1) % MAX_SIZE){
        if(val == Circular_Queue->base[i]){
            return i;//找到的话返回这个值的下标
        }
    }
    return -1;
}

判空函数：

当队头等于队尾的时候，队列自然也就为空了。

//判空
bool IsEmpty(PQueue Circular_Queue)
{
    assert(Circular_Queue != nullptr);
    return Circular_Queue->front == Circular_Queue->rear;
}

判满函数：

因为我们采用的是第二种方案，也就是不采用标记，直接将队列最后一个空间浪费掉，我们试着向后走一步，如果向后走一步恰好使front与rear重合，则证明队列已满。

//判满函数
bool IsFull(PQueue Circular_Queue)
{
    assert(Circular_Queue != nullptr);
    return(Circular_Queue->rear + 1) % MAX_SIZE == Circular_Queue->front;
}

获取有效值个数函数：

方法一： 

定义count整形值用来记录队列中的有效值个数，定义循环，循环条件为i不为rear，i下标每向前走一步count就加1，最后将count的值返回出来即可。这样做符合我们之前实现过的任何一种抽象数据类型的逻辑，但是如果我们使用循环那么时间复杂度就为O(n)，时间复杂度偏大，如果我们仅仅是获取有效值，还记得我们在上面总结出来的公式吗？我们可以通过公式有效地降低时间复杂度，见方法二。

//获取有效值的个数函数
int Get_Length(PQueue Circular_Queue)
{
//    方法一：直接使用循环对队列进行遍历，但是时间复杂度过高，为O(n)
    assert(Circular_Queue != nullptr);
    int count = 0;
    for(int i = Circular_Queue->front;i != Circular_Queue->rear;i = (i + 1) % MAX_SIZE){
        count++;
    }
    return count;

}

直接采用上文中提到的公式，时间复杂度就可以直接降低到O(1)：

//    方法二：利用难点三里面的方法，直接利用公式来求。
    return (Circular_Queue->rear - Circular_Queue->front + MAX_SIZE) % MAX_SIZE;

清空函数：

将循环队列中的front下标和rear下标直接赋值为0即可。

//清空函数
void Clear(PQueue Circular_Queue)
{
    assert(Circular_Queue != nullptr);
    Circular_Queue->rear = Circular_Queue->front = 0;
}

销毁函数：

直接将我们原先通过malloc函数在堆区申请的内存释放掉即可。

//销毁函数
void Destroy(PQueue Circular_Queue)
{
    assert(Circular_Queue != nullptr);
    free(Circular_Queue->base);
}

打印函数：

定义循环，对循环队列进行完整地遍历，i下标每指向一个节点就将这个节点的数据打印出来。

//打印函数
void Show(PQueue Circular_Queue)
{
    assert(Circular_Queue != nullptr);
    for(int i = Circular_Queue->front;i != Circular_Queue->rear;i = (i + 1) % MAX_SIZE){
        printf("%3d",Circular_Queue->base[i]);
    }
}

测试：

测试初始化函数、打印函数：

//循环队列测试用例
#include "Circular_Queue.h"
#include<cassert>
#include<cstdio>
#include<cstdlib>
int main()
{
    //初始化
    Queue head;
    Init_Queue(&head);
    for(int i = 0;i < 10;i++){
        Push(&head,i + 1);
    }
    printf("原始数据为：\n");
    Show(&head);
    printf("\nfront = %d , read = %d\n",head.front,head.rear);
/*
    此处添加其他测试用例......
*/
    return 0;
}

运行结果：

测试入队列函数： 

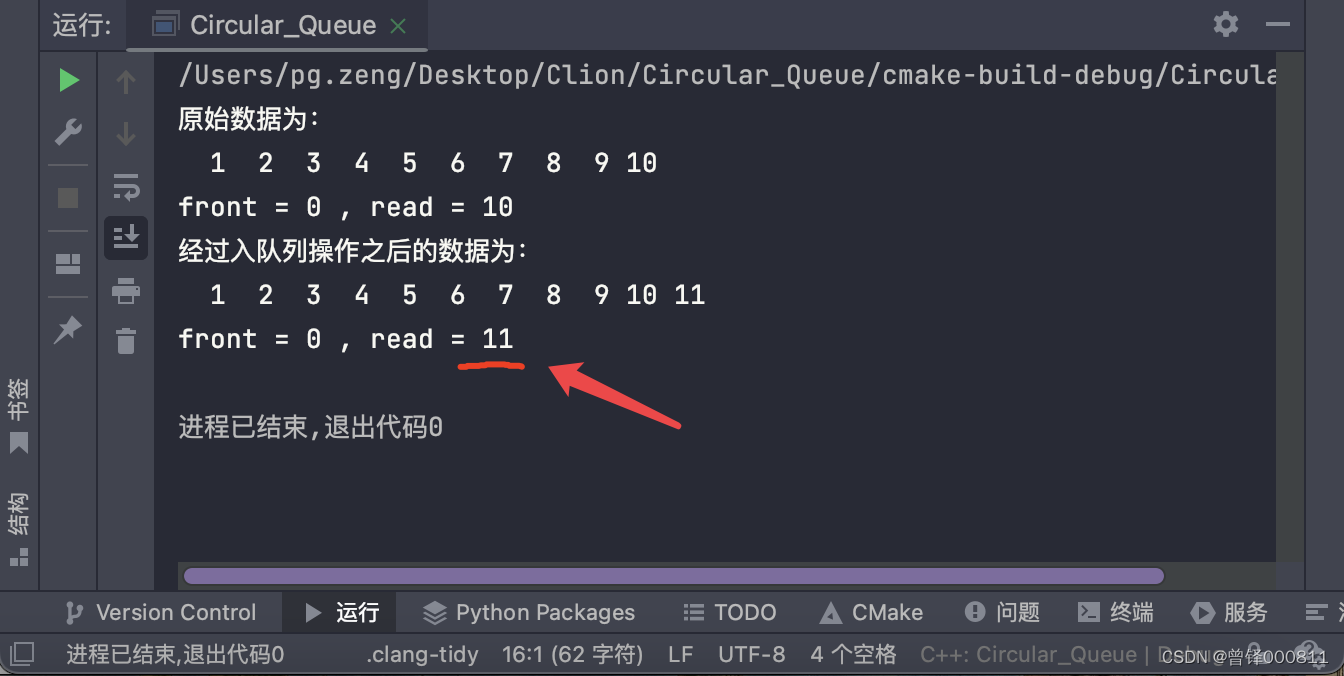
将11入队，并将入队之后的所有队列数据打印出来：

    Push(&head,11);
    printf("经过入队列操作之后的数据为：\n");
    Show(&head);
    printf("\nfront = %d , read = %d\n",head.front,head.rear);

运行结果：

 

测试出队列函数： 

进行出队列操作，并将出队列操作之后的数据全部打印出来：

    Pop(&head);
    printf("经过出队列操作之后的数据为：\n");
    Show(&head);
    printf("\nfront = %d , read = %d\n",head.front,head.rear);

运行结果：

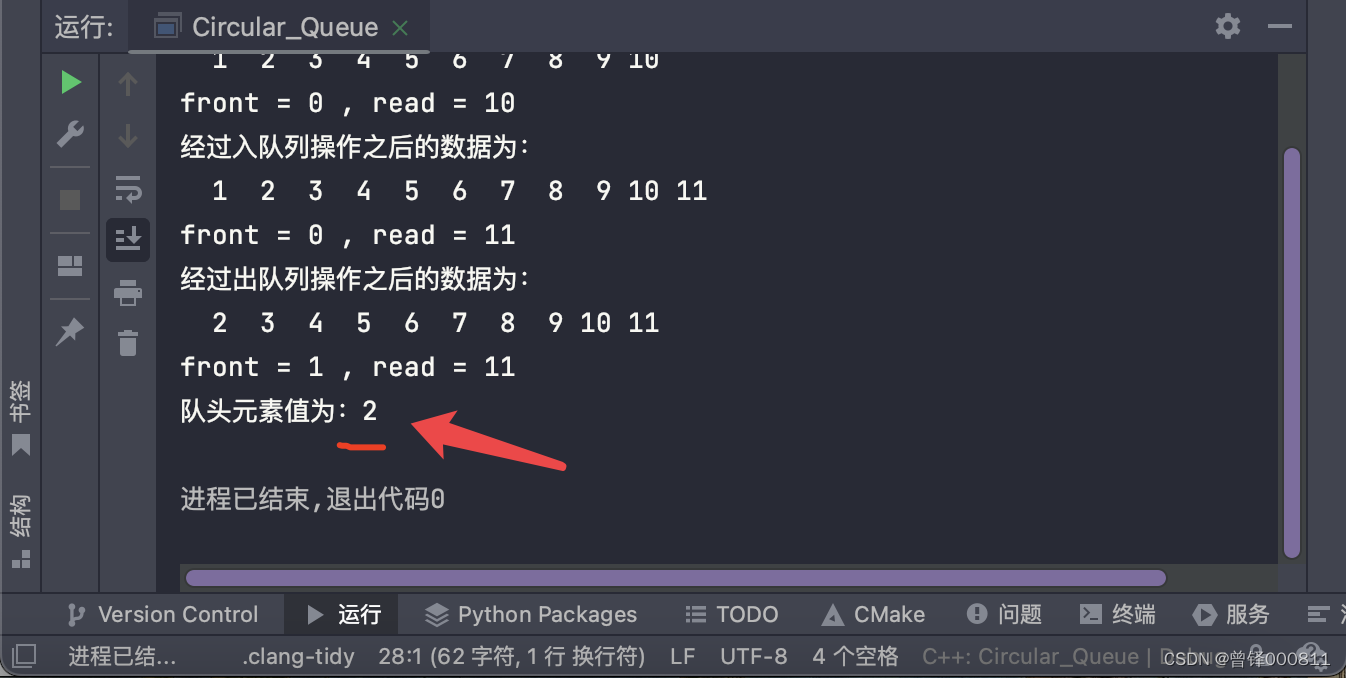
测试获取队头元素值函数：

    int front = Front(&head);
    printf("队头元素值为：%d\n",front);

运行结果：

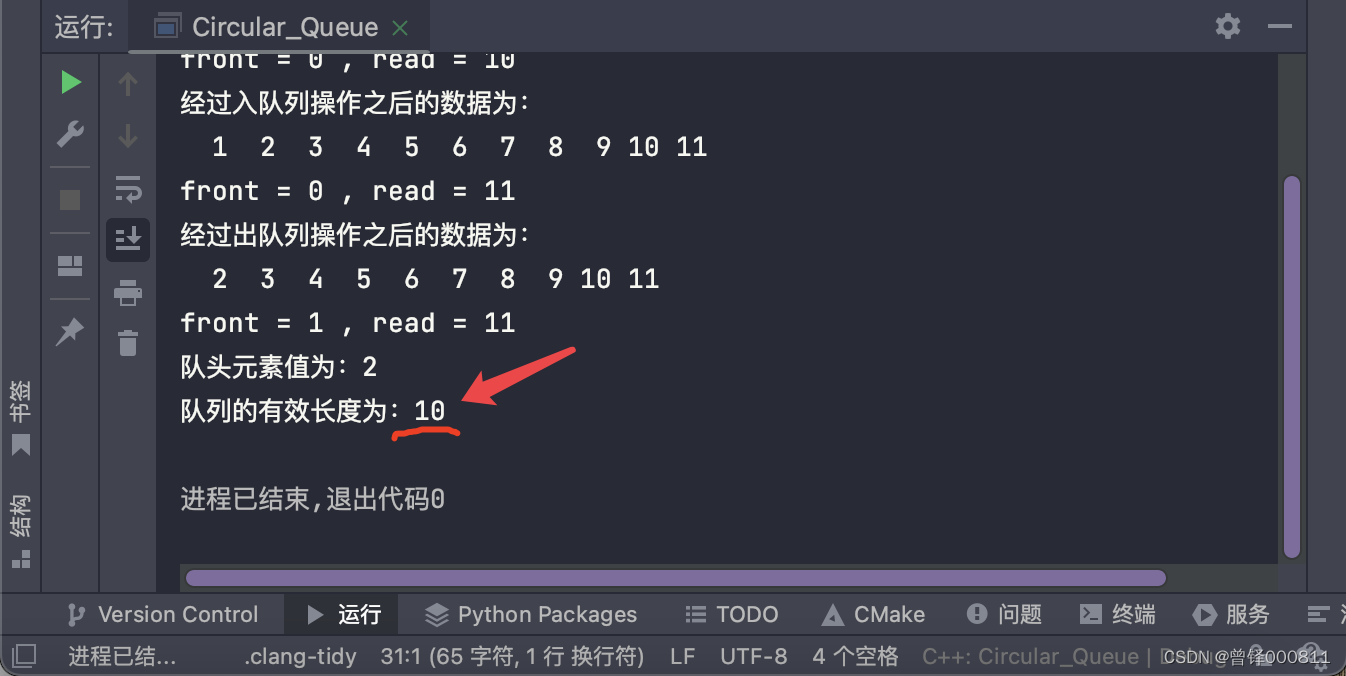
测试获取队列有效长度函数： 

定义整形值len用来保存Get_Length函数的返回值，将len打印出来。

    int len = Get_Length(&head);
    printf("队列的有效长度为：%d\n",len);

运行结果：

测试清空函数： 

    Clear(&head);
    printf("经过清空操作之后的队列为：\n");
    Show(&head);

运行结果：

测试销毁函数：

    Destroy(&head);
    printf("经过销毁操作之后的队列为：\n");
    Show(&head);

运行结果：

如图，所有在源文件中实现的函数均已测试成功。

总结：

循环队列是一种经典的抽象数据类型，实现循环队列之前我们首先要清楚循环队列和普通队列之间的区别以及循环队列的原理，循环队列相较于普通的队列能较大的提高空间的利用率，但是循环队列也有一个非常明显的缺点，就是循环队列是无法扩容的，所以当我们要使用循环队列的时候必须要对数据量有一个较为精准的估算，这样才能发挥出循环队列的优势所在。

参考资料：

那拉辛哈·卡鲁曼希 - 《数据结构与算法经典问题解析》

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/18102.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Verilog 显示任务（$display, $write, $strobe, $monitor）

Verilog 显示任务（$display, $write, $strobe, $monitor）

Verilog 中主要用以下 4 种系统任务来显示&#xff08;打印&#xff09;调试信息&#xff1a;$display, $write, $strobe, $monitor。 $display $display 使用方法和 C 语言中的 printf 函数非常类似&#xff0c;可以直接打印字符串&#xff0c;也可以在字符串中指定变量的格…
阅读更多...
7. 微服务之Docker自动化部署

7. 微服务之Docker自动化部署

7.1 Docker 介绍 Docker 是一个快速交付应用、运行应用的技术&#xff1a; 可以将程序及其依赖、运行环境一起打包为一个镜像&#xff0c;可以迁移到任意Linux操作系统运行时利用沙箱机制形成隔离容器&#xff0c;各个应用互不干扰启动、移除都可以通过一行命令完成&#xff…
阅读更多...
华清远见：驱动点灯第N回目

华清远见：驱动点灯第N回目

1.在串口工具进行输入&#xff1a; echo 1 > /dev/myled0 ---->led1灯点亮 echo 0 > /dev/myled0 ---->led1灯熄灭 echo 1 > /dev/myled1 ---->led1灯点亮 echo 0 > /dev/myled1 ---->led1灯熄灭 echo 1 > /dev/myled2 ---->led1灯点亮 ec…
阅读更多...
力扣刷题day52|84. 柱状图中最大的矩形

力扣刷题day52|84. 柱状图中最大的矩形

文章目录84. 柱状图中最大的矩形思路动态规划单调栈84. 柱状图中最大的矩形 力扣题目链接 给定 n 个非负整数&#xff0c;用来表示柱状图中各个柱子的高度。每个柱子彼此相邻&#xff0c;且宽度为 1 。 求在该柱状图中&#xff0c;能够勾勒出来的矩形的最大面积。 示例 1: …
阅读更多...
空间域图像增强处理-含Labview程序

空间域图像增强处理-含Labview程序

⭕⭕ 目 录 ⭕⭕✳️ 一、引言✳️ 二、领域图像增强实例分析✳️ 2.1 线性滤波实例分析✳️ 2.2 非线性滤波实例分析✳️ 2.3 Canny边缘检测✳️ 三、Labview程序获取✳️ 一、引言 图像在其采集或传递过程中常会受到各种噪声的影响&#xff0c;这会导致其中包含的重要信息很…
阅读更多...
忘机工尺谱 - 快速打谱软件

忘机工尺谱 - 快速打谱软件

引言 为了实现高效快速打谱&#xff0c;我实现了一种词谱分离的输入方案&#xff0c;解决了当前工尺谱平台打谱过程频繁切换输入法和频繁点击鼠标等问题&#xff0c;大大提高了打谱效率。同时借鉴了Markdown编辑器”所见即所得“的思想&#xff0c;输入的同时可以见到排版后的…
阅读更多...
java线程控制

java线程控制

java线程控制的语法很多 这里我们主要说以下三个方法 我们先新建一个包 包下建立两个类 customException 线程类 参考代码如下 public class customException extends Thread {public String name;public customException(){}public void run(){for(int i 0;i < 100;i)…
阅读更多...
逆变器电力计量仪表可安装在分布式光伏运维云平台、光伏变电站

逆变器电力计量仪表可安装在分布式光伏运维云平台、光伏变电站

安科瑞 李可欣 1、概述 AcrelCloud-1200分布式光伏运维云平台通过监测光伏站点的逆变器设备&#xff0c;气象设备以及摄像头设备、帮助用户管理分散在各地的光伏站点。主要功能包括&#xff1a;站点监测&#xff0c;逆变器监测&#xff0c;发电统计&#xff0c;逆变器一次图&…
阅读更多...
解决找不到依赖项的问题（根源直接解决）

解决找不到依赖项的问题（根源直接解决）

&#xff08;文章最后&#xff0c;我会介绍一个万能解决方法&#xff09; 问题&#xff1a; 原因&#xff1a; &#xff08;1&#xff09;可能是你的本地仓库里没有该依赖项。 &#xff08;2&#xff09;如果有的话&#xff0c;可能是没有更新同步到idea 解决方法&#xff1…
阅读更多...
基于Springboot+mybatis+mysql+html教育培训中心教学系统

基于Springboot+mybatis+mysql+html教育培训中心教学系统

基于Springbootmybatismysqlhtml教育培训中心教学系统一、系统介绍二、功能展示1.用户登陆2.用户注册3.个人中心4.人员信息管理5.课程管理6.缴费管理7.学生考勤管理8.器材管理9.问题管理&#xff08;学生、老师&#xff09;一、系统介绍 系统主要功能&#xff1a; 管理员&…
阅读更多...
第五届“传智杯”全国大学生计算机大赛（练习赛）[传智杯 #5 练习赛] 时钟

第五届“传智杯”全国大学生计算机大赛（练习赛）[传智杯 #5 练习赛] 时钟

[传智杯 #5 练习赛] 时钟 题目描述 你有一个电子钟&#xff0c;可以显示 0:00 到 23:59 之间的所有时间&#xff0c;以数字的形式显示。其中小时是 0 到 23&#xff08;0 时会显示一个 0&#xff0c;而 1 到 9 时不会显示前导 0&#xff09;&#xff0c;分钟是 00 到 59&…
阅读更多...
矩阵分析与计算学习记录-矩阵函数

矩阵分析与计算学习记录-矩阵函数

本章重点内容&#xff1a; 矩阵函数的定义和计算 矩阵函数的导数和积分&#xff1a;导数定义和性质、对矩阵变量的导数、矩阵函数的积分及其性质 利用矩阵函数求解线性常系数微分方程&#xff1a;一阶线性常系数微分方程、n阶线性常系数微分方程 1. 矩阵函数的定义和计算 1…
阅读更多...
前端面试总结

前端面试总结

自我检查&#xff1a; 1、 vue有哪些常用的指令 2、 v-if和v-show的区别? v-show 控制的哪个css元素?v-if和v-show初始条件都为false的时候哪个会加载? 3、 3.Vue常用的修饰符? .sync 怎么在子组件触发修改父组件属性的值?具体是$emit哪个事件触发修改? .sync 的原理有了…
阅读更多...
栈的应用----括号匹配问题

栈的应用----括号匹配问题

1.题目 括号匹配 给定一个只包括 ‘(’&#xff0c;‘)’&#xff0c;‘{’&#xff0c;‘}’&#xff0c;‘[’&#xff0c;‘]’ 的字符串 s &#xff0c;判断字符串是否有效。 有效字符串需满足&#xff1a; 左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合…
阅读更多...
Linux常见指令与shell理解

Linux常见指令与shell理解

Linux常用指令与shell理解 文章目录Linux常用指令与shell理解1. ls指令2. cd指令3. pwd命令4. touch指令5. mkdir指令6. rmdir和rm指令7. man指令8. cp指令9. mv指令10. cat与tac指令11. more指令12. less指令13. head指令14. tail指令15. 时间指令16. Cal指令17. find指令18. …
阅读更多...
[附源码]SSM计算机毕业设计置地房屋租赁信息系统JAVA

[附源码]SSM计算机毕业设计置地房屋租赁信息系统JAVA

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
2E服务-WriteDataByIdentifier

2E服务-WriteDataByIdentifier

诊断协议那些事儿 诊断协议那些事儿专栏系列文章&#xff0c;本文介绍数据传输服务下的2E服务WriteDataByIdentifier&#xff0c;允许客户端在通过提供的dataidentifier数据标识符指定的内部位置将信息写入服务器。 参考文章&#xff1a; 数据传输功能单元——DID参数定义 2…
阅读更多...
汇编语言与微机原理 期末复习题整理（大题）

汇编语言与微机原理 期末复习题整理（大题）

写出实现下列计算的指令序列。&#xff08;假定X、Y、Z、W、R都为有符号字变量&#xff09; Z 2*&#xff08;W-X&#xff09;/&#xff08;5*Y&#xff09; ;因为(5*Y)会出现32位变量&#xff0c;32位变量不能作为除数&#xff0c;所以需要改变运算顺序 MOV AX,W ;AX←W S…
阅读更多...
【算法05】合并两个有序链表

【算法05】合并两个有序链表

目录 问题 思路 版本一 版本二 答案 版本一 版本二 问题 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 示例 1&#xff1a; 输入&#xff1a;l1 [1,2,4], l2 [1,3,4] 输出&#xff1a;[1,1,2,3,4,4] 示例二&a…
阅读更多...
[附源码]java毕业设计球队管理系统论文

[附源码]java毕业设计球队管理系统论文

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023