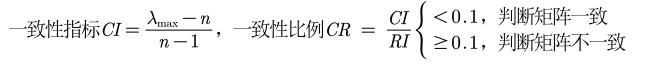层次分析法——评价类问题

原理

1. 首先确定评价的目标，可选方案，评价准则（如何确定评价表格）
在这里插入图片描述

同颜色的单元格的和为1，它们表示的针对某一因素所占的权重(或得分)。

2. 确定权重和每个方案对应指标的得分（如何科学的填写上述的表格）
在这里插入图片描述

解决方法：两个两个指标进行比较，最终根据两两比较的结果来推算出权重
在这里插入图片描述
依据上表填写判断矩阵
判断矩阵是正负反矩阵：主对角线元素为1，关于主对角线对称的位置乘积为1.

按照上述构造的矩阵可能会发生逻辑上的矛盾(不一致), 因此我们需要进行一致性检验。（一致性矩阵的各行各列之间成倍数关系）

3.一致性检验步骤

4. 根据判断矩阵计算权重

5 . 根据权重矩阵计算得分，并进行排序。

代码

disp('请输入判断矩阵A')
A=input('A=');
[n,n] = size(A);
% % % % % % % % % % % % %方法1： 算术平均法求权重% % % % % % % % % % % % %
Sum_A = sum(A);
SUM_A = repmat(Sum_A,n,1);
Stand_A = A ./ SUM_A;

disp('算术平均法求权重的结果为：');
disp(sum(Stand_A,2)./n)
% % % % % % % % % % % % %方法2： 几何平均法求权重% % % % % % % % % % % % %
Prduct_A = prod(A,2);
Prduct_n_A = Prduct_A .^ (1/n);
disp('几何平均法求权重的结果为：');
disp(Prduct_n_A ./ sum(Prduct_n_A))
% % % % % % % % % % % % %方法3： 特征值法求权重% % % % % % % % % % % % %
[V,D] = eig(A);
Max_eig = max(max(D));
[r,c]=find(D == Max_eig , 1);
disp('特征值法求权重的结果为：');
disp( V(:,c) ./ sum(V(:,c)) )
% % % % % % % % % % % % %下面是计算一致性比例CR的环节% % % % % % % % % % % % %
CI = (Max_eig - n) / (n-1);
RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];  %注意哦，这里的RI最多支持 n = 15
% 这里n=2时，一定是一致矩阵，所以CI = 0，我们为了避免分母为0，将这里的第二个元素改为了很接近0的正数
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
    disp('因为CR<0.10，所以该判断矩阵A的一致性可以接受!');
else
    disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
end

插值算法

原理

数模比赛中，常常需要根据已知的函数点进行数据、模型的处理和分析，而有时候现有的数据是极少的，不足以支撑分析的进行，这时就需要使用一些数学的方法，“模拟产生”一些新的但又比较靠谱的值来满足需求，这就是插值的作用。
插值算法还可以用于短期预测（不推荐）

代码

% 分段三次埃尔米特插值
x = -pi:pi; y = sin(x); 
new_x = -pi:0.1:pi;
p = pchip(x,y,new_x);
figure(1); % 在同一个脚本文件里面，要想画多个图，需要给每个图编号，否则只会显示最后一个图哦~
plot(x, y, 'o', new_x, p, 'r-')

% plot函数用法:
% plot(x1,y1,x2,y2) 
% 线方式： - 实线 :点线 -. 虚点线 - - 波折线 
% 点方式： . 圆点  +加号  * 星号  x x形  o 小圆
% 颜色： y黄； r红； g绿； b蓝； w白； k黑； m紫； c青


% 三次样条插值和分段三次埃尔米特插值的对比
x = -pi:pi; 
y = sin(x); 
new_x = -pi:0.1:pi;
p1 = pchip(x,y,new_x);   %分段三次埃尔米特插值
p2 = spline(x,y,new_x);  %三次样条插值
figure(2);
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')
legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast')   %标注显示在东南方向
% 说明：
% LEGEND(string1,string2,string3, …)
% 分别将字符串1、字符串2、字符串3……标注到图中，每个字符串对应的图标为画图时的图标。
% ‘Location’用来指定标注显示的位置


% n维数据的插值
x = -pi:pi; y = sin(x); 
new_x = -pi:0.1:pi;
p = interpn (x, y, new_x, 'spline');
% 等价于 p = spline(x, y, new_x);
figure(3);
plot(x, y, 'o', new_x, p, 'r-')

% 人口预测（注意：一般我们很少使用插值算法来预测数据，随着课程的深入，后面的章节会有更适合预测的算法供大家选择，例如灰色预测、拟合预测等）
population=[133126,133770,134413,135069,135738,136427,137122,137866,138639, 139538];
year = 2009:2018;
p1 = pchip(year, population, 2019:2021)  %分段三次埃尔米特插值预测
p2 = spline(year, population, 2019:2021) %三次样条插值预测
figure(4);
plot(year, population,'o',2019:2021,p1,'r*-',2019:2021,p2,'bx-')
legend('样本点','三次埃尔米特插值预测','三次样条插值预测','Location','SouthEast')

在这里插入图片描述

拟合算法

原理

与插值问题不同，在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数（曲线），使得该曲线在某种准则下与所有的数据点最为接近，即曲线拟合的最好（最小化损失函数）
在这里插入图片描述
一、SSE(和方差)
该统计参数计算的是拟合数据和原始数据对应点的误差的平方和，计算公式如下

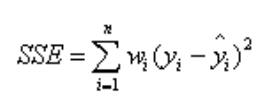
（这个权重没有特殊说明全部取1）
SSE越接近于0，说明模型选择和拟合更好，数据预测也越成功。接下来的MSE和RMSE因为和SSE是同出一宗，所以效果一样

二、MSE(均方差)
该统计参数是预测数据和原始数据对应点误差的平方和的均值，也就是SSE/n，和SSE没有太大的区别，计算公式如下
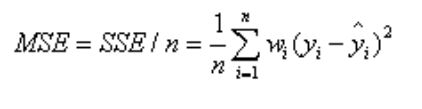
在这里插入图片描述

三、RMSE(均方根)
该统计参数，也叫回归系统的拟合标准差，是MSE的平方根，就算公式如下
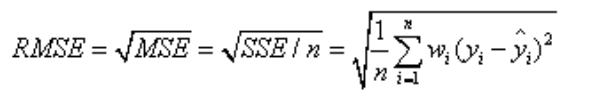
在这里插入图片描述

在这之前，我们所有的误差参数都是基于预测值(y_hat)和原始值(y)之间的误差(即点对点)。从下面开始是所有的误差都是相对原始数据平均值(y_ba)而展开的(即点对全)!

四、R-square(确定系数)
在讲确定系数之前，我们需要介绍另外两个参数SSR和SST，因为确定系数就是由它们两个决定的
(1)SSR：Sum of squares of the regression，即预测数据与原始数据均值之差的平方和，公式如下
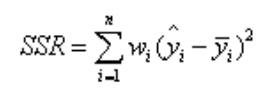
在这里插入图片描述

(2)SST：Total sum of squares，即原始数据和均值之差的平方和，公式如下
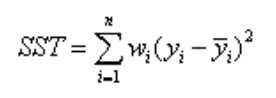
在这里插入图片描述

SST=SSE+SSR，而我们的“确定系数”是定义为SSR和SST的比值，故
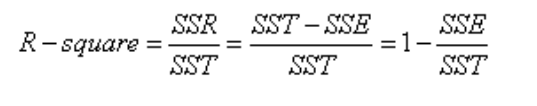
在这里插入图片描述

其实“确定系数”是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0 1]，越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好

代码

用拟合工具箱进行人口预测

工具箱提供的拟合类型有：
Custom Equations：用户自定义的函数类型
Exponential：指数逼近，有2种类型， aexp(bx) 、 aexp(bx) + cexp(dx)
Fourier：傅立叶逼近，有7种类型，基础型是 a0 + a1cos(xw) + b1sin(xw)
Gaussian：高斯逼近，有8种类型，基础型是 a1exp(-((x-b1)/c1)^2)
Interpolant：插值逼近，有4种类型，linear、nearest neighbor、cubic spline、shape-preserving
Polynomial：多形式逼近，有9种类型，linear ~、quadratic ~、cubic ~、4-9th degree ~
Power：幂逼近，有2种类型，ax^b 、ax^b + c
Rational：有理数逼近，分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~；此外，分子还包括constant型
Smoothing Spline：平滑逼近（翻译的不大恰当，不好意思）
Sum of Sin Functions：正弦曲线逼近，有8种类型，基础型是 a1sin(b1x + c1)
Weibull：只有一种，ab*x^{(b-1)*exp(-a*x}b)

clear;clc
year = 1790:10:2000;
population = [3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];
plot(year,population,'o')
cftool  % 拟合工具箱
% (1) X data 选择 year
% (2) Y data 选择 population
% (3) 拟合方式选择：Custom Equation (自定义方程)
% (4) 修改下方的方框为：x = f(t) = xm/(1+(xm/3.9-1)*exp(-r*(t-1790)))
% (5) 左边的result一栏最上面显示：Fit computation did not converge:即没有找到收敛解，右边的拟合图形也表明拟合结果不理想
% (6) 点击Fit Options，修改非线性最小二乘估计法拟合的初始值(StartPoint), r修改为0.02，xm修改为500 
% 有很多同学有疑惑，初始值为什么要这样设置？我们在未来学习微分方程模型和智能算法的课程时再来给大家介绍这里面蕴含的技巧。
% (7) 此时左边的result一览得到了拟合结果：r = 0.02735, xm = 342.4
% (8) 依次点击拟合工具箱的菜单栏最左边的文件—Generate Code(导出代码到时候可以放在你的论文附录)，可以得到一个未命名的脚本文件
% (9) 在这个打开的脚本中按快捷键Ctrl+S，将这个文件保存到当前文件夹。
% (10) 在现在这个文件中调用这个函数得到参数的拟合值和预测的效果
[fitresult, gof] = createFit(year, population)
t = 2001:2030;
xm = 342.4;   
r =  0.02735;
predictions = xm./(1+(xm./3.9-1).*exp(-r.*(t-1790)));  % 计算预测值（注意这里要写成点乘和点除,这样可以保证按照对应元素进行计算）
figure(2)
plot(year,population,'o',t,predictions,'.')  % 绘制预测结果图

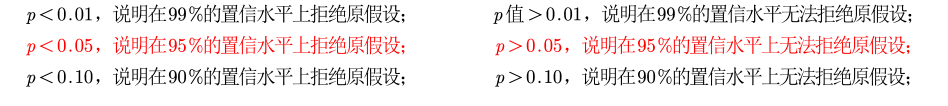
在这里插入图片描述