一,岭回归和LASSO回归

1.1 多重共线性

处理多重共线性最直接的方法是手动移除共线性的变量：即先对数据进行相关分析，若两个特征的相关系数大于某特定值（一般为0.7），则手动移除其中一个特征，再继续做回归分析。

这种做法会导致估计结果产生偏差，会引起遗漏变量问题。而且有时数据特征本来就很少，或并不想直接删除特征，此时可考虑其他更加有效的方法。

岭回归(Ridge Regression)是一种改良的最小二乘法，其通过放弃最小二乘法的无偏性，以损失部分信息为代价来寻找效果稍差但回归系数更符合实际情况的模型方程该模型求解的回归模型的损失函数为线性最小二乘函数，正则化采用L2-范数。称为岭回归

岭索法合回归(Ridge Regression)与套家回归3((Lasso Regression) 两个算不是为了提升模型表现，而是为了修复漏洞而设计的。

1.2 岭回归接手

从数据发现，自变量身长、自变量头围的VIF值均大于200，VIF指标是非常不错的共线性的指针，一般上，当VIF>10,即可怀疑存在共线性问题了。

也就是说，身长和头围这两个属性/特征存在较为严重的共线性问题。如果强行拟合线性回归的话，模型不可用。但是医师就是要研究身长、头围、体重和周龄的关系，我们还不能直接剔除。
显然普通线性回归已经不合适了，需要使用岭回归。

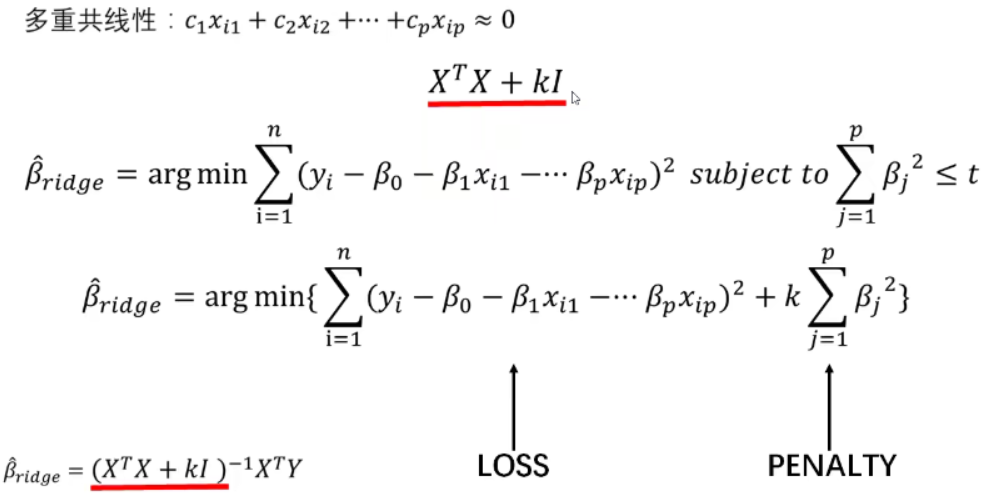
1.3 线性回归的漏洞（线性系数的矛盾解释）

某医师希望通过B超影像里胎儿的身长、头围、体重来预测胎儿周龄，这些观测值均是连续性数值变量，所以很容易想到建立一个多重线性回归方程来解决问题。

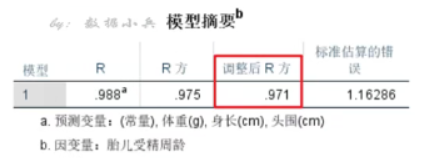
周龄为因变量,体重、身长、头围为自变量的回归方程,调整后R2=0.971,说明模型拟合的不错。

1.4 Ridge Regression

正则化项是参数的L2范数时，回归方法就叫做岭回归。因为权重系数随lambda变化呈山脊状，等于零时为最小二乘。相应损失函数：

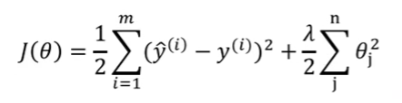
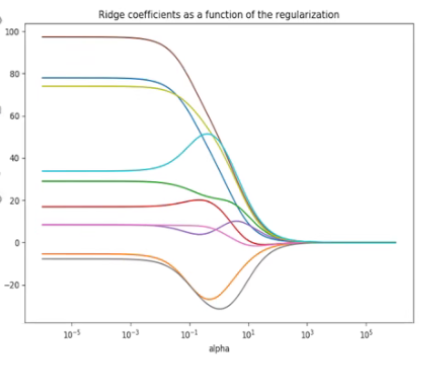
选择lambda的范围意味着要进行最优参数的选择。一般使用岭迹图来判断正则项参数的最佳取值。传统的岭迹图如上图，形似一个开口的喇叭图（根据横坐标的正负，喇叭有可能朝右或者朝左）。正则化参数为横坐标，线性模型求解的权重系数w为纵坐标，每一条彩色的线都是一个系数w，以此来观察正则化参数的变化如何影响了系数w的拟合。岭迹图认为，线条交叉越多，则说明特征之间的多重共线性越高。我们应该选择系数较为平稳的喇叭口所对应的alpha取值作为最佳的正则化参数的取值。

1.5 岭回归实例（加利福尼亚的房价数据集）

1.采用加利福尼亚的房价数据集（事前准备）

from sklearn.datasets import fetch_california_housing
import pandas as pd
housing = fetch_california_housing()
X = housing.data
y = housing.target
df=pd.DataFrame()

2. 循环获取到数据集的特征值：

for i in range(8):
    df[housing["feature_names"][i]]=X[:,i]
df["target"]=y

3.以csv形式存储，然后再拿出来。

df.to_csv("fetch_california_housing.csv",index=None)
df2=pd.read_csv("fetch_california_housing.csv")
pd.set_option('display.max_column', None)

4.输出查看一下：

df.describe()
print(df2)
print(df2.info)
print(df.describe())

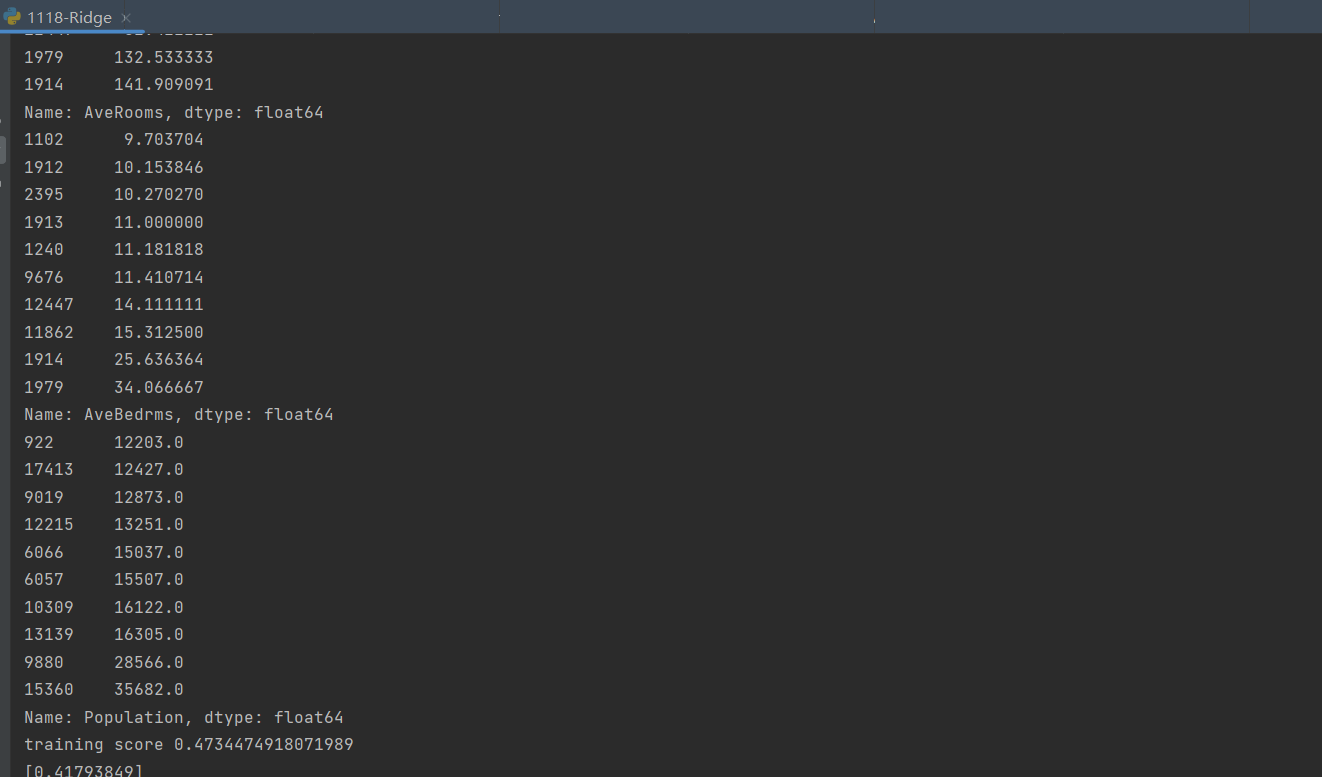
5.盒图

import  matplotlib.pyplot as plt
plt.boxplot(X[:,0],showmeans=True,meanline=True)
plt.show()

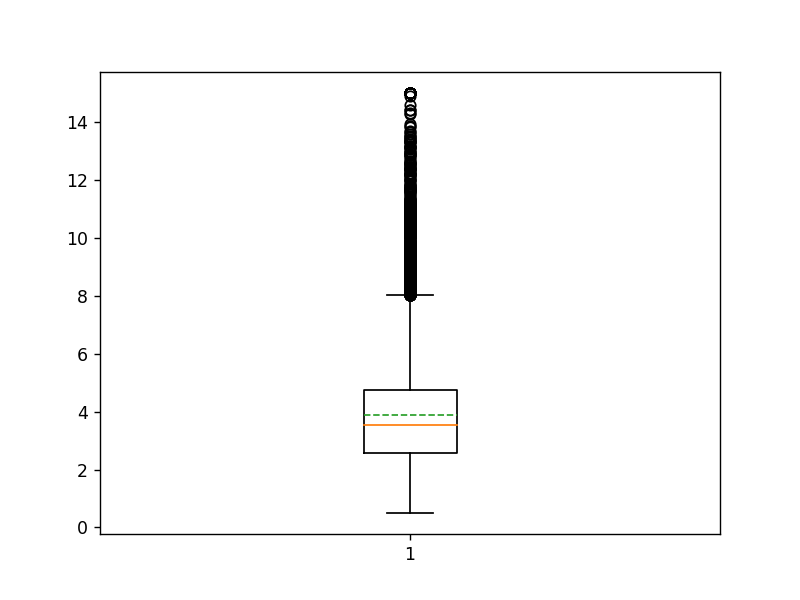
6.线性回归

import matplotlib.pyplot as plt
import numpy as np
plt.scatter(df.iloc[:,:1].values,y,color="red")
plt.scatter(df.iloc[:,:1].values,y)
plt.scatter(df.iloc[:,:1].values,np.dot(df.iloc[:,:1].values,linear.coef_)+linear.intercept_)
plt.show()

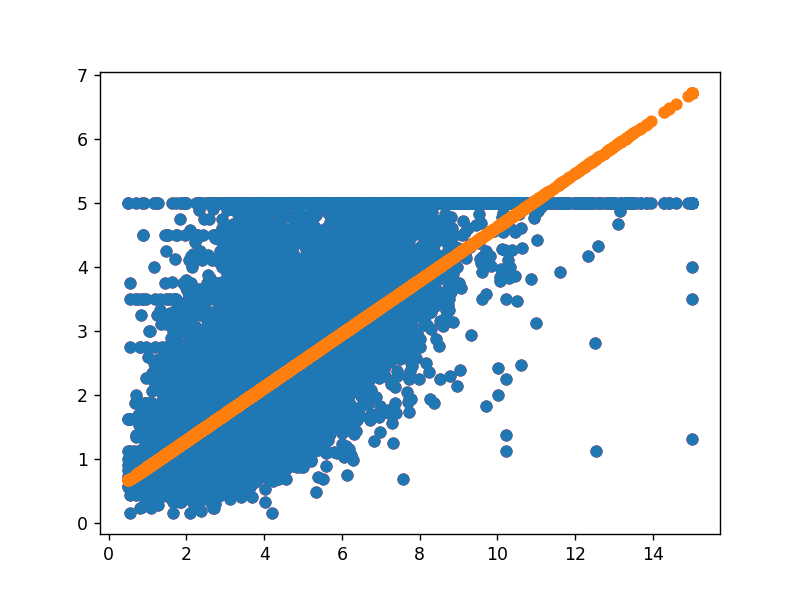
7.岭迹图，使用 sklearn 函数计算：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

plt.figure(figsize=(18, 18))

from sklearn import linear_model
linear = linear_model.Ridge(fit_intercept=False)

def ridgeCalc(dataSet):
    numTestPts = 30
    wMat = np.zeros((numTestPts, dataSet.shape[1]-1))
    for i in range(numTestPts):
        linear.set_params(alpha = np.exp(i-10))
        linear.fit(dataSet.iloc[:, :-1].values, dataSet.iloc[:, -1].values)
        wMat[i,:] = linear.coef_
    return wMat

ridgeWeights = ridgeCalc(df)
plt.plot(ridgeWeights)
plt.xlabel('log(lambda)')
plt.ylabel('weights')
plt.show()

结果如下：

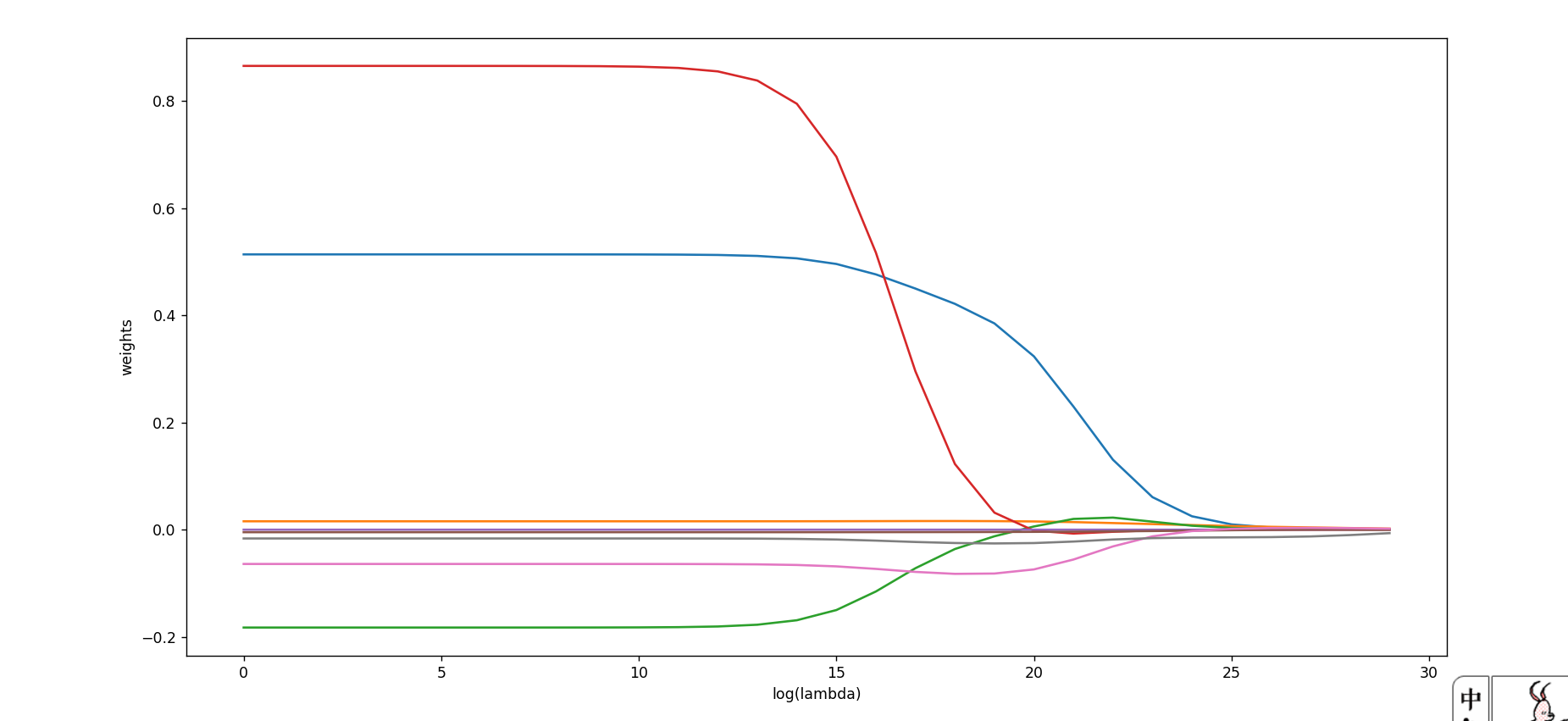
1.6 MSE

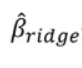是有偏估计,但是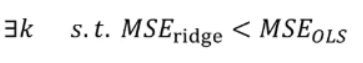

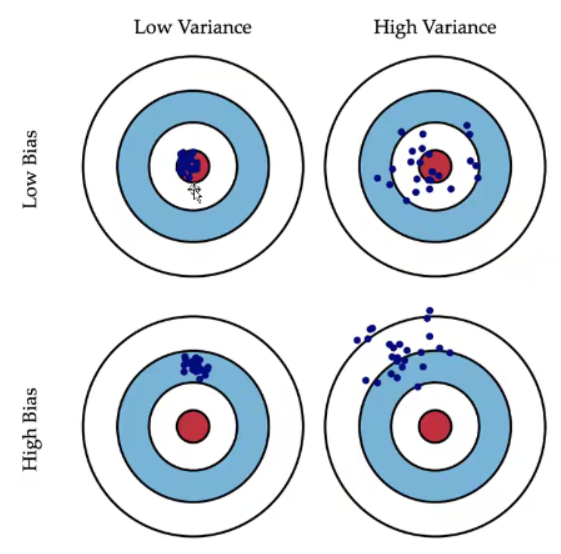
1.7 LASSO

Lasso从根本上来说不是解决多重共线性问题，而是限制多重共线性带来的影响及特征选择工具。

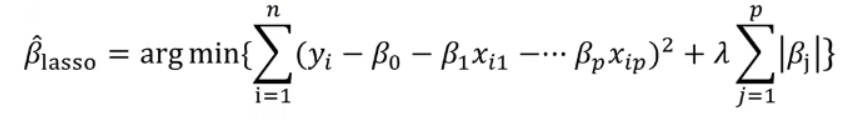
虽然Lasso是为了限制多重共线性，然而我们其实并不使用它来抑制多重共线性，而是发挥其在其他方面的优势。L1和L2正则化一个核心差异就是他们对系数w的影响：
两个正则化都会压缩系数w的大小，对标签贡献更少的特征的系数会更小，也会更容易被压缩。不过，L2正则化只会将系数压缩到尽量接近0，但L1正则化主导稀疏性，因此会将系数压缩到0。这个性质，让Lasso成为了线性模型中的特征选择工具的首选。

左为Lasso 回归，右为岭回归。β1，β2是要优化的模型参数。红色椭圆为目标函数,蓝色区域是解空间

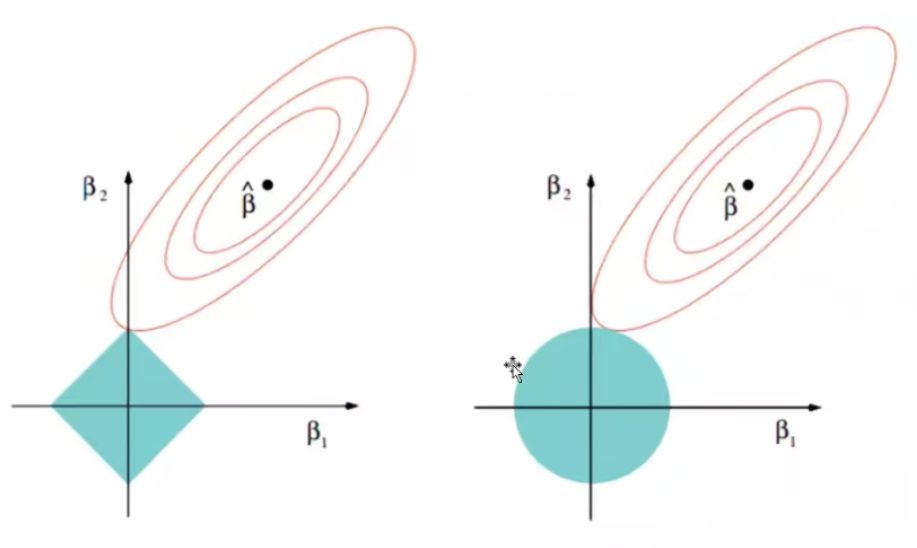
1.8 Ridge岭回归和Lasso套索回归的比较

无论岭回归还是Lasso回归， 本质都是通过调节入来实现模型误差和方差的平衡调整。红色的椭圆和蓝色的区域的切点就是目标函数的最优解。
可划二个泰相的稳定，.5回比以看出Lasso的最优解更容易切到坐标轴上， 形成稀疏结果(某在机器学习中，面对海量的数据，首先需要降维，争取用尽可能一少些>的数据解决问题， Lasso方法可以将特征的系数进行压缩并使某系数变为0.进而达到特征选择的目的，尔可以广泛地应用三模型改进与选择。

1.9 Lasso套索回归实例（红酒数据集）

1.采用load_wine红酒数据集：

from sklearn.datasets import load_wine
import pandas as pd
wine = load_wine()
X=wine.data
y=wine.target
df=pd.DataFrame()

2. 十三组数据集：

for i in range(13):
    df[wine["feature_names"][i]]=X[:,i]
df["target"]=y
pd.set_option('display.max_column', None)
df.describe()

3.岭迹图，使用 sklearn 函数计算

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

plt.figure(figsize=(18, 18))

from sklearn import linear_model
linear = linear_model.Ridge(fit_intercept=False)

def ridgeCalc(dataSet):
    numTestPts = 30
    wMat = np.zeros((numTestPts, dataSet.shape[1]-1))
    for i in range(numTestPts):
        linear.set_params(alpha = np.exp(i-10))
        linear.fit(dataSet.iloc[:, :-1].values, dataSet.iloc[:, -1].values)
        wMat[i,:] = linear.coef_
    return wMat

ridgeWeights = ridgeCalc(df)
plt.plot(ridgeWeights)
plt.xlabel('log(lambda)')
plt.ylabel('weights')
plt.show()

运行结果如下：

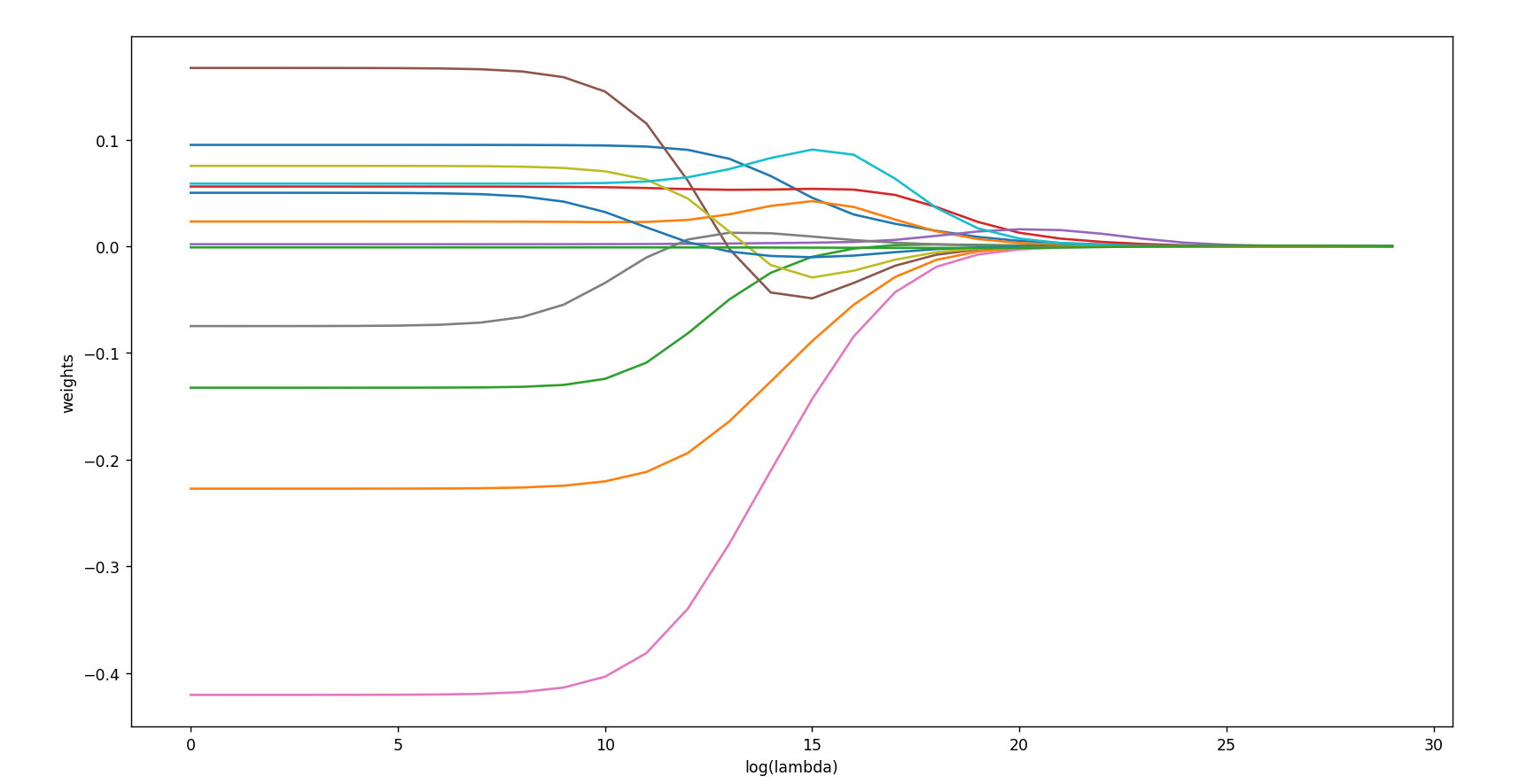
4. Lasso 特征选择
   • 按列归一化，使用 zero-score 零均值归一化算法

wine_X = X.copy()
for i in range(X.shape[1]):
    column_X = X[:, i]
    wine_X[:, i] = (column_X - column_X.mean())/column_X.std()

5.Lasso 回归

from sklearn import linear_model
model = linear_model.Lasso(alpha=np.exp(7-10), fit_intercept=False)
model.fit(wine_X, y)
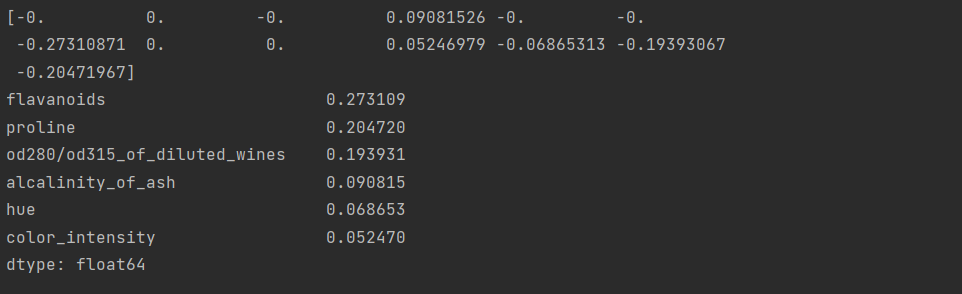
print(model.coef_)

coef = pd.Series(model.coef_, index=df.drop('target', axis=1, inplace=False).columns)
print(coef[coef != 0].abs().sort_values(ascending = False))