题目描述

有一条宽度为 $n$ 的河流。河的左岸是 $0$ 单元格，右岸是 $n+1$ 单元格(更正式地说，这条河可以表示为一串从 $0$ 到 $n+1$ 编号，一共 $n+2$ 单元格)。河上还有 $m$ 个木制平台，其中 $i$ 个平台的长度为 $c_i$ (因此 $i$ 个平台占用了河上 $c_i$ 个连续的单元格)。可以保证平台长度之和不超过 $n$ 。

您现在站在 $0$ 处，并希望以某种方式到达 $n+1$ 。如果您站在位置 $x$ 上，您可以跳到范围 $[x+1,x+d]$ 中的任意位置。但是你并不喜欢水，所以你只能跳到属于某个木制平台的单元格。例如，如果是 $d=1$ ，您只能跳到下一个位置(如果它属于木制平台)。您可以假设单元格 $0$ 和 $n+1$属于木质平台。

您想知道的是，如果您可以将任意平台向左或向右移动任意次数(可能是零)，只要它们不相交(但两个平台可以相碰)，那么是否有可能从 $0$ 到达 $n+1$ 。这也意味着您不能改变平台的相对顺序。
注意，在开始跳跃之前，应先移动平台(换句话说，先移动平台，然后开始跳跃)。

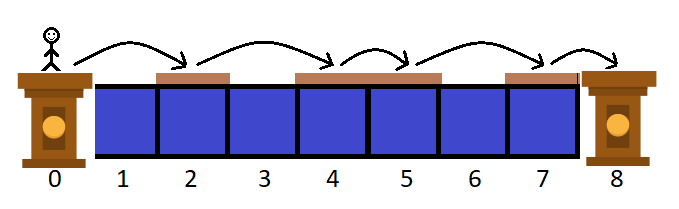
例如，如果有 $n=7$ 、 $m=3$ 、 $d=2$ 和 $c=[1,2,1]$ ，那么从 $0$ 到达 $8$ 的方法之一是遵循以下步骤：
$$n=7$$

输入格式

输入的第一行包含三个整数 $n、m$ 和 $d(1\le n,m,d\le 1000,m\le n)$，分别是河流的宽度、平台的数量和跳跃的最大距离。

输入的第二行包含 $m$ 个整数，$c_1,c_2,...,c_m(1\le c_i\le n,\sum _{i=1}^m{c}_i\le n)$，其中 $c_i$ 是 第 $i$ 个平台的长度。

输出格式

如果无法从 $0$ 到达 $n+1$ ，则在第一行打印 NO。否则，第一行打印 YES，第二行打印长度为 $n$ 的数组 $a$ - 河单元格序列(不包括单元格 $0$ 和单元格 $n+1$ )。

如果单元格 $i$ 不属于任何平台，则 $a_i$ 应为 $0$ 。否则， $a_i$ 应等于单元格 $i$ 所属平台的索引( 平台按输入顺序从 $1$ 到 $m$ 编号)。

注意所有等于 $1$ 的 $a_i$ 应构成长度为 $c_1$ 的数组 $a$ 的连续子块，所有等于 $2$ 的 $a_i$ 应构成长度为 $c_2$ 的数组 $a$ 的连续子块，…，所有等于 $m$ 的 $a_i$ 应构成长度为 $c_m$ 的数组 $a$ 的连续子块。 $a$ 中 $2$ 的最左端位置应大于 $1$ 的最右端位置， $a$ 中 $3$ 的最左端位置应大于 $2$ 的最右端位置，…， $a$ 中 $m$ 的最左端位置应大于 $m?1$ 的最右端位置。

样例输入1

7 3 2
1 2 1

样例输出1

YES
0 1 0 2 2 0 3 

样例输入2

10 1 11
1

样例输出2

YES
0 0 0 0 0 0 0 0 0 1 

样例输入3

10 1 5
2

样例输出3

YES
0 0 0 0 1 1 0 0 0 0 

提交链接

https://hydro.ac/d/lp728/p/15

提示

请看第一个例子：答案是 $[0,1,0,2,2,0,3]$ 。你执行的跳跃序列是 $0\to 2\to 4\to 5\to 7\to 8$ 。

再看第二个例子：如何放置平台并不重要，因为你总是可以从 $0$ 跳到 $11$ 。

再看第三个例子：答案是 $[0,0,0,0,1,1,0,0,0,0]$。你的跳跃顺序是 $0\to 5\to 6\to 11$ 。

解析

此题的难点在于输出木板的位置。若单纯的判断是否能够到达，是比较简单的，直接每次跳跃最大距离。

现在每次跳跃最大距离可能导致木板没有办法放置。处理的办法，先把所有的木板按顺序放置再右边，同时记录编号。

$now$ 记录当前的位置，若前面有木板，先走到木板的右边再开始跳，每次跳跃最大距离，落脚点若为水，则移动一个木板到当前的落脚点。

这样操作之后，能保证木板一定是在河流范围内且完美放下。

参考代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 9;
int n , m , d , c[maxn] , plat[maxn];
int main()
{
	cin >> n >> m >> d; //河流的宽度  平台的数量  跳跃的最大距离
	for(int i = 1; i <= m; i++)
		cin >> c[i];  //第i个平台的长度
	/*按顺序，先全部放在右边*/
	int x = n;
	for(int i = m; i >= 1; i--)
	{
		while(c[i])
		{
			plat[x--] = i;
			c[i]--;
		}
	} 
	int now = 0;
	while(1)
	{
		/*走到当前木板的最右边再开始跳，体现贪心*/
		while(now + 1 < n + 1 && plat[now + 1])
			now++;
		if(now + d >= n + 1)
			break;
		/*需要木板,找到最左边木板的左右端点*/
		 
		if(!plat[now + d])
		{
			int lpos = - 1 , rpos;
			for(int i = now + d; i <= n; i++)
			{
				if(plat[i])
				{
					lpos = i;
					break;
				}
			}
			if(lpos == -1)
			{
				cout << "NO";
				return 0;
			}
			for(int i = n; i > now + d; i--)
			{
				if(plat[i] == plat[lpos])
				{
					rpos = i;
					break;
				}
			}	
			while(!plat[now + d])
			{
				swap(plat[rpos] , plat[lpos - 1]);
				rpos--;
				lpos--;
			}
		}
		now += d;
	}
	cout << "YES" << endl;
	for(int i = 1; i <= n; i++)
		cout << plat[i] << " ";
	return 0;
}