这次博主在学习完知识点和代码之后,准备对这个知识重新进行整理总结。站在一个初学者的角度来看待这个知识点,在他人的讲解基础上加一点点自己的理解,并记录下来。以加深自己的理解,并且希望能够帮助到你。博主是一个初学者,若有不对请友善指出,大家一起学习进步。
一、知识点讲解
这里简单地进行说明。
1.为什么使用Morris中序遍历
树的递归使用的是栈这个数据结构来存储节点,以达到记录前驱节点的目的。而过多的内容很可能导致栈溢出。为了压缩空间(降低空间复杂度),所以我们使用Morris中序遍历,能够将空复降至O(1)。(结尾学习视频有更详细的原理解释)
2.什么是Morris中序遍历
既然递归中使用栈的原因是想记录前驱节点,那么我们只要达到记录前驱节点的目的即可不使用栈。
首先,它的本质还是中序遍历。
正常的中序遍历,在“递”左子树时是可以直接通过左指针到达,但是在“归”根节点的时候是没有办法直接到达的(右子树只用“递”,不用“归”)。而“归”的时候均是到达叶子节点才“归”,则可以充分利用叶子节点的左右空指针,将右空指针指向根节点,这样就可以直接“归”到根节点。
其中,为什么是右空节点呢?博主认为,因为根节点是叶子节点的后继节点,而中序遍历遍历完本节点下一个就遍历右节点,所以用叶子节点的右空节点指向根节点。
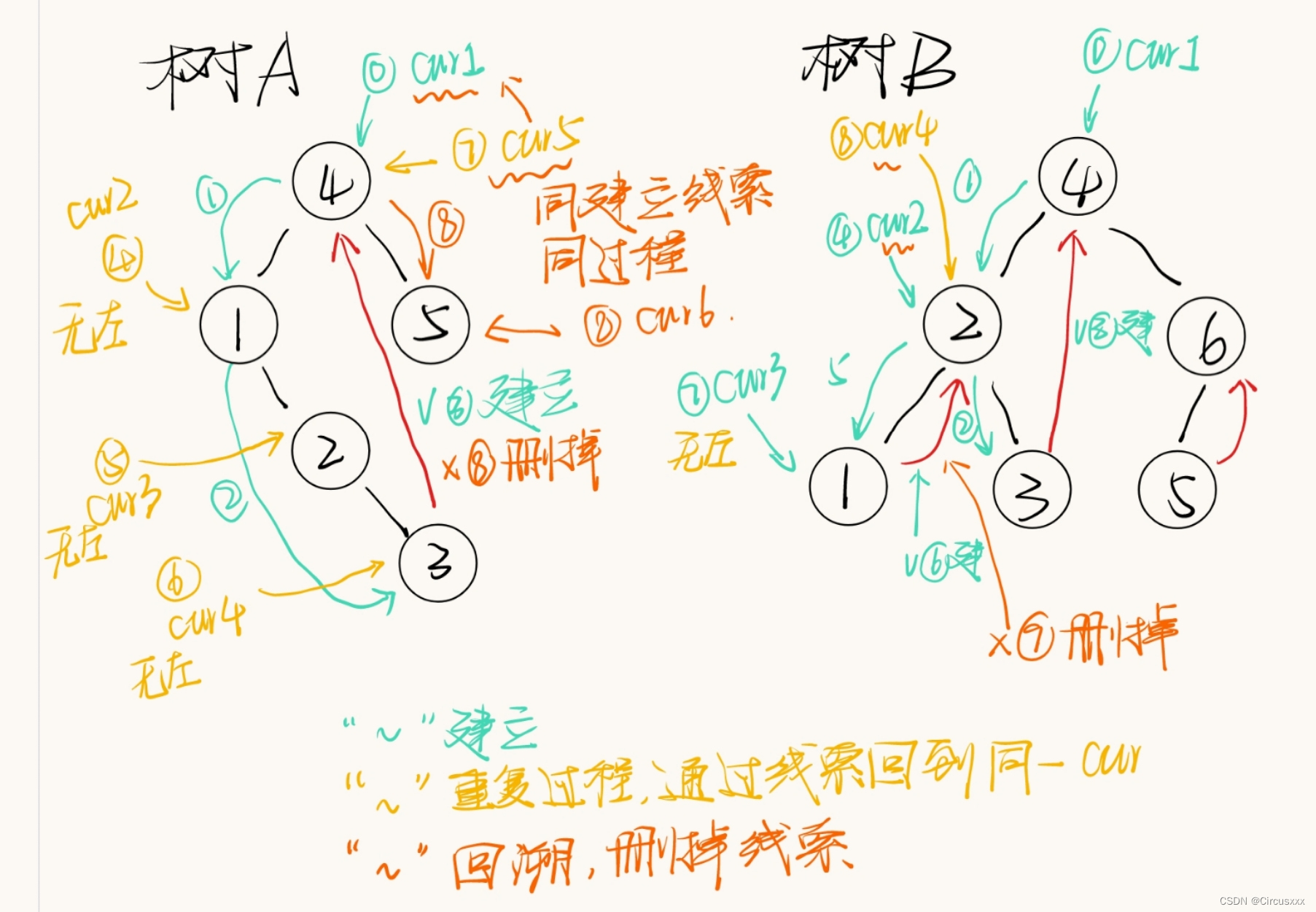
下面结合图进行理解:

其中,序号是按照中序遍历的顺序编号的,方便大家观看。
而红色的线就是我们需要增加的指针,称为线索(也是线索二叉树的由来)。
基本原理理解了,那我们就来看看代码是什么实现的。
二、代码及分析
1.实现代码
代码参考文章末尾学习视频。博主为代码添加了部分注释:
from typing import Optional
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def MorrisInorderTraversal(self, root: Optional[TreeNode]):
# 本质是中序遍历
cur = root
# 遍历节点
while cur:
# 没有左子树
# 当前节点就没有中序遍历前驱节点,直接进入右边
if not cur.left:
cur = cur.right
# 有左子树
# 找cur的中序遍历前驱节点
# 通俗讲,前驱在左节点最右边
else:
pre = cur.left # 左节点
# 到最右边
while pre.right and pre.right != cur:
pre = pre.right
# 跳出循环两种情况
# 情况一:到达最右边
# 建立线索
if pre.right is None:
pre.right = cur
print(f"设置线索:{pre}->{cur}")
# 继续遍历左边
# 中序是遍历完左子树再遍历根
cur = cur.left
# 情况二:遍历完左子树,进行回溯
# 如果没有建立线索的二叉树是不会出现pre.right == cur的
# 说明此处已经建立了线索,已经遍历过了
# 线索二叉树的回溯是通过线索回溯的
else:
pre.right = None # 删掉线索,还原二叉树
print(f"删掉线索:{pre}->{cur}")
# 左边已经遍历完了,遍历右边
cur = cur.right下面对我当时看到代码时产生的疑问进行解答:
问:为什么会有回溯过程?
答:它是一步一步进入左子树进行遍历的。如先进入root的左节点找前驱,再去root.left的左节点找前驱,那么叶子节点已经被建立联系了。当到达叶子节点时,无左节点,在进入右节点时会通过之间建立好的线索进行回溯到上一个节点,再重复建立过程,相当又要经历建立好的线索进行回溯。进而回溯到根节点(每个节点)再进入右子树进行遍历。
另外,删掉线索的那一行代码是可以注释掉的,这样就可以得到遍历后的树,而不是只是经历过程。
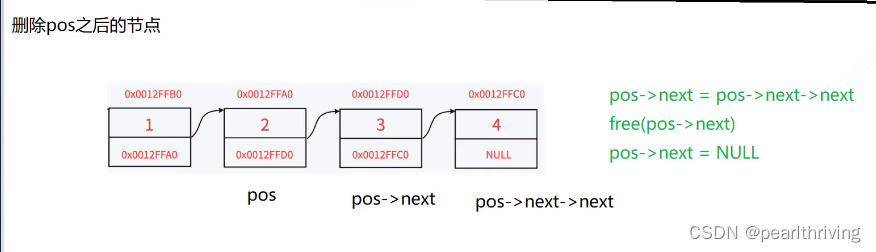
下面结合图片对过程进行理解,主要是理解过程,不必死磕过程。在博主的眼中,树是抽象且局部重复的,我们只需要关注局部,理解对局部的操作即可。
2.对代码进行测试
写完一个代码还是需要对代码进行测试。作为一个初学者,我觉得记录下测试的方法还是很有必要的。
(1)首先要初始化树
学习链接:http://t.csdnimg.cn/P1wB7
具体初始化代码就不写了,对学习链接代码进行修改即可。(ps:需要对树类名,和左右指针名进行修改哦)
另外,其中的运行结果在哪里查看呢?博主搜索后发现在Debug处查看。需要在操作后断点,断点如下:
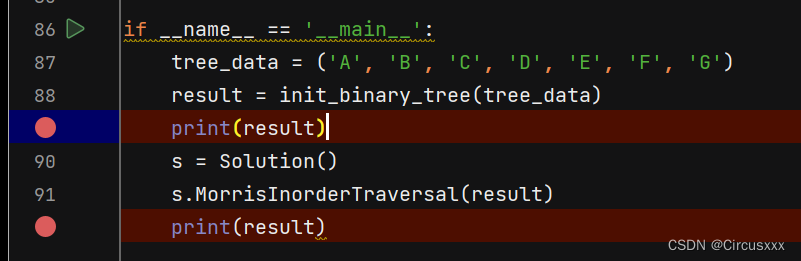
(2)对初始化后的树使用函数即可,再断点查看就行了(如上图第二处断点,记得注释掉删除线索的那一行代码)。
三、使用Morris中序遍历
练习题目:501. 二叉搜索树中的众数
博主是在遇到这道题时才来学习的这个方法,可以通过这道题来练习一下。
四、学习和参考视频
【【算法奇淫技】第1期 Morris遍历(二叉树的特殊遍历法)】 https://www.bilibili.com/video/BV13J411z7Z5/?share_source=copy_web&vd_source=dc0e55cfae3b304619670a78444fd795
完
感谢你看到这里!一起加油吧!



![[CUDA 学习笔记] 矩阵转置算子优化](https://img-blog.csdnimg.cn/direct/c38345741d86487cb9bd70a1204b44a3.png)