一、基本概念
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。 ——摘自百度百科
要理解哈夫曼树,首先需要理解什么是“带权路径长度”
-
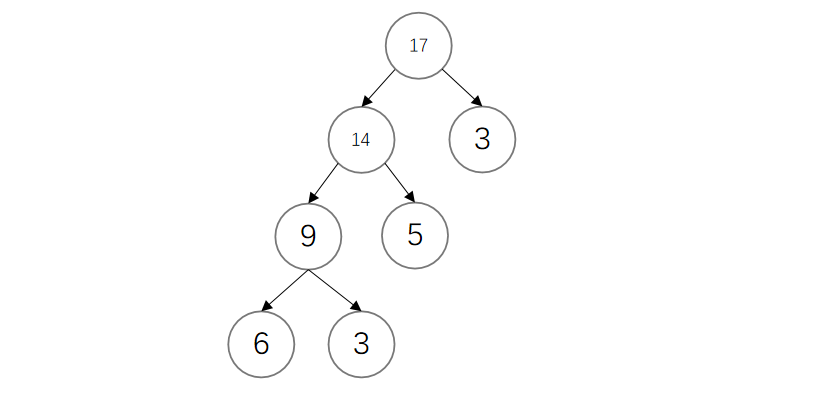
路径:一棵树中一个节点到达其子孙节点之间的通路称为路径。通路中的分支数目称为路径长度。从根节点到第L层节点的路径长度为L-1。例如上面这棵树中,从
17->6的路径长度为3,从14->6的路径长度为2。 -
节点的带权路径长度:从根节点到该节点之间的路径长度与该节点的权的乘积。例如上图中从
17->6的带权路径长度为 3 × 6 = 18 3×6=18 3×6=18。 -
树的带权路径长度:所有叶子节点的带权路径之和。上图的树的带权路径长度为
6+3+5+3=17。
二、构造哈夫曼树
构造一棵哈夫曼树需要如下步骤:
(1)将给定的n个节点看做n棵独立的树(每棵树只有一个节点)
(2)选出权值最小的两棵树作为左右子树合并为一棵树,其根节点的权值为左右子树权值的和
(3)将这两棵树从森林中删除,将新生成的数加入森林
(4)重复(2)(3)步骤直到只剩一棵树
下面通过一个具体的示例演示构造的过程。首先将给定的节点按权值排序:
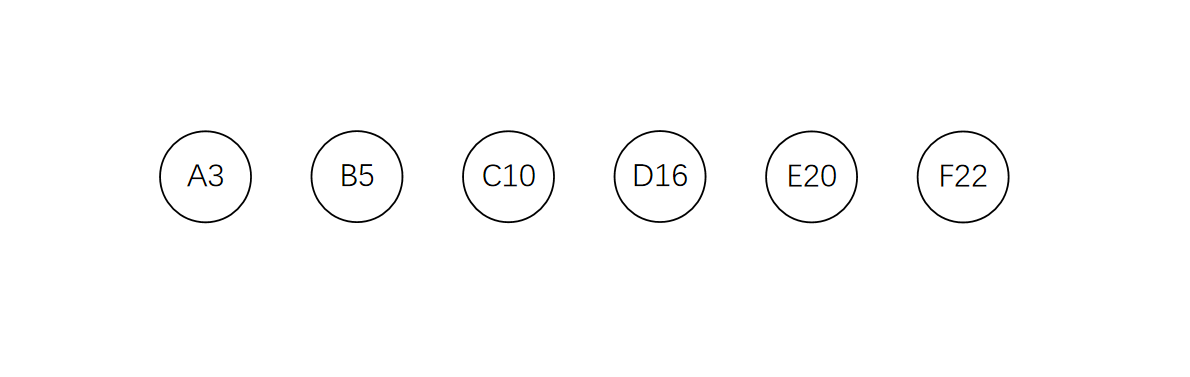
选出其中权值最小的两个节点构成一棵新的树
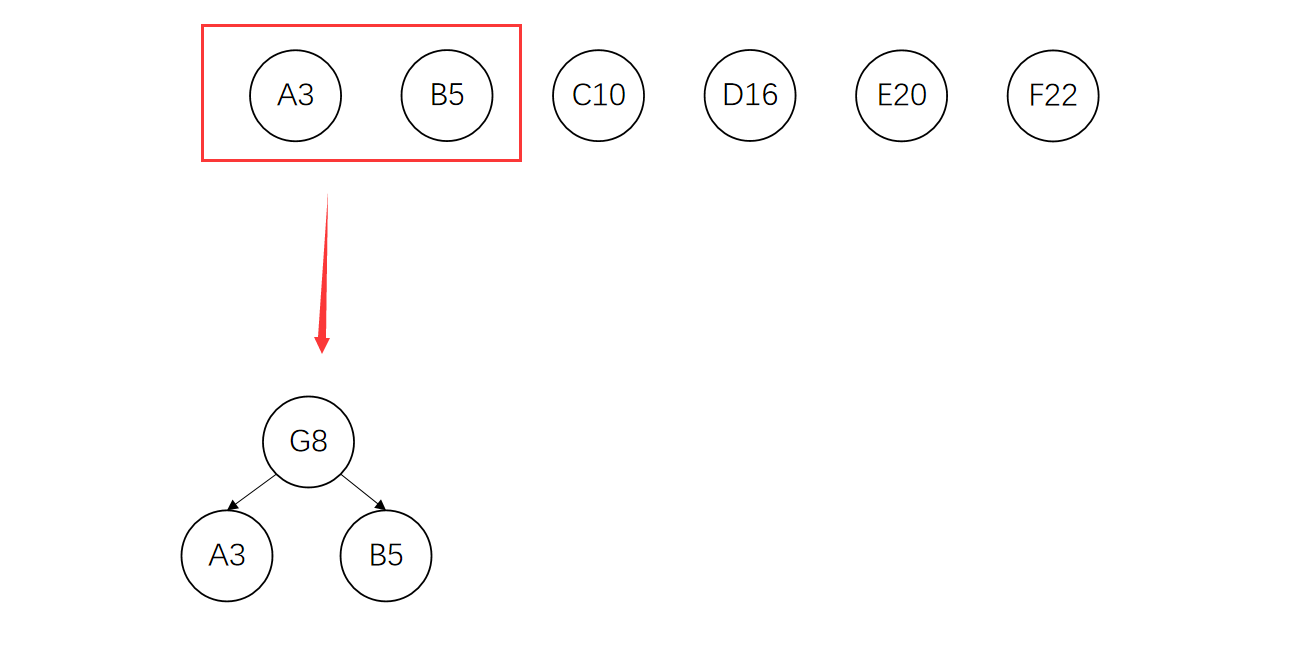
将这两个节点从集合中删除,将新生成的树的根节点加入集合
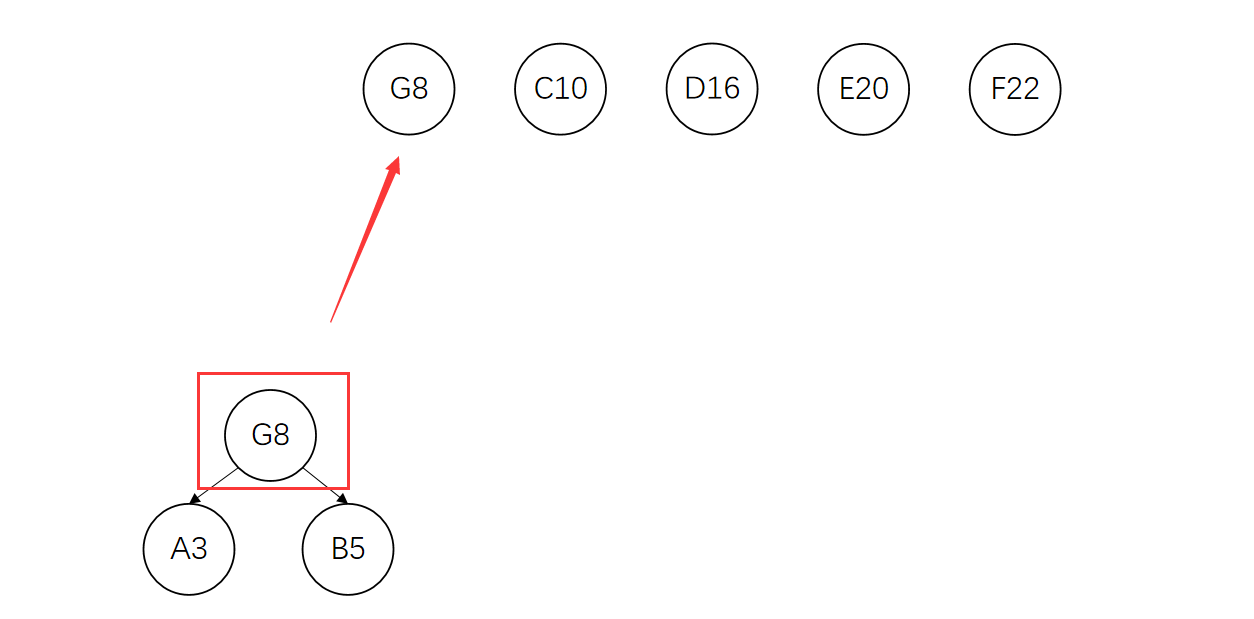
再将G、C节点构成一棵新的树
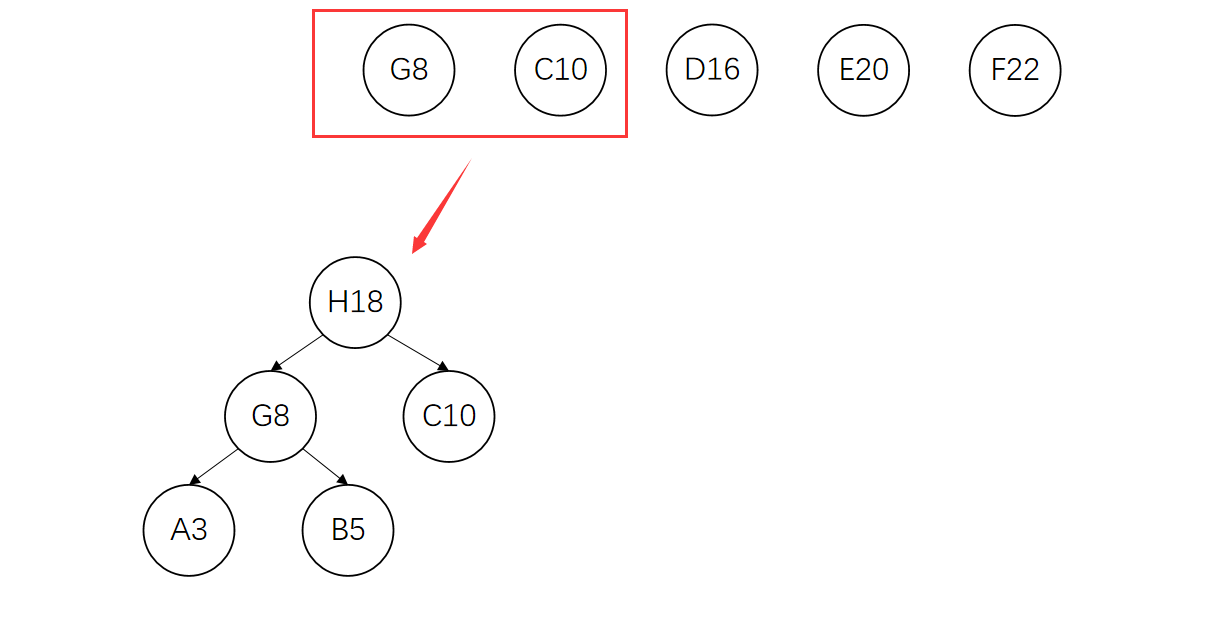
将G、C节点删除,并将新树的根节点H加入集合
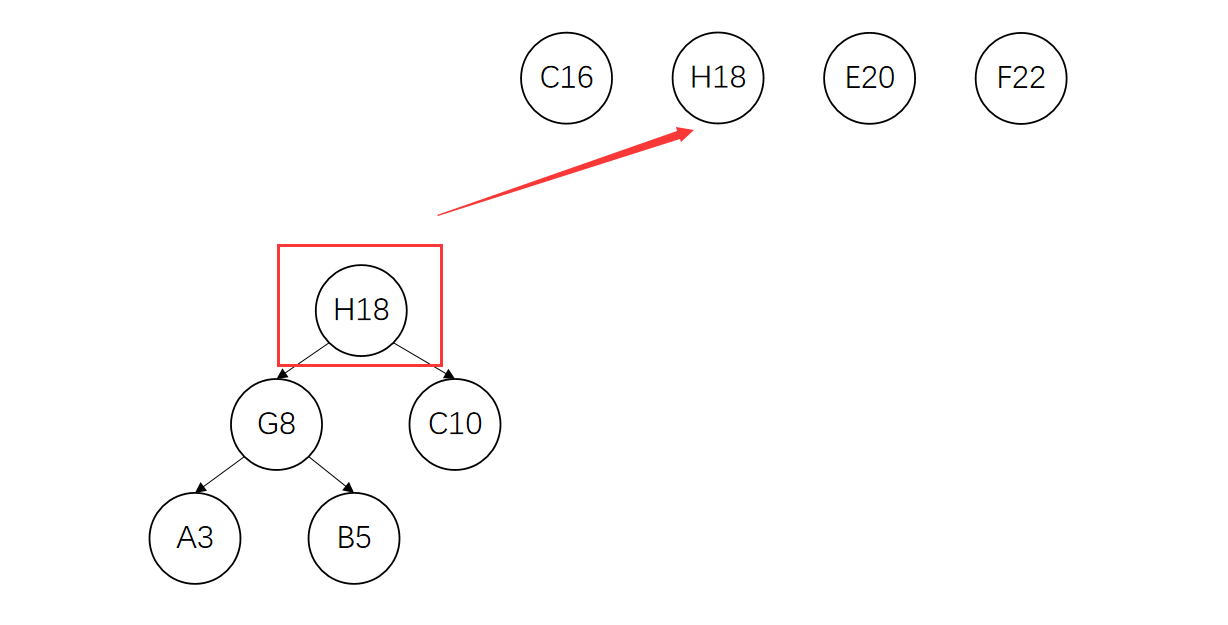
将C、H构造成一棵新的树。因为C节点权值比H小,所以C作为左孩子
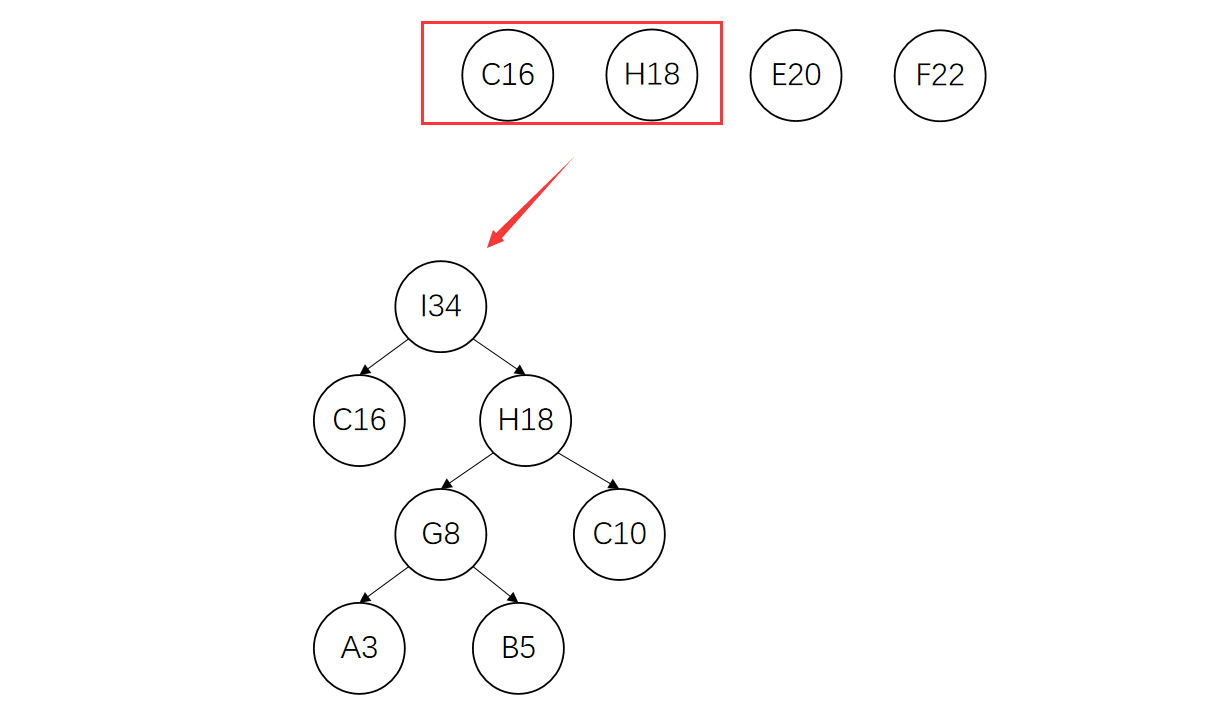
删除C、H,将I加入到集合中
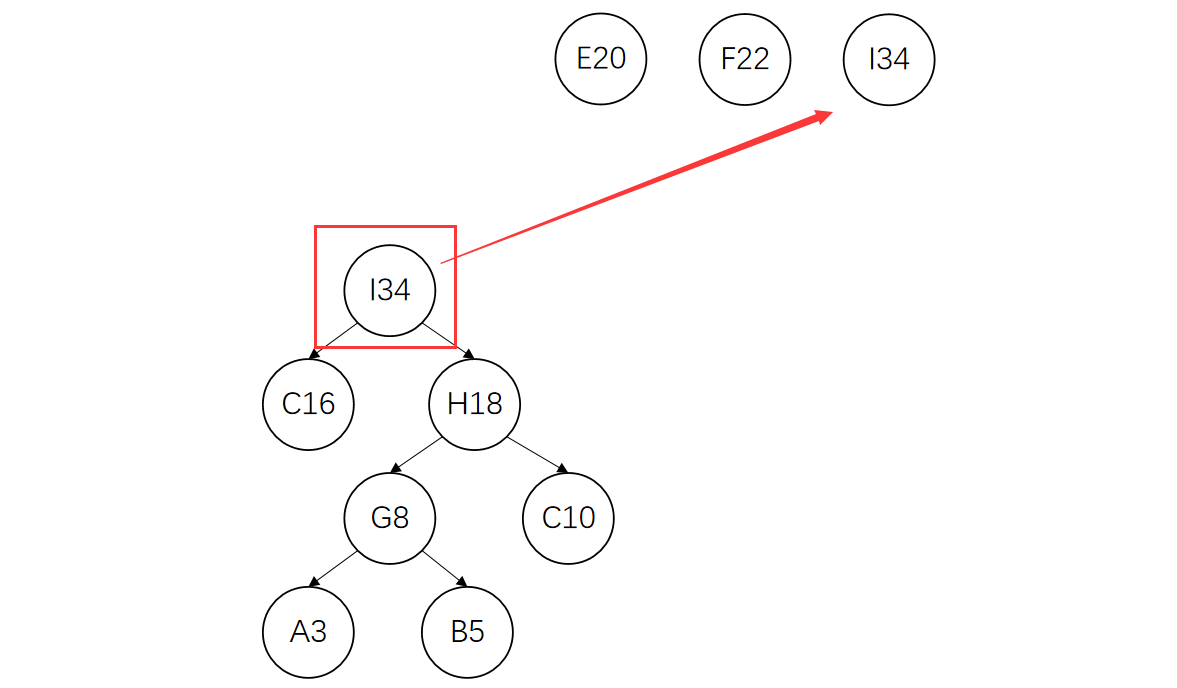
。。。。。。
重复上述过程,直到只剩一棵树,完成哈夫曼树的构造。
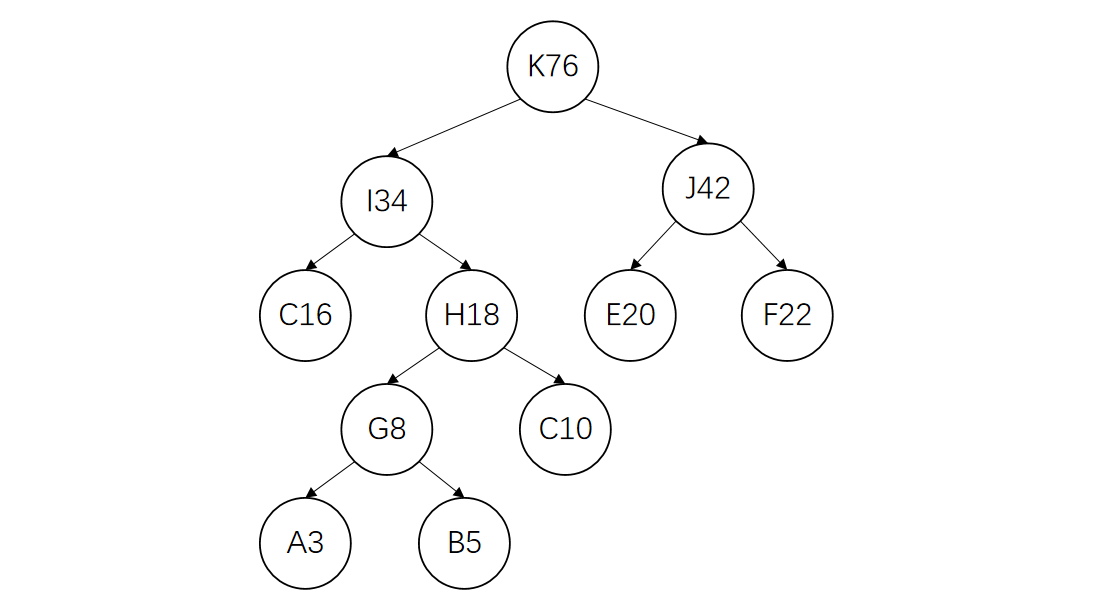
三、代码实现
首先定义出节点的结构
public class TreeNode:IComparable<TreeNode>
{
public int Weight;
public TreeNode? Left;
public TreeNode? Right;
public TreeNode(int weight)
{
Weight = weight;
}
public int CompareTo(TreeNode? other)
{
if (other == null) return 1;
return Weight - other.Weight;
}
}
构造哈夫曼树:
public TreeNode ConstructHuffmanTree(int[] weights)
{
if (weights == null || weights.Length == 0) return null;
HeapList<TreeNode> nodes = new();
foreach (var weight in weights)
{
TreeNode node = new TreeNode(weight);
nodes.Push(node);
}
while (nodes.Count > 1)
{
var left = nodes.Pop();
var right = nodes.Pop();
var head = new TreeNode(left.Weight + right.Weight);
head.Left = left;
head.Right = right;
nodes.Push(head);
}
return nodes[0];
}
这里的HeapList是自己简单实现的一个小根堆,代码如下
public class HeapList<T> where T : IComparable<T>
{
private T[] _items;
// 默认数组大小
private const int DefaultCapacity = 4;
// 元素数量
private int _size;
public int Count => _size;
// 当前数组大小
public int Capacity
{
get => _items.Length;
set
{
if (value < _size)
{
throw new ArgumentOutOfRangeException();
}
if (value != _items.Length)
{
if (value > 0)
{
T[] newItems = new T[value];
if (_size > 0)
{
Array.Copy(_items, newItems, _size);
}
_items = newItems;
}
else
{
_items = new T[DefaultCapacity];
}
}
}
}
public HeapList()
{
_items = new T[DefaultCapacity];
}
public HeapList(int length)
{
_items = new T[length];
}
public T this[int index]
{
get
{
if (index < 0 || index >= _size) throw new ArgumentOutOfRangeException();
return _items[index];
}
}
/// <summary>
/// 压入元素
/// </summary>
/// <param name="e"></param>
public void Push(T e)
{
// 扩容
if (_size >= _items.Length)
{
int newCapacity = _items.Length == 0 ? DefaultCapacity : _items.Length * 2;
if ((uint)newCapacity > Array.MaxLength) newCapacity = Array.MaxLength;
Capacity = newCapacity;
}
_items[_size] = e;
HeapInsert(_size++);
}
/// <summary>
/// 弹出元素
/// </summary>
public T Pop()
{
if (_size <= 0) throw new ArgumentOutOfRangeException();
var node = _items[0];
// 交换首尾元素
(_items[_size - 1], _items[0]) = (_items[0], _items[_size - 1]);
_size--;
// 下沉操作
Heapify(0);
return node;
}
/// <summary>
/// 上浮操作
/// </summary>
/// <param name="index"></param>
private void HeapInsert(int index)
{
// 当前节点比父节点小,交换两者位置
int parentIndex = (index - 1) / 2;
while(_items[index].CompareTo(_items[parentIndex]) < 0 )
{
(_items[index], _items[parentIndex]) = (_items[parentIndex], _items[index]);
index = parentIndex;
parentIndex = (index - 1) / 2;
}
}
/// <summary>
/// 下沉操作
/// </summary>
/// <param name="index"></param>
private void Heapify(int index)
{
// 左孩子节点下标
int left = index * 2 + 1;
while (left < _size)
{
int min = left;
// 左右孩子比较
if (left + 1 < _size && _items[left + 1].CompareTo(_items[left]) < 0)
{
min = left + 1;
}
// 与父节点比较
if (_items[index].CompareTo(_items[min]) < 0)
{
break;
}
// 父节点与子节点交换
(_items[index], _items[min]) = (_items[min], _items[index]);
// 继续向下寻找
index = min;
left = index * 2 + 1;
}
}
}
四、哈夫曼树的应用
研究哈夫曼树最初的目的是为了解决当时的远距离通信数据传输的最优化问题。比如我们有“A”、“B”、“C”、“D”、“E”、“F”六个字母组成的信息。假如将它们用如下二进制表示(图片源自《大话数据结构》)

那么编码后的数据长度将会是字母数×3。
但事实上,组成信息的字母的出现频率可能是不同的。假设这几个字母出现的频率为“A 27,B 8,C 15,D 15,E 30,F 5”,那么我们就可以按照哈夫曼树来规划它们。
首先根据这些字母的权值构建哈夫曼树。再将权值左分支改为0,右分支改为1。(图片源自《大话数据结构》)
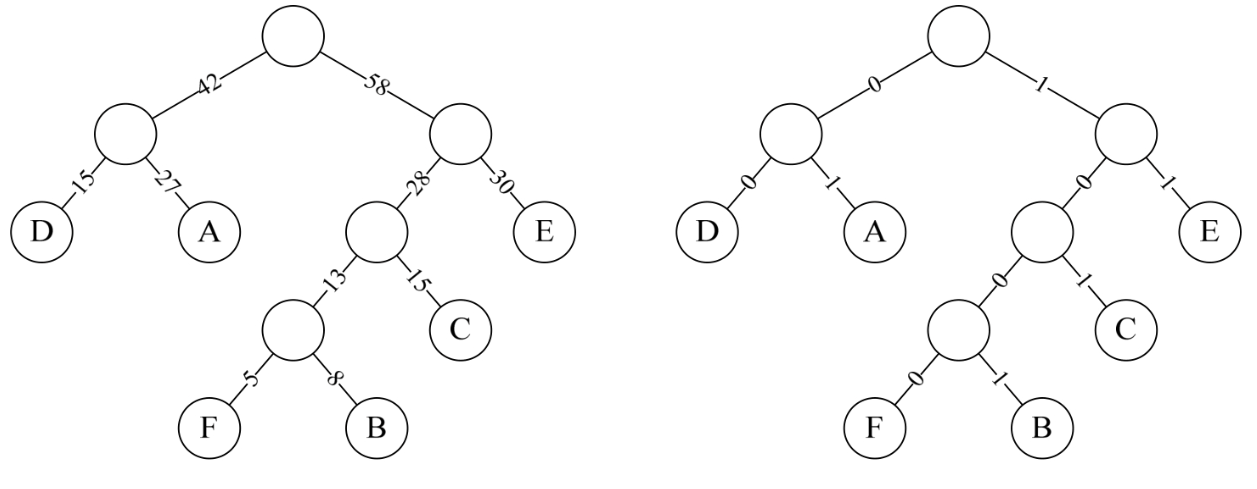
然后按照从根节点到叶子结点所经过的路径,重新对这几个字母进行编码,结果如下(图片源自《大话数据结构》)

我们分别使用上面两种方式对字符串“BADCADFEED”进行编码,可得到如下结果:
原编码方式:001000011010000011101100100011
哈夫曼编码方式:1001010010101001000111100
可以很明显地看出编码长度的减少。当然,在接收方收到数据时,也需要通过相同的哈夫曼树进行解码。
最后总结一下:哈夫曼树实际上是根据节点的权值决定节点在树中的位置。权值较大的节点离根节点越近,权值小的节点离根节点越远。以此来保证从根节点访问时可以更快的到达权值较大的节点,从而达到数据压缩的目的。
五、参考资料
[1].《大话数据结构》
[2].百度百科





![F - Double Chance(期望,数学,树状数组优化)[AtCoder Beginner Contest 276]](https://img-blog.csdnimg.cn/f65b18c5c63a44638aadc92e37752aa5.png)