【POJ No. 3134】幂运算 Power Calculus

POJ 题目地址

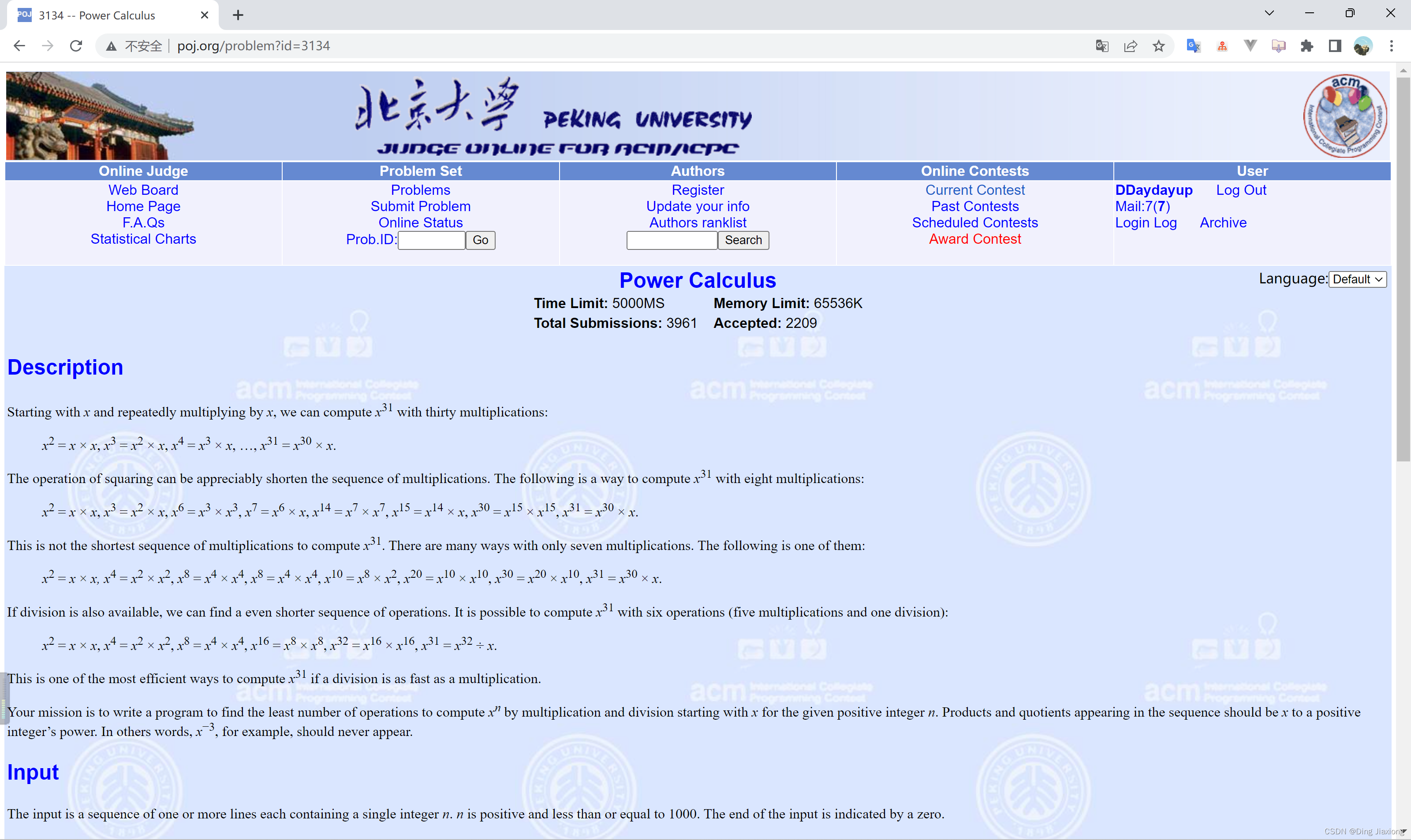
【题意】

从x 开始，反复乘以x ，可以用30次乘法计算x^31

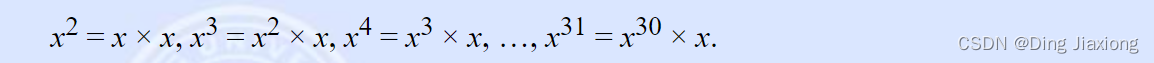
平方运算可以明显地缩短乘法序列，以下是用8次乘法计算x^31 的方
法：

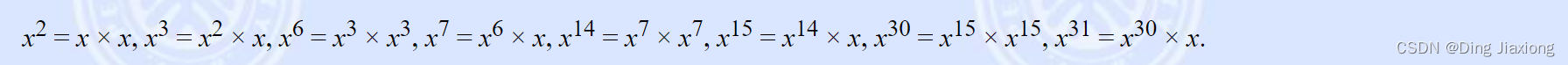
这不是计算x^31 的最短乘法序列。有很多方法只有7次乘法，以下是
其中之一：

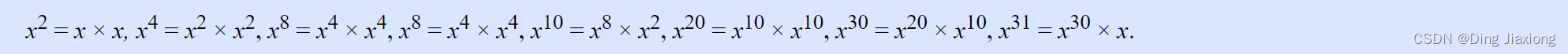
如果除法也可用，则可以找到一个更短的操作序列。可以用6个运
算（5乘1除）计算x^31 ：

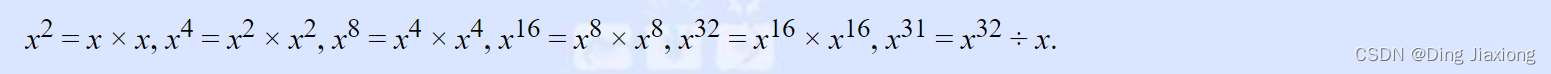
如果除法和乘法一样快，则这是计算x^31 最有效的方法之一。

编写一个程序，通过从x 开始的乘法和除法，为给定的正整数n 找到计算x^n 的最少运算次数。在序列中出现的乘积和商应该是x 的正整数幂。

【输入输出】

输入：

输入是由一行或多行组成的序列，每行都包含一个整数n（0<n ≤1000）。以输入0结束。

输出：

单行输出从x 开始计算x^n 所需的最小乘法和除法总数。

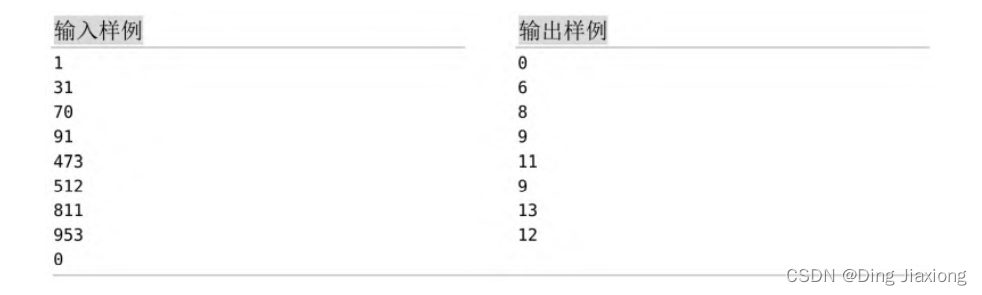
【样例】

【思路分析】

本题从x 开始计算x^n 所需的最小乘法和除法总数，可以采用IDA*算法解决。

【算法设计】

① 初始化，指数ex[0]=1，深度depth=0。

② 进行深度优先搜索，如果ex[d ]=n ，则返回1。如果d≥depth，则返回0。如果当前指数在倍增depth-d 之后还小于n ，则返回0。

③ 从0到d 执行乘法，ex[d +1]=ex[d ]+ex[i ]，深度优先搜索dfs(d +1)，如果成功，则返回1；执行除法，ex[d +1]=abs(ex[d ]-ex[i])，进行深度优先搜索dfs(d +1)，如果成功，则返回1。

④ 如果搜索失败，则深度depth++，重新开始搜索。

【算法实现】

#include<cstdio>
#include<cstdlib>
#include<algorithm>

using namespace std;

int n,depth;
int ex[15];

bool dfs(int d){
	
	if(ex[d]==n) return 1;
	if(d>=depth) return 0;//后面会搜索d+1层 
	if(ex[d]<<(depth-d)<n) return 0;
	for(int i=0;i<=d;i++){
        ex[d+1]=ex[d]+ex[i];//乘法
        if(dfs(d+1)) return 1;
        ex[d+1]=abs(ex[d]-ex[i]);//除法
        if(dfs(d+1)) return 1;
    }
    
    return 0;
}

void IDAstar(){
	ex[0]=1;
	for(depth=0;;depth++){
		if(dfs(0)){
	        printf("%d\n",depth);
	        break;
	    }
	}
}

int main(){
	
    while(~scanf("%d",&n),n){
		IDAstar();
    }
    
    
    return 0;
}