恶性胶质瘤是成人最常见的脑部肿瘤。恶性胶质瘤的致死率为100%,无法治愈,是一种极度的恶性肿瘤。如此糟糕的预后促使研究者及神经外科医生不断学习研究肿瘤生物学,期望创造更好的疗法。
神经外科助理教授Dominique Higgins博士从事肿瘤生物学的研究。他和哥伦比亚大学的研究人员发现,恶性胶质瘤细胞对由饮食中去除特定氨基酸引发的细胞铁死亡(ferrotosis)非常敏感。
“首先,我们在动物模型中发现,饮食中去除特定氨基酸会导致恶性胶质瘤细胞发生铁死亡,” Higgins博士说,“其次,我们发现,去除这些氨基酸提高了诱导肿瘤细胞铁死亡的效率。”
他们的研究成果发表在《Nature Communications》。
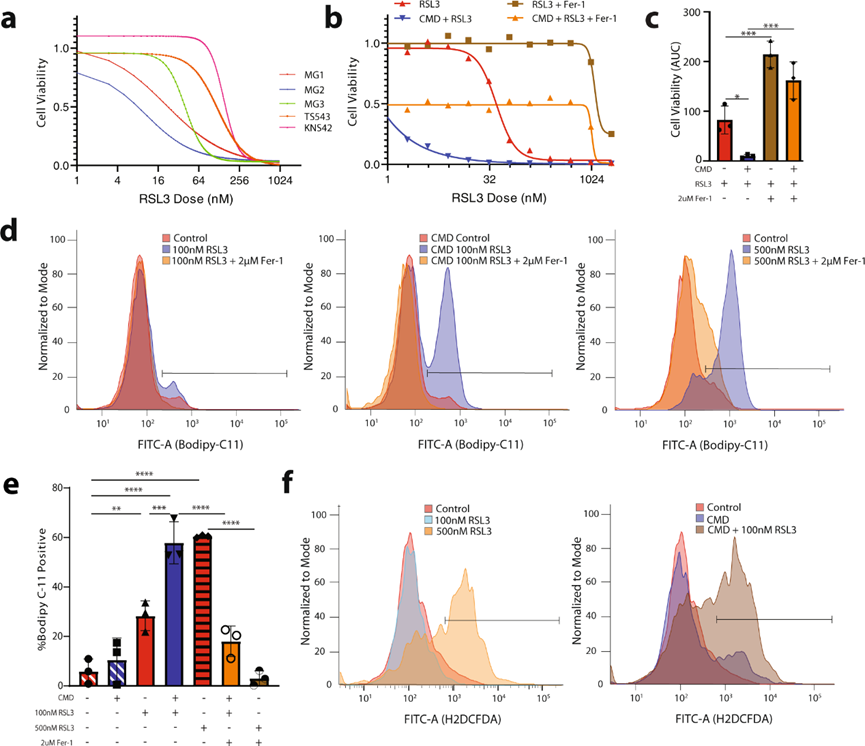
细胞铁死亡是一种依赖于铁的 “细胞程序性死亡”或者是一种导致细胞在命令下“自毁”的生物过程。除非绝对必要,我们的身体不需要杀死细胞,所以这个过程受到某些生物机制的严格控制。十年前细胞铁死亡被公认,研究者们才开始理解这一生物过程。
“近年来对细胞铁死亡的研究发现非常令人兴奋,” 北卡罗来纳大学莱因伯格综合癌症中心的Higgins说,“针对细胞铁死亡的研究越来越多,我们发现它在很多生物过程中发挥着重要作用,不仅仅是在癌症中。”
每个细胞都有一定的安全防护特性,以防止它以一种不可预测的方式经历铁死亡。半胱氨酸和蛋氨酸这两种氨基酸对于阻止细胞发生铁死亡至关重要。我们通常通过饮食摄入这些氨基酸。
因此,Higgins的研究团队决定集中研究这两种成分。
通过定制饮食令动物模型无法摄入半胱氨酸和蛋氨酸,研究者发现神经胶质瘤细胞显著发生了铁死亡。他们还发现,这种饮食会促进化疗药物诱导细胞程序性死亡,这意味着低剂量的化疗药物将会达到更好的效果。最终,定制饮食提高了动物模型的生存率。
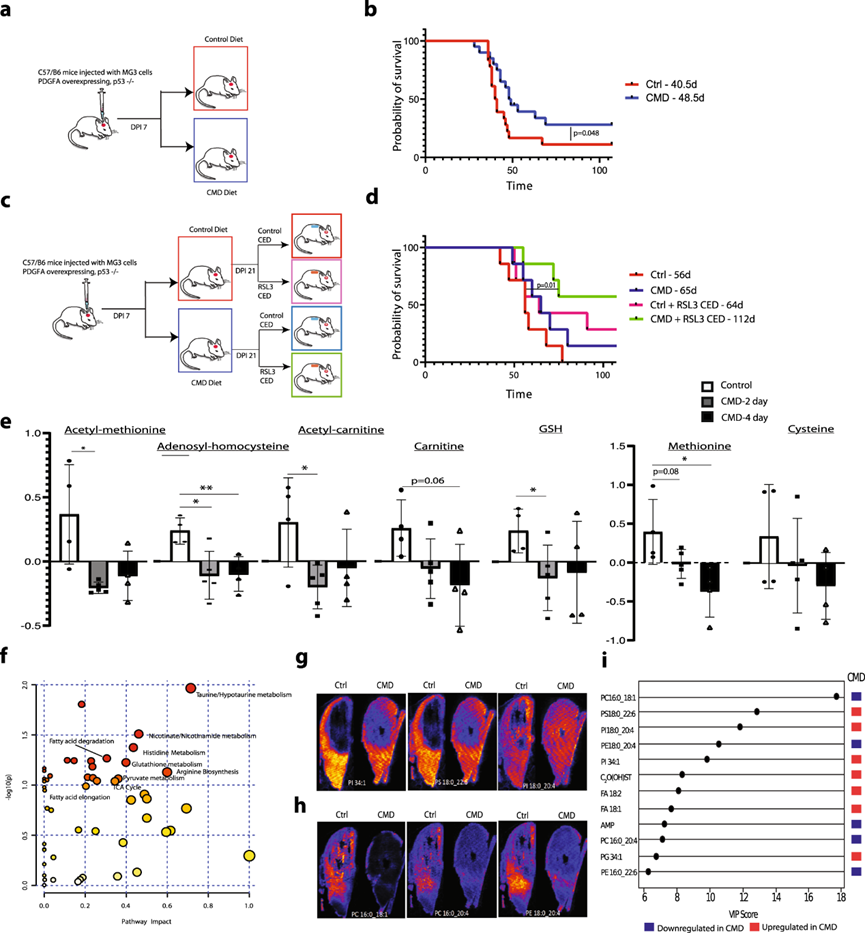
“当前,我们需要找到一种方法:通过饮食既能去除两种成分又能保证患者(尤其是癌症患者)对能量的需求,” Higgins说。
在证明这种饮食在动物模型中是有效的之后,Higgins和他的同事开始研发一项恶性胶质瘤的临床试验。他安排患者在术前定制饮食,以便了解该种饮食是如何影响患者的身体和肿瘤。术后他们会对切除的肿瘤进行分析,研究饮食对肿瘤的影响。
这种类型的饮食也被证明对肉瘤、肺癌和胰腺癌非常有效,因此有希望将这种饮食应用于在化疗和/或切除全身肿瘤后以便为患者提供一些能量。
点击阅读原文:
https://www.sciencedaily.com/releases/2023/04/230407094232.htm
查看原文内容:
https://www.nature.com/articles/s41467-023-36630-w
往期精品(点击图片直达文字对应教程)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
机器学习
后台回复“生信宝典福利第一波”或点击阅读原文获取教程合集