WPF mvvm框架Stylet使用教程-特殊用法

news2025/6/20 16:09:43

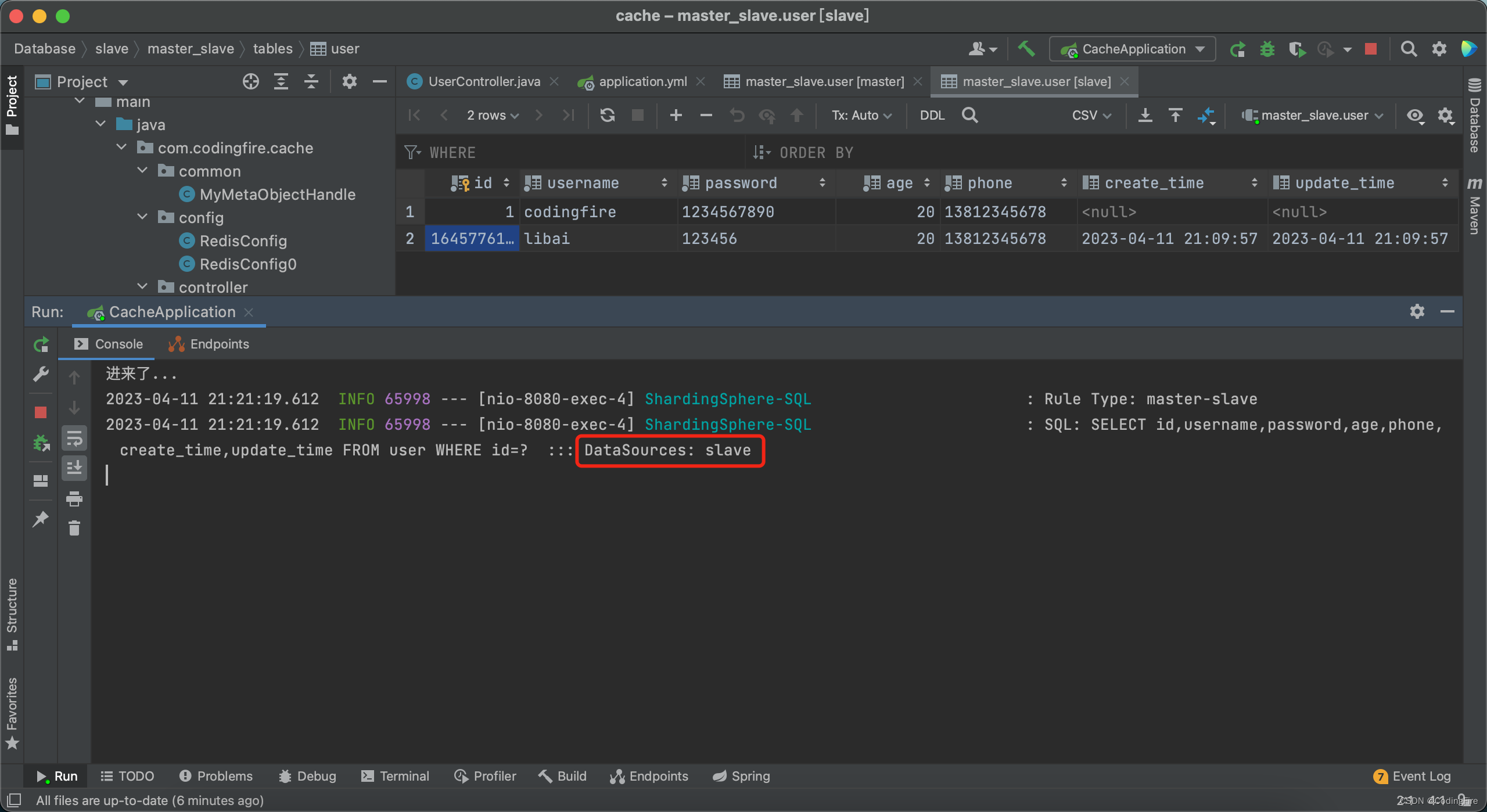
事件绑定

除了绑定Command属性，在WPF中经常需要绑定一些事件的操作，在别的框架中需要引入其他包支持，在Stylet框架中，可以同样使用s:Action进行绑定，对应绑定ViewModel中的方法。

示例：

  XAML:
  <Button
            Width="146"
            Height="41"
            Margin="104,200,0,0"
            HorizontalAlignment="Left"
            VerticalAlignment="Top"
            Content="改名"
            PreviewMouseDown="{s:Action ChangingName}"
            PreviewMouseUp="{s:Action ChangedName}" />
            
   ViewModel：
   
     public void ChangingName()
      {
          ActualName = "改名ing";
      }

      public void ChangedName()
      {
          ActualName = "改名完成";
      }

控制按钮是否启用

只需要增加一个Can+方法名的bool属性，就可以实现控制按钮启用/禁用

例如有一个按钮绑定了方法TestCmd

 <Button
                Width="146"
                Height="41"
                Margin="45,184,0,0"
                HorizontalAlignment="Left"
                VerticalAlignment="Top"
                Command="{s:Action TestCmd}"
                Content="测试2" />

只需要在ViewModel中添加一个属性CanTestCmd

private bool _canTestCmd;
public bool CanTestCmd
{
    get
    {
        return _canTestCmd;
    }
    set
    {
        SetAndNotify(ref _canTestCmd, value);
    }
}

控制CanTestCmd属性，就可以实现，无需将CanTestCmd属性绑定到Button上。

在这里插入图片描述

跨ViewModel进行绑定事件方法

主要是绑定外部的View的控件绑定内部ViewModel的方法，通过s:View.ActionTarget绑定内部ViewModel的属性对象

例如在ShellView中有一个Button，用他来操作子界面view里面的内容，在ShellViewModel中有子界面的VIewModel public UserPageViewModel UserPage { get; private set; },通过 s:View.ActionTarget="{Binding UserPage}"将控件绑定的目标对象改成子界面的ViewModel，然后直接绑定对应事件即可实现

  <Button
            Width="112"
            Height="30"
            Margin="725,80,0,0"
            HorizontalAlignment="Left"
            VerticalAlignment="Top"
            s:View.ActionTarget="{Binding UserPage}"
            Command="{s:Action OutUseTest}"
            Content="修改标题" />
 <ContentControl
            Width="800"
            Height="450"
            Margin="0,188,0,0"
            HorizontalAlignment="Center"
            VerticalAlignment="Top"
            s:View.Model="{Binding UserPage}" />

在UserPageViewModel中的属性和方法

  private string _outText;
  public string OutText
  {
      get
      {
          return _outText;
      }
      set
      {
          SetAndNotify(ref _outText, value);
      }
  }

  public void OutUseTest()
  {
      OutText = "Shell操作修改成功";
  }