目录

计算多元函数的自由极值

计算二元函数在区域D内的最大值和最小值

函数求偏导数的MATLAB命令

例题如下

---

计算多元函数的自由极值

1. 定义多元函数 Z=f(x,x)
2. 求解正规方程fx(x,y)=0,fy(x,y)=0 得到驻点
3. 对于每一个驻点（x0,y0），求二阶偏导 A=  B=  C=
4. 对于每一个驻点(x0,y0)，计算判别式AC-B2。若AC-B2>0，则该驻点是极值点。当A>0为极小值，A<0为极大值；若AC-B2=0，判别式失效，需要进一步判断。若AC-B2<0，则该驻点不是极值点。

计算二元函数在区域D内的最大值和最小值

设函数Z=f(x,y)在有界区域D上连续，则f(x,y)在D上必定有最大值和最小值。

求f(x,y)在D上的最大值和最小值的一般步骤为：

1. 计算f(x,y)在D内所有驻点处的函数值、
2. 计算f(x,y)在D的各个边界上的最大值和最小值
3. 将上述函数值进行比较，最终确定出在D内的最大值和最小值

函数求偏导数的MATLAB命令

MATLAB中主要用diff求函数的偏导数

例题如下

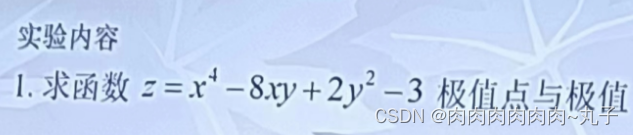
clear;close;
x=linspace(-5,5,300);
y=x;
[X,Y]=meshgrid(x,y);
Z=X.^4-8*X.*Y+2*Y.^2-3;
mesh(X,Y,Z)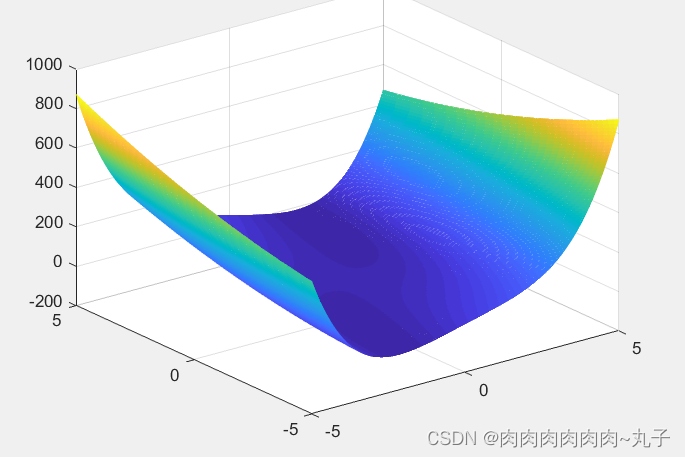

clear;close;
x=-1:0.1:1;
y=-1:0.1:1;
[X,Y]=meshgrid(x,y);
Z=X.^2-Y.^2;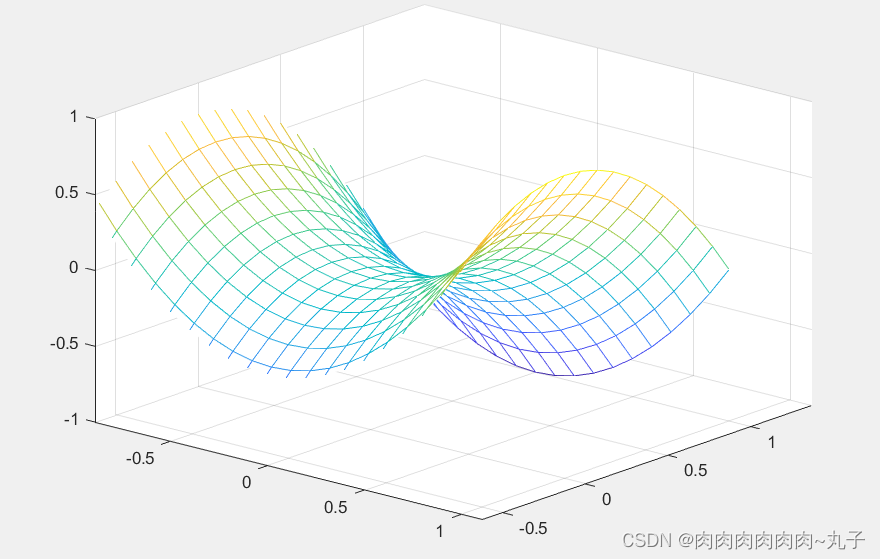

clear;close;
[x,y]=meshgrid([-2:0.05:2],-2:0.05:2);
z1=x.^2-2*y^2;
z2=2*x-3*y;
mesh(x,y,z1);
hold on;
mesh(x,y,z2);
r=(abs(z1-z2)<=0.07);
zz=r.*z1;
yy=r.*y;
xx=r.*x;
plot(xx(r~=0),yy(r~=0),zz(r~=0),'.')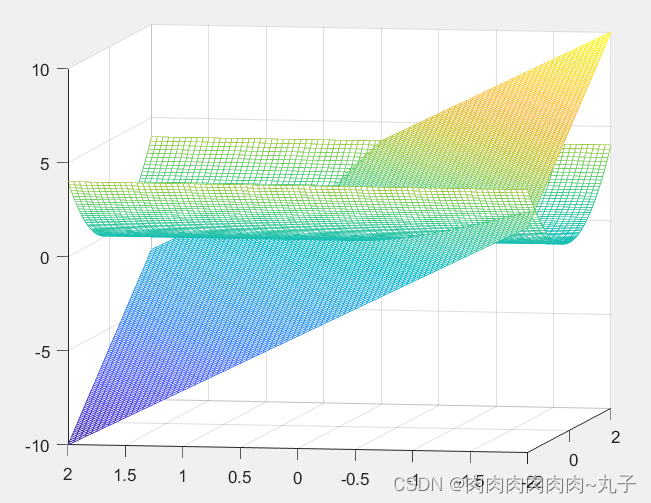

 

 

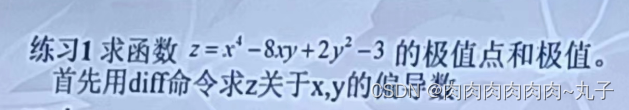
syms x y
x=linspace(-10,10,100);
y=x;
[X,Y]=meshgrid(x,y);
Z=X.^4+Y.^4-4*X.*Y+1;
contour(X,Y,Z,6000)