【算法】01-算法解剖学-二分查找

news2025/6/20 15:55:14

汝之观览，吾之幸也！本系列主要讲解的是算法知识，从算法基本概念，利用图解的方式更好的认识算法，再通过letcode算法题
进行进一步的巩固。刷题三步走（1、掌握一门基本的编程语言；2、深入理解基础的数据结构；3、按照特定模块进行系统性刷题）

一、定义

二分查找是一种算法，其输入是一个有序的元素列表。如果要查找的元素包含在列表中，二分查找返回其位置索引；否则返回-1。

二、数据结构

一个有序的元素列表

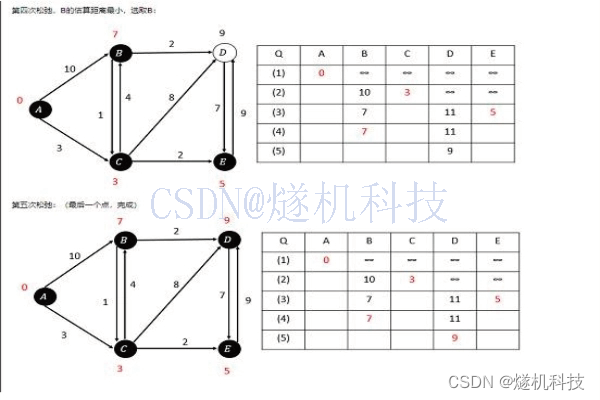
三、算法图解

如果想从1~24000个数字中查找到一个数字，需要多少步？
按照从1开始的话，那么可能需要24000次，但是使用二分查询最多需要 $log_2^{24000}$ =18步。这就是二分查询的好处。
在这里插入图片描述
对数是幂运算的逆运算

大O表示法是一种特殊的表示法，指出了算法的速度有多快。
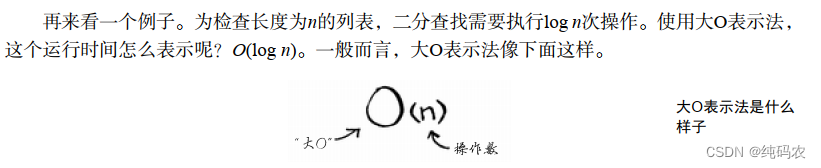
在这里插入图片描述

不同的算法所展示的时间长度
在这里插入图片描述

四、Java实例

可参考Java jdk中的Arrays.binarySearch方法

int[] a = new int[100];
for (int i = 0; i < a.length; i++) {
    a[i] = i + 1;
}
int key=45;
// 调用Arrays工具类二分查找方法
Arrays.binarySearch(a,key);

五、LetCode中的二分查找

题目数：704. 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例：

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

解题思路：

1、初始化左边与右边的索引值,设置left=0,right=nums.length-1
2、判断当前左边与右边的索引值大小,循环判断 left<= right
3、 获取target中间值的位置,根据中间值的索引值得到对应的值
4、判断中间值与target比较
4.1、如果target>midValue，表示target在中间值的右边，则需要更改左边的索引值
4.2、如果target<midValue，表示target在中间值的左边，则需要更改右边的索引值
4.3、只有target=midValue，输出得到的索引值
5、如果left > right，返回-1

public int search(int[] nums, int target) {
    // 初始化左边与右边的索引值
    int leftIndex = 0;
    int rightIndex = nums.length-1;
    // 判断当前左边与右边的索引值大小
    while(leftIndex <= rightIndex){
        // 获取target中间值的位置
        int midIndex = (leftIndex+rightIndex)>>>1;
        // 根据中间值的索引值得到对应的值
        int midValue= nums[midIndex];
        // 判断中间值与target比较
        if(target>midValue){
            // 如果target>midValue，表示target在中间值的右边，则需要更改左边的索引值
            leftIndex = midIndex+1;
        }else if(target<midValue){
            // 如果target<midValue，表示target在中间值的左边，则需要更改右边的索引值
            rightIndex= midIndex-1;
        }else{
            // 只有target=midValue，输出得到的索引值
            return  midIndex;
        }
    }
    return  -1;
}