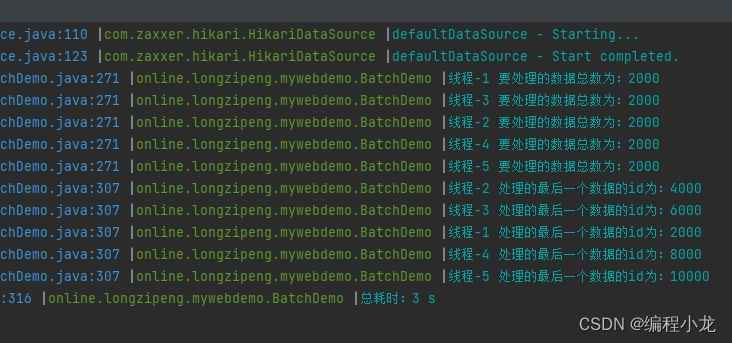
通过在线学习提供边缘推理服务

一、论文研究背景、动机和主要贡献

研究背景

趋势：机器学习模型训练从中央云服务器逐步转移到边缘服务器

好处：

• 与云相比：a.低延迟 b.保护用户隐私（数据不会上传到云）
• 与on-device相比：克服设备电量、资源限制

研究动机

挑战：

• 边缘推理需要对跨网络的机器学习模型进行管理
• 云->边缘涉及准确性和资源消耗之间的权衡；且涉及决策耦合：当前所做的任何决策都有可能限制下一步所做的决策（资源需求是在线变化的）
• 推断任务的到达是不可预测的，如何清除任务推断队列是具有挑战性的

主要贡献

研究了在异构、资源受限的分布式边缘基础设施上在线优化机器学习服务的整体推理精度问题，同时适应不可预测的推理工作量。

• 将问题建模为一个带有长期约束的时变非线性整数规划：
  $$整数规划\{\begin{array}{l}问题目标：最大化整体推理精度\\ 问题约束\{\begin{array}{l}队列状态转换\\ 机器学习模型选择和交付\\ 推理工作负载分布\end{array}\end{array}$$
  决策存在滞后性：只有决策了，才知道是否满足约束。

  方案：选择设计在线算法，优化目标和上限累积，长期约束违反随时间的推移。

• 我们设计了多项式时间在线算法

  该算法由一个在线学习组件和一个随机舍入组件组成，该组件在每个时隙中进行分数阶决策，而不观察当前输入，并将分数阶决策转换为整数，而不改变期望中的约束违反。

  • 在线学习组件：凸凹等效公式，采用以前的输入而非当前的输入。
  • 随机舍入组件：将分数决策舍入为整数，同时让两个分数相互补偿，并保持随机整数的期望等于相应的分数。

• 性能：只会对最优性损失产生次线性动态遗憾，而对长期约束违反则会产生次线性动态拟合【两个指标】

二、系统模型和问题公式化

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sgHL920J-1678173510342)(%E9%80%9A%E8%BF%87%E5%9C%A8%E7%BA%BF%E5%AD%A6%E4%B9%A0%E6%8F%90%E4%BE%9B%E8%BE%B9%E7%BC%98%E6%8E%A8%E7%90%86%E6%9C%8D%E5%8A%A1.assets/image-20230305131629138.png)]

系统模型

边缘计算设备：一系列分布式异构边缘 N = { 1 , 2 , . . . , N } \mathcal{N}=\{1,2,...,N\} N={1,2,...,N}，使用$c_n$表示边缘的容量。

机器学习模型：M个机器学期模型 M = { 1 , 2 , . . . , M } \mathcal{M}=\{1,2,...,M\} M={1,2,...,M}，预训练并存储在云中。

• 模型m在t时刻的精度损失：$a_{m,t}$
• 模型资源需求：$d_m$
• 模型大小：$s_m$
• 模型m的推理能力：$p_m$

推断工作负荷处理：

• 用户在t时刻提交到边缘N的推断数量：$r_{n,t}$
• 先进先出队列长度：$q_{n,t}$
• 迁移代价：$b_{n,t}$

控制变量：

• 在t时刻，边缘n是否拥有模型m： z n , m , t = { 1 , 0 } z_{n,m,t}=\{1,0\} zn,m,t​={1,0}
• 在t时刻，边缘n上驻留的模型m的实例数量：$x_{n,m,t}$
• 在t时刻，从边缘n迁移到边缘n’的用户查询数量：$y_{n,n^{\prime },t}$

问题公式化

问题目标：最小化整体的精度损失
$$\sum _{t=1}^T\sum _n\sum _m{a}_{m,t}{x}_{n,m,t}$$
问题约束：

• 队列状态转换，保证队列长度非负
  $$\begin{gathered} \forall t,n:q_{n,t+1}=[q_{n,t}+\sum _{n^{\prime }}{y}_{n^{\prime },n,t}-\sum _m{p}_m{x}_{n,m,t}{]}^{+} \\ {q}_{n,1}\ge 0,q_{n,T+1}=0 \end{gathered}$$

• 推理工作负载分布
  $$\forall t,n:\sum _{n^{\prime }}{y}_{n,n^{\prime },t}=r_{n,t}$$

• 迁移代价
  $$\forall t,n:\sum _m{s}_m[z_{n,m,t}-z_{n,m,t-1}{]}^{+}+\tau \sum _{n^{\prime },n^{\prime }\ne n}(y_{n,n^{\prime },t}+y_{n^{\prime },n,t})\le b_{n,t}$$
  下载模型+创建新的模型实例

• 确保只有当模型决定驻留在边缘时，边缘才能有模型的实例
  $$\forall t,n,m:d_m{x}_{n,m,t}\le z_{n,m,t}{c}_n$$

• 确保用于处理推理查询的资源处于边缘容量之内
  $$\forall t,n:\sum _m{d}_m{x}_{n,m,t}\le c_n$$

• 变量为整数
  ∀ t , n , n ′ , m : x n , m , t , y n , n ′ , t ∈ N , z n , m , t ∈ { 0 , 1 } \forall t,n,n',m:x_{n,m,t},y_{n,n',t}\in \N,z_{n,m,t}\in\{0,1\} ∀t,n,n′,m:xn,m,t​,yn,n′,t​∈N,zn,m,t​∈{0,1}

问题公式化：

问题：没有用户推理查询的先验知识，否则在知道这样的工作量之前，可在每个时间段动态地做出决策，同时仍然满足每个时间段的约束;

解决方式：选择只在长期内强制约束，并设计在线算法使目标最小化，并约束累积约束违反随时间的变化。
min ⁡ ∑ t = 1 T { ∑ n ∑ m a m , t x n , m , t }  s.t.  ∀ n : ∑ t = 1 T g t 0 , n ≤ 0 , ∀ n : ∑ t = 1 T g t 1 , n : = ∑ t = 1 T { ∑ n ′ y n , n ′ , t − r n , t } ≤ 0 , ∀ n : ∑ t = 1 T g t 2 , n : = ∑ t = 1 T { r n , t − ∑ n ′ y n , n ′ , t } ≤ 0 , ∀ n : ∑ t = 1 T g t 3 , n ≤ 0 , ∀ n , m : ∑ t = 1 T g t 4 , n , m ≤ 0 , ∀ t , n : h t n : = ∑ m d m x n , m , t − c n ≤ 0 ,  var.  ∀ t , n , m : x n , m , t , y n , n ′ , t ∈ N , z n , m , t l o a d ∈ { 0 , 1 } , \begin{aligned} \min & \sum_{t=1}^T\left\{\sum_n \sum_m a_{m, t} x_{n, m, t}\right\} \\ \text { s.t. } & \forall n: \sum_{t=1}^T g_t^{0, n} \leq 0, \\ & \forall n: \sum_{t=1}^T g_t^{1, n}:=\sum_{t=1}^T\left\{\sum_{n^{\prime}} y_{n, n^{\prime}, t}-r_{n, t}\right\} \leq 0, \\ & \forall n: \sum_{t=1}^T g_t^{2, n}:=\sum_{t=1}^T\left\{r_{n, t}-\sum_{n^{\prime}} y_{n, n^{\prime}, t}\right\} \leq 0, \\ & \forall n: \sum_{t=1}^T g_t^{3, n} \leq 0, \\ & \forall n, m: \sum_{t=1}^T g_t^{4, n, m} \leq 0, \\ & \forall t, n: h_t^n:=\sum_m d_m x_{n, m, t}-c_n \leq 0, \\ \text { var. } & \forall t, n, m: x_{n, m, t}, y_{n, n^{\prime}, t} \in \mathbb{N}, z_{n, m, t}^{l o a d} \in\{0,1\}, \end{aligned} min s.t.  var. ​t=1∑T​{n∑​m∑​am,t​xn,m,t​}∀n:t=1∑T​gt0,n​≤0,∀n:t=1∑T​gt1,n​:=t=1∑T​{n′∑​yn,n′,t​−rn,t​}≤0,∀n:t=1∑T​gt2,n​:=t=1∑T​{rn,t​−n′∑​yn,n′,t​}≤0,∀n:t=1∑T​gt3,n​≤0,∀n,m:t=1∑T​gt4,n,m​≤0,∀t,n:htn​:=m∑​dm​xn,m,t​−cn​≤0,∀t,n,m:xn,m,t​,yn,n′,t​∈N,zn,m,tload​∈{0,1},​
约束转换为长期版本，并予以简化处理：

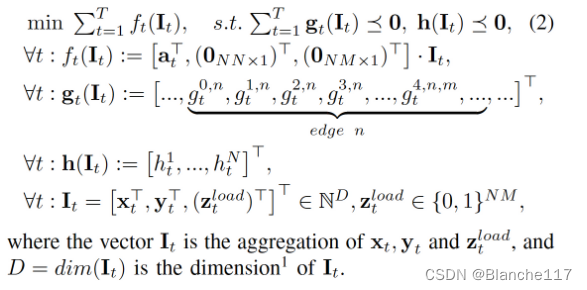
$I_t$是x,y,z组成的矩阵。

三、在线算法设计

在线学习：每一个时隙的决策应该从刚刚过去的决策中学习。

设计了一种新型的边缘推理多项式时间在线算法(OAEI)，它有两个组成部分：

• 在线学习组件：克服对不确定用户查询的遗忘，并根据先前的观察输入结果返回部分决策
• 随机舍入组件：将分数决策转换为整数决策

在线算法组件

设计了一种交替的原对偶方法。注意到，求解的凸问题：

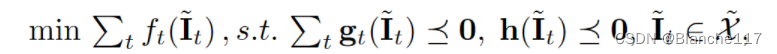
等价于求解：

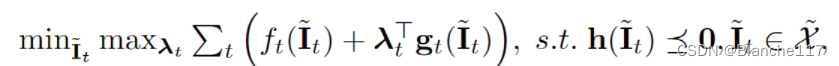
那么Lagrange函数为：

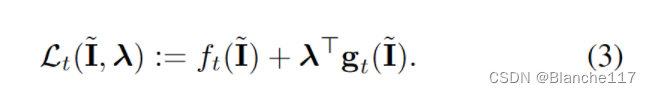
因此，我们可以在通过修改的下降步骤使${\mathcal{L}}_t(I，{\lambda }_{t+1})$相对于原始变量I最小化和通过双上升步骤使${\mathcal{L}}_t(It，\lambda )$相对于拉格朗日乘子$\lambda$最大化之间进行交替。具体来说，在时刻$t+1$，解决了以下问题：

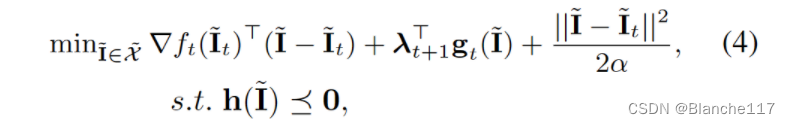
为了将分数决策$I_t,t$转换为整数，提出了一个随机舍入组件作为算法2。

该方式是基于primal dual的，是不是可以理解成等价为内点法创建的另一种创新的、适用于本问题的一种解法

随机舍入组件

随机舍入组件这里只关注01整型变量$z_{n,m,t}$如何处理的。

Step1：分别处理每个小数值，并将其舍入为整数，其期望是舍入后的小数值本身，如第1行到第5行所示。

其实对于0~1之间的数而言，上述的操作及相当于根据数据接近1的程度对其取1或0

更具体地说，分数值可以分为两部分：小数部分$\lfloor A_t\rfloor$和实部分$A_t$。小数作四舍五入的概率。