CCF CSP认证2022年6月归一化处理、寻宝！大冒险！、光线追踪

这是我第一次参加了这次CSP考试，300分，写了124三题，模拟题到现在都没看过题面没看，笑，t4写成模拟加数据结构，200+行，因为一个小错误调了1h，错失了大好机会。考试环境的VSC配置的字体太小，甚至连空格都看不清有还是没有，当时没想到可以重新配置，这可能也是我t4调了1h的原因。

距离下一次CSP考试考试还有20天左右，特此回顾。代码均为考试时提交的代码，补充思路。

T1 归一化处理

思路

数据归一化处理，根据给定公式进行计算。

在这里插入图片描述

这里要求了输出精度，通过流的格式标志值 $ios\_base::fixed$ 和 $s e t p r e c i s i o n ()$ 设置输出小数点后10位。

cout << fixed << setprecision(10) << (a[i] - av) / sD << '\n';

代码

void solve() {
    int n; cin >> n;

    vector<double> a(n);
    double sum = 0;
    for (int i = 0; i < n; i++) cin >> a[i], sum += a[i];
    double av = sum / n;

    double sD = 0;
    for (int i = 0; i < n; i++) {
        sD += (a[i] - av) * (a[i] - av);
    }
    sD /= n;
    sD = sqrt(sD);

    for (int i = 0; i < n; i++) {
        cout << fixed << setprecision(10) << (a[i] - av) / sD << '\n';
    }
}

T2 寻宝！大冒险！

思路

在这里插入图片描述
给定一个大矩阵 $L$ 和小矩阵 $S$ ，均为01矩阵，问 $L$ 有多少处和 $S$ 匹配（ $L$ 有多少个子矩阵和 $S$ 相等）。
暴力匹配，时间为 $O(L^2S^2)$ ，虽然一旦不匹配就可以终止，但乐观估计不优于 $O(L^2)$ .
因此，需要采取一些方法，注意到 $n\leq 1000$ ，即‘1’的个数不超过1000，而且
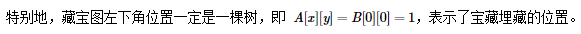
在这里插入图片描述
因此从大矩阵‘1’的位置开始匹配，理论复杂度为 $O(n\times S^2)$ ，约为 $2.5 e 6$ ，时间上可以过，但是还有空间的问题，无法开 $1 e 18$ 的 $b o o l$ 数组，因此用 $s e t < p a i r < i n t, i n t > >$ 仅存储‘1’的坐标，匹配时要调用 $f i n d ()$ 方法找大矩阵中的对应位置，牺牲时间换空间，因此最终时间为 $O(nlogn\times S^2)$ ，约为 $2.5 e 7$ .

代码

set<pair<int, int> > Set;
vector<pair<int, int> > a, b;

void solve() {
    int n, L, S;
    cin >> n >> L >> S;

    int x, y;
    for (int i = 1; i <= n; i++) {
        cin >> x >> y;
        Set.insert({x, y});
    }

    int m;
    for (int i = 0; i <= S; i++) {
        for (int j = 0; j <= S; j++) {
            cin >> m;
            if (m) {
                a.push_back({S - i, j});    // a tree
            }
            else b.push_back({S - i, j});
        }
    }
    int ans = 0;
    for (auto i : Set) {

        if (i.first + S > L || i.second + S > L) continue;
        bool ok = 1;
        // cout << "i: " << i.first << ' ' << i.second << '\n';
        for (auto j : a) {
            // cout << "j: " << j.first << ' ' << j.second << '\n';
            int tx = i.first + j.first;
            int ty = i.second + j.second;
            // cout << tx << ' ' << ty << '\n';
            if (Set.find({tx, ty}) == Set.end()) {
                ok = 0;
                break;
            }
        }

        for (auto j : b) {
            if (!ok) break;
            int tx = i.first + j.first;
            int ty = i.second + j.second;
            // cout << tx << ' ' << ty << '\n';
            if (Set.find({tx, ty}) != Set.end()) {
                ok = 0;
                break;
            }
        }
        if (ok) ans++;
    }

    cout << ans << '\n';
}

T4 光线追踪

思路

原来这题是图形学的背景，这学期刚刚在学CG，确实CG中很多用数据结构优化（比如多边形填充的APT）的算法。
在这里插入图片描述
限制了光线只能水平或者竖直地射，包括反射后的光线，而反射面的端点坐标均为整数，光源也设置在整点位置，因此可以认为光线在网格格线上运动，更进一步，可以认为反射面只设定在格点上。

光线在反射过程中存在耗散。
在这里插入图片描述
1，2定义了反射面的增删操作，3设置光源询问 $t$ 时间后，光线的位置 $(x, y)$ ，以及剩余光线强度 $I$ 。

这个 $3 e 5$ 的保证意味着可以 $O (n)$ 地将反射面的性质（耗散率，放置方向）存储（或者移除）到一定区间的格点中，用格点代表反射面，格点数就是 $\sum|x_1-x_2|$ .
在这里插入图片描述
网格大小为 $1e9^2$ ，因此必须不能 $O (t)$ 模拟光线的运动。光线的运动状态通过当前位置 $(x, y)$ 和方向 $d$ ，如果 $d$ 不变，可以 $O (1)$ 确定 $t$ 时间后的位置，而 $d$ 变化由反射引起，反射是由于经过了反射面，即具有反射性质的格点（下称为格点）。

如何快速找到该点？ $s e t$ 上二分，将反射点存储于 $s e t$ 中，从当前点 $(x, y)$ 出发找第一个反射点。
通过 $m a p < l l, s e t < l l > >$ 嵌套STL存储，分别存储X，Y方向每条线上的反射点，其实一开始，我用了 $s e t < i n t > s e t X [2 * N]$ ，提交后RE了，因为坐标可能为负数，而下标不能为负，然后第一次想到了这种用法，将数组下标范围扩大至负数域，而且是动态地开辟空间，不用为内存限制而烦恼！

结合代码讲讲：
定义了结构体 $m i r r o r$ ，解决题目规定的对反射面整体的增加和删除操作，对应结构体方法 $i n i t$ 和 $c l r$ ，而 $r e s e t$ 是将反射性质赋予区域中的格点，就是将该点存储于 $m a p < l l, s e t < l l > >$ ， $c l r$ 中实现了移除，下面这句是进行空间的回收，动态性！其实这里可以将 $i n i t$ 和 $r e s e t$ 合在一起写。

if (setX[x].size() == 0) setX.erase(x);

$w o r k$ 函数模拟光线的运动，是递归函数，输入参数 $x, y$ 是当前坐标， $d$ 是方向， $I$ 是强度， $t$ 是询问 $t$ 时刻后的位置。

void work(ll x, ll y, int d, double I, ll t) {

这个函数我按照运动方向分为了4个部分写，因为每个方向上 $s e t$ 调用的二分方法不同， $upper\_bound$ 或者 $lower\_bound$ ，而且边界情况也不好统一表达，只能 $i f e l s e$ 分类讨论了。
具体看一种情况，光线沿着 $x$ 轴增加：
此时 $y$ 不变，首先判断该格线上是否有反射点，没有访问会RE：

if (setY.find(y) == setY.end()) {

若没有，则一直前进；否则，则调用 $s e t$ 自带的二分方法：

auto it = setY[y].upper_bound(x);   // 找到第一个大于x的数

若没有找到这样的反射点，则一直前进；否则可能发生发射，还要检查到达该点的用时，时间充足发生反射，写到这里大家肯定发现这是道具有大模拟性质的t4了。
发生反射，由于光线原来方向沿 $x$ 增加，只可能变为沿 $y$ 方向增加或者减少，这个通过镜子的放置方向确定，递归。

代码

#include<bits/stdc++.h>
using namespace std;
using ll = long long;

const int N = 1e5 + 5;
const int maxn = 1e5 + 5;

// set<int> setX[2 * N];
// set<int> setY[2 * N];

map<ll, set<ll> > setX;
map<ll, set<ll> > setY;
map<pair<ll, ll>, int> mp;

struct  mirror
{
    void init(int ID, ll a1, ll b1, ll a2, ll b2, double A) {
        id = ID;
        x1 = a1; y1 = b1; x2 = a2; y2 = b2; a = A;
    }
    void reset() {
        if (x1 > x2) dx = -1;
        else dx = 1;
        if (y1 > y2) dy = -1;
        else dy = 1;

        ll x = x1 + dx, y = y1 + dy;
        while (x != x2) {
            setX[x].insert(y);
            setY[y].insert(x);
            mp[{x, y}] = id;    // 将点对应至镜子
            x += dx; y += dy;
        }
    }
    void clr() {
        ll x = x1 + dx, y = y1 + dy;
        while (x != x2) {
            setX[x].erase(y);
            setY[y].erase(x);
            if (setX[x].size() == 0) setX.erase(x);
            if (setY[y].size() == 0) setY.erase(y);
            mp.erase({x, y});
            x += dx; y += dy;
        }
    }
    int id;
    ll x1, y1, x2, y2;
    int dx, dy;
    double a;
} M[maxn];

void work(ll x, ll y, int d, double I, ll t) {
    // cout << "work: " << x << ' ' << y << ' ' << d << ' ' << I << ' ' << t << '\n';
    
    if (I < 1.0) {  // 已经完全耗散
        cout << "0 0 0\n";
        return;
    }
    // if (x < 0 || y < 0) return;
    if  (d == 0) {  // x -> 沿着x轴增加
        if (setY.find(y) == setY.end()) {
            cout << x + t << ' ' << y << ' ' << (int)I << '\n';
            return;
        }
        auto it = setY[y].upper_bound(x);   // 找到第一个大于x的数
        if (it == setY[y].end()) {  // 若无则代表没有镜子
            cout << x + t << ' ' << y << ' ' << (int)I << '\n';
            return;
        }
        else {
            ll nx = *it;
            if (t < nx - x) {  // 看剩余时间是否充足
                cout << x + t << ' ' << y << ' ' << (int)I << '\n';
                return;
            }
            int mir = mp[{nx, y}];  // 进行一次反射
            auto Mir = M[mir];
            if (Mir.dx * Mir.dy > 0) {  // 判断镜子方向
                work(nx, y, 1, I * Mir.a, t - (nx - x));
            }
            else {
                work(nx, y, 3, I * Mir.a, t - (nx - x));
            }
        }
    }
    else if (d == 1) {  // y ^
        if (setX.find(x) == setX.end()) {
            cout << x << ' ' << y + t << ' ' << (int)I << '\n';
            return;
        }
        auto it = setX[x].upper_bound(y);
        if (it == setX[x].end()) {
            cout << x << ' ' << y + t << ' ' << (int)I << '\n';
            return;
        }
        else {
            ll ny = *it;
            if (t < ny - y) {
                cout << x << ' ' << y + t << ' ' << (int)I << '\n';
                return;
            }
            int mir = mp[{x, ny}];
            auto Mir = M[mir];
            if (Mir.dx * Mir.dy > 0) {
                work(x, ny, 0, I * Mir.a, t - (ny - y));
            }
            else {
                work(x, ny, 2, I * Mir.a, t - (ny - y));
            }
        }
    }
    else if (d == 2) {  // x <- 沿着x轴减少
        if (setY.find(y) == setY.end()) {
            cout << x - t << ' ' << y << ' ' << (int)I << '\n';
            return;
        }
        auto it = setY[y].lower_bound(x);
        if (it == setY[y].begin()) {    // 没有小于x的数
                cout << x - t << ' ' << y << ' ' << (int)I << '\n';
                return;
        }
        else {
            it--;   // 第一个小于x的数
            ll nx = *it;
            if (t < x - nx) {
                cout << x - t << ' ' << y << ' ' << (int)I << '\n';
                return;
            }
            int mir = mp[{nx, y}];
            auto Mir = M[mir];
            if (Mir.dx * Mir.dy > 0) {
                work(nx, y, 3, I * Mir.a, t - (x - nx));
            }
            else {
                work(nx, y, 1, I * Mir.a, t - (x - nx));
            }
        }
    }
    else if (d == 3) {  // y v
        if (setX.find(x) == setX.end()) {
            cout << x << ' ' << y - t << ' ' << (int)I << '\n';
            return;
        }
       auto it = setX[x].lower_bound(y);
        if (it == setX[x].begin()) {
                cout << x << ' ' << y - t << ' ' << (int)I << '\n';
                return;
        }
        else {
            it--; 
            ll ny = *it;
            if (t < y - ny) {
                cout << x << ' ' << y - t << ' ' << (int)I << '\n';
                return;
            }
            int mir = mp[{x, ny}];
            auto Mir = M[mir];
            if (Mir.dx * Mir.dy > 0) {
                work(x, ny, 2, I * Mir.a, t - (y - ny));
            }
            else {
                work(x, ny, 0, I * Mir.a, t - (y - ny));
            }
        }
    }
}

void solve() {
    int m; cin >> m;

    ll op, x1, y1, x2, y2, d, t, k;
    double a, I;
    for (int i = 1; i <= m; i++) {
        cin >> op;

        if (op == 1) {
            cin >> x1 >> y1 >> x2 >> y2 >> a;
            M[i].init(i, x1, y1, x2, y2, a);    // 添加反射镜
            M[i].reset();
        }
        else if (op == 2) {
            cin >> k;
            M[k].clr();
        }
        else if (op == 3) {
            cin >> x1 >> y1 >> d >> I >> t;
            if (t == 0) {
                cout << x1 << ' ' << y1 << ' ' << (int)I << '\n';
            }
            work(x1, y1, d, I, t);
        }
    }
}

int main() {
    // freopen("e.in", "r", stdin);
    // long double tt = 1.0;
    // cout << (int)tt << '\n';

    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    solve();
    // cout << "Hello!\n";

    return 0;
}