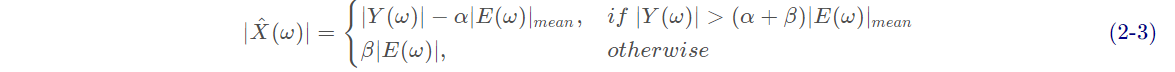目录
3.5.1伪随机函数的非正式定义
|Func_n| 有多大?
DEFINITION 3.24 伪随机函数的正式定义
Example 3.25 一个不安全的反例
3.5.1伪随机函数的非正式定义
伪随机函数(PRFs)推广了伪随机发生器的概念。
F : {0, 1}∗× {0, 1}∗→ {0, 1}∗
F有两个输入,k和x,即F(k,x)
如果有一个多项式时间算法可以计算F,我们就称F为高效的
安全参数n规定了密钥k的长度、输入长度和输出长度。
对于任意的k
![]()
函数F的输入被定义为
![]()
在这种情况下,
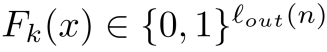
除非另有说明,为了简单起见,我们假设F是保留长度的,即
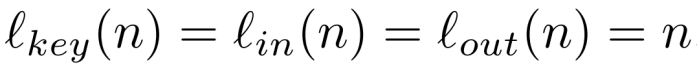
我们还有如下定义
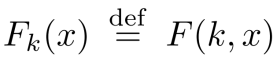
设Func_n表示映射n位字符串到n位字符串的所有函数的集合。
从与Fk(x)具有相同定义域和值域的集合Func_n中随机均匀挑选出来的一个函数,如果函数Fk(x)(其中k是随机均匀选择的),和这个被挑选出来的函数是不可区分的,那我们就称F具有伪随机性。换句话说,不存在PPT敌手能够区分其正在交互的对象是一个Func_n中的真随机函数,还是伪随机函数F
|Func_n| 有多大?
我们可以将任何一个在有限域上函数f视为一个大的查找表,它将f(x)存储在用x标记的表的行中,
以n=2为例,我们取一个f∈Func_2,f可表示为
| x1=00 | f(x1) |
| x2=01 | f(x2) |
| x3=10 | f(x3) |
| x4=11 | f(x4) |
每个f(xi)都是长度为n的字符串,一共2^n行
把所有的f(xi)合成一行,合成一个长度为n*(2^n)的字符串
f是在Func_n中任取的,Func_n的大小正是所有长度为n*(2^n)的字符串的数量
最终我们得到
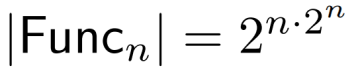
DEFINITION 3.24 伪随机函数的正式定义
一个高效的、长度保留的、含有参数k的函数F: {0,1}∗×{0,1}∗→{0,1}∗,如果对于所有的PPT区分器D,有一个可忽略函数negl使得
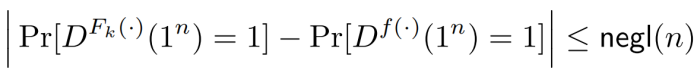
那么我们称F是一个伪随机函数
其中区分器D是不知道密钥k的。如果给定了k,那么区分Fk的预言机和f的预言机是轻而易举的
k如果是被D已知的,相当于Fk是确定性的。这意味着,如果k被揭示出来,任何关于伪随机性的说法都不再成立
Example 3.25 一个不安全的反例
假设F(k, x) = k⊕x。当k时随机均匀选择时,对于任何输入x,Fk(x)的值都是均匀分布的。然而,F不是伪随机的,因为它在任何两点上的值都是相关的。考虑区分器D采取这样的策略:它在不同的点x1,x2上询问其预言机O以获得值y1 = O(x1)和y2 = O(x2),当且仅当y1⊕y2 = x1⊕x2时输出1。
当O=Fk时,y1⊕y2 =k⊕x1⊕k⊕x2= x1⊕x2,此时D输出1的概率为1
当O=f∈Func_n时
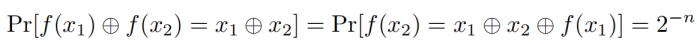
显然1-2^(-n)并不是可忽略的,所以 F 不是伪随机函数