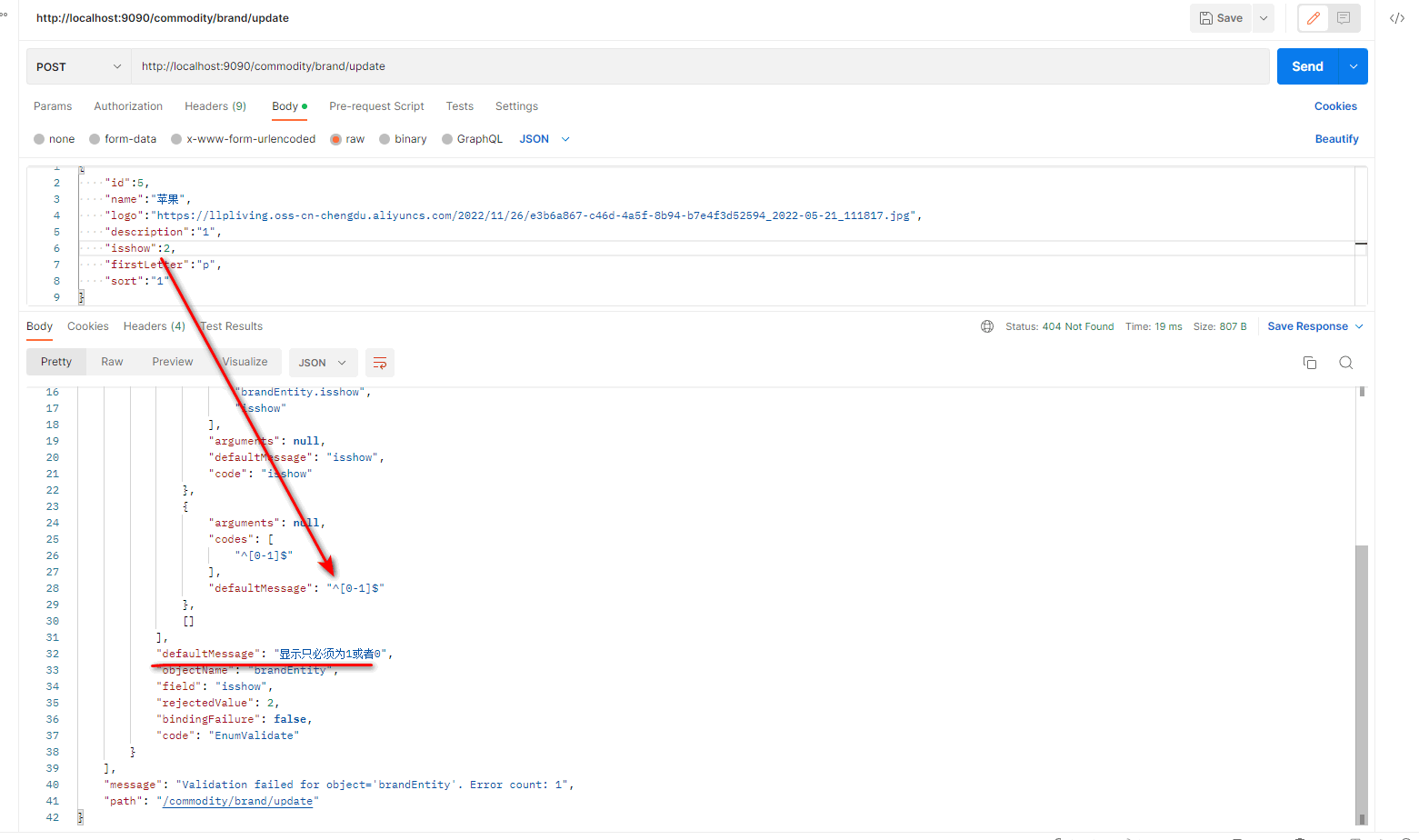
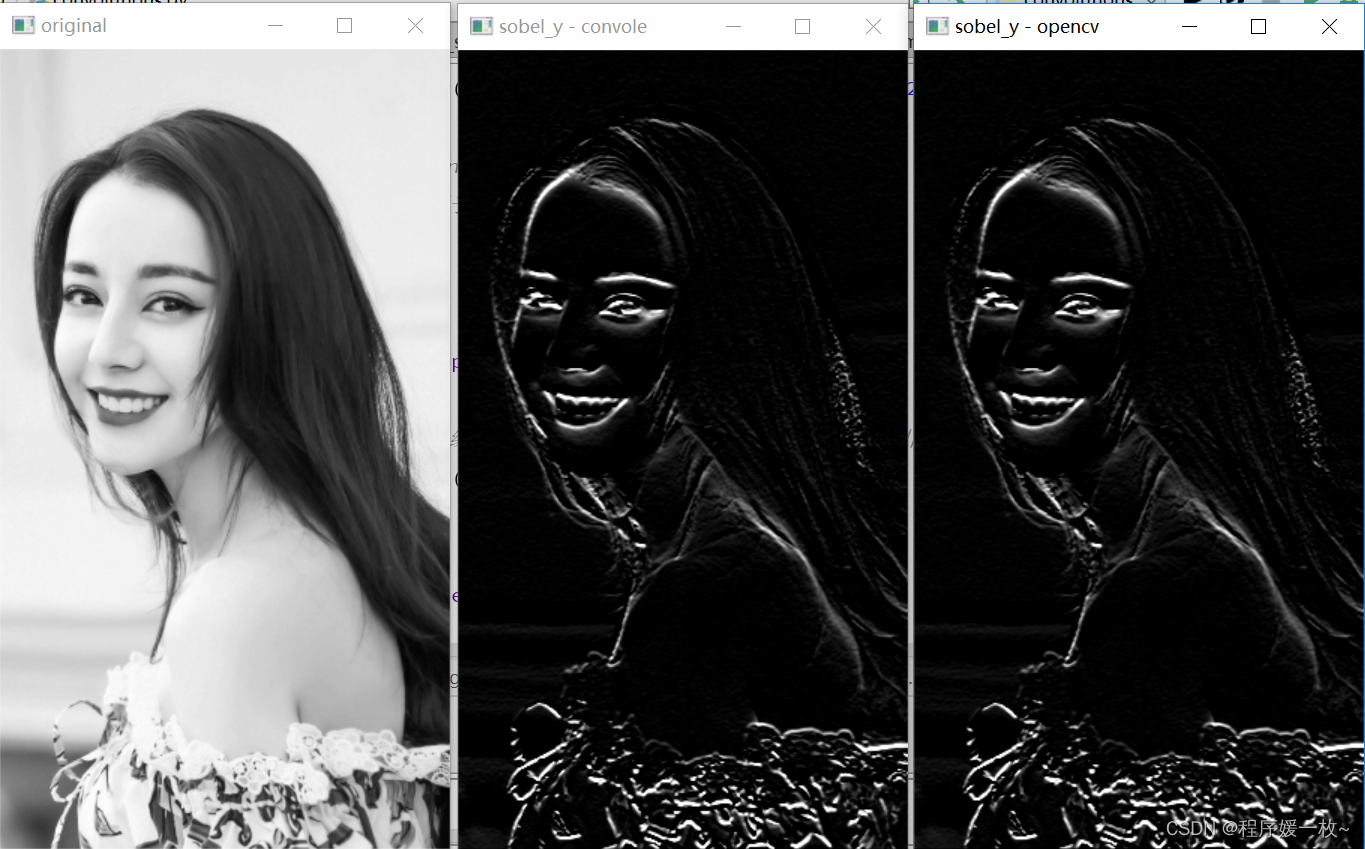
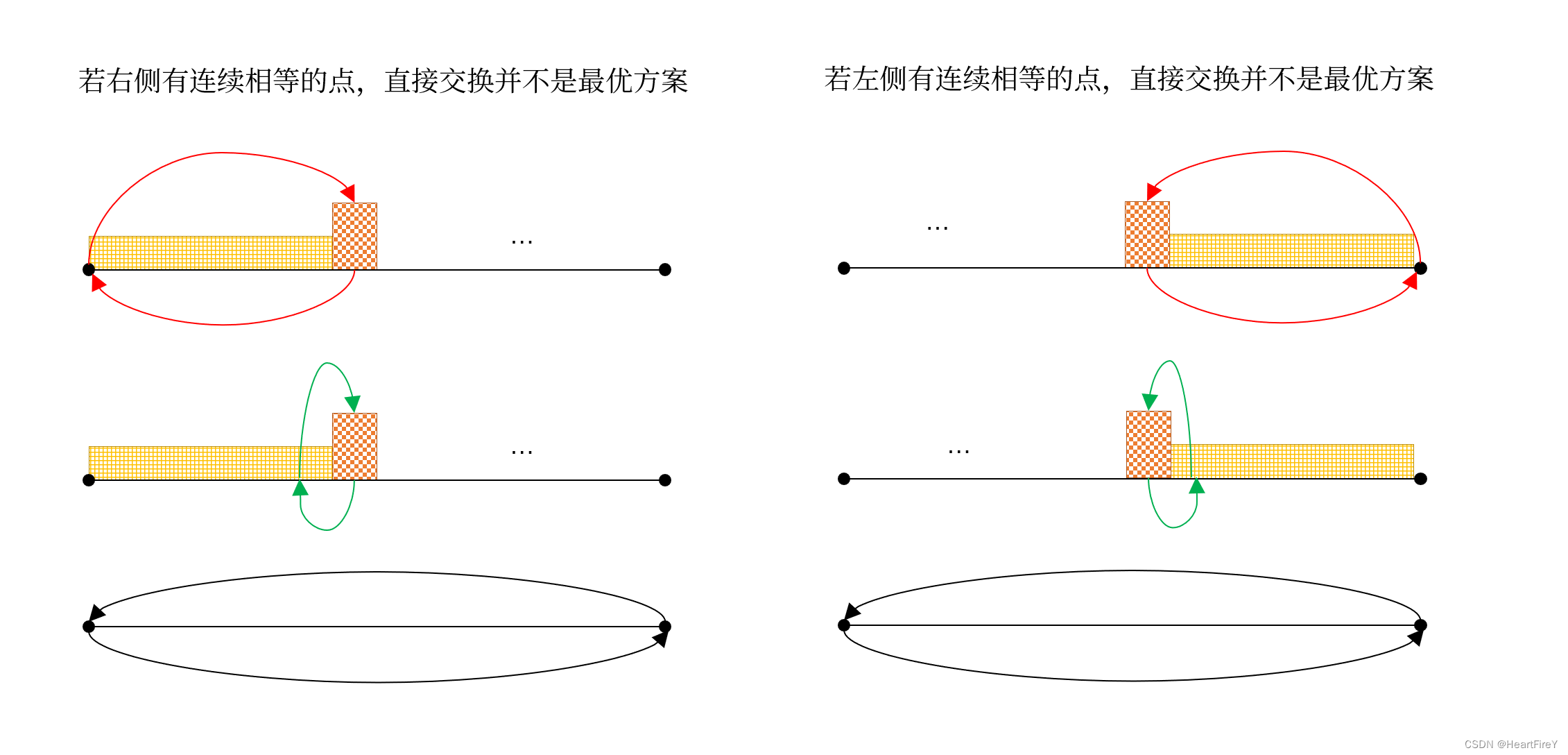
源代码:
C:\迅雷下载\2021072816023491335\59e95a4689eeb92f380f4ab2\202107\29976aaa-ef7a-11eb-aba5-00163e0a088c
PPT:
C:\迅雷下载\2021072816023491335\59e95a4689eeb92f380f4ab2\202009\942a5ce8-fe34-11ea-a6a1-00163e0396a1
参考文献:
C:\迅雷下载\2021072816023491335\59e95a4689eeb92f380f4ab2\202009\c53b3bcc-fe34-11ea-97a4-00163e0a088c
2.5 算法的特性
- 输入
- 输出
- 有穷性
- 确定性
- 可行性
2.6 算法设计的要求
- 正确性
- 可读性
- 健壮性
- 时间效率高和存储量低
2.9
推导大 O 阶方法
1)用常数 1 取代运行时间中的所有加法常数。
即,不论算法函数运行多少次,只要是通过加法得到的,就改为 1。
2)在修改后的运行次数函数中,只保留最高阶项
3)如果最高阶项存在且其系数不是 1,则去除与这个项相乘的系数。
得到的结果就是大 O 阶。
2.9.5 对数阶
2 x Count >= n 退出循环
由 2Count = n 得到 x = log2n,时间复杂度是 O(logn)
2.10 常见的时间复杂度
常数阶
12
O(1)
线性阶
2n + 3
O(n)
平方阶
3n2 + 2n + 1
O(n2)
对数阶
5log2n + 20
O(logn)
nlogn阶
2n + 3nlog2n + 19
O(nlogn)
立方阶
6n3 + 2n2 + 3n + 4
O(n3)
指数阶
2n
O(2n)
时间复杂度耗费的时间从小到大排:
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)
第3章,线性表
线性表:(List) 零个或多个元素的有限序列。
数组长度:存放线性表的存储空间的长度,存储分配后这个量一般是不变的。
线性表的长度:线性表中数据元素的个数,随着线性表插入和删除操作的进行,这个量是变化的。
任意时刻,线性表的长度应该小于等于数组的长度。
3.5 顺序存储结构的插入与删除
优点:
- 无须为表示表中元素之间的逻辑关系而增加额外的存储空间。
- 可以快速地存取表中任一位置的元素。
缺点: - 插入和删除操作需要移动大量元素。
- 当线性表长度变化较大时,难以确定存储空间的容量。
- 造成存储空间的“碎片”
3.6 线性表的链式存储结构
节点:
- 节点数据
- 下一节点地址
3.7 单链表的读取
要通过循环的移动下标,判断,才能读取到指定下标的数据。
3.8 单链表的插入与删除
3.9 单链表的整表创建
1)声明一指针 p 和计数器变量 l
2)初始化一空链表 L。
3)让 L 的头结点的指针指向 NULL,即建立一个带头结点的单链表。
4)循环:
(1)生成一新结点赋值给 p
(2)随机生成一数字赋值给 p 的数据域 p->data
(3)将 p 插入到头结点与前一新结点之间。
3.10 单链表的整表删除
3.12 静态链表
3.13 循环链表
3.14 双向链表
第4章,栈与队列
4.6 栈的链式存储结构及实现
4.8 栈的应用 —— 递归
4.9 栈的应用 —— 四则运算表达式求值
后缀表达式:叫后缀的原因,在于所有的符号都是在要运算数字的后面出现。
一种不需要括号的后缀表达法,称为逆波兰表示(Reverse Polish Notation, RPN)。
4.10 队列的定义
4.12 循环队列
第5章,串(字符串)
5.6 朴素的模式匹配算法
110页,
5.7 KMP 模式匹配算法
第6章,树
6.8.2 二叉树的遍历方法
[[二叉树的遍历方法]]
书中规则的描述认为不清晰。
6.9 二叉树的建立
6.11 树、森林与二叉树的转换
第7章,图
7.6 最小生成树
普里姆( Prim )算法
克鲁斯卡尔( Kruskal )算法
7.7 最短路径
迪杰斯特拉( Dijkstra )算法
弗洛伊德( Floyd )算法
7.8 拓扑排序
7.9 关键路径
第8章,查找
8.3 顺序表查找
8.4 有序表查找
8.5 线性索引查找
8.6 二叉排序树
8.7 平衡二叉树(AVL 树)
8.8 多路查找树(B树)
8.9 散列表查找(哈希表)概述
8.10 散列函数的构造方法
- 直接定址法:取关键字的某个线性函数值为散列地址
- 数字分析法
- 平方取中法
- 折叠法
- 除留余数法
- 随机数法
8.11 处理散列冲突的方法
- 开放定址法
- 再散列函数法
- 链地址法
- 公共溢出区法