AcWing245. 你能回答这些问题吗线段树详解

news2025/7/18 11:59:04

3.2线段树

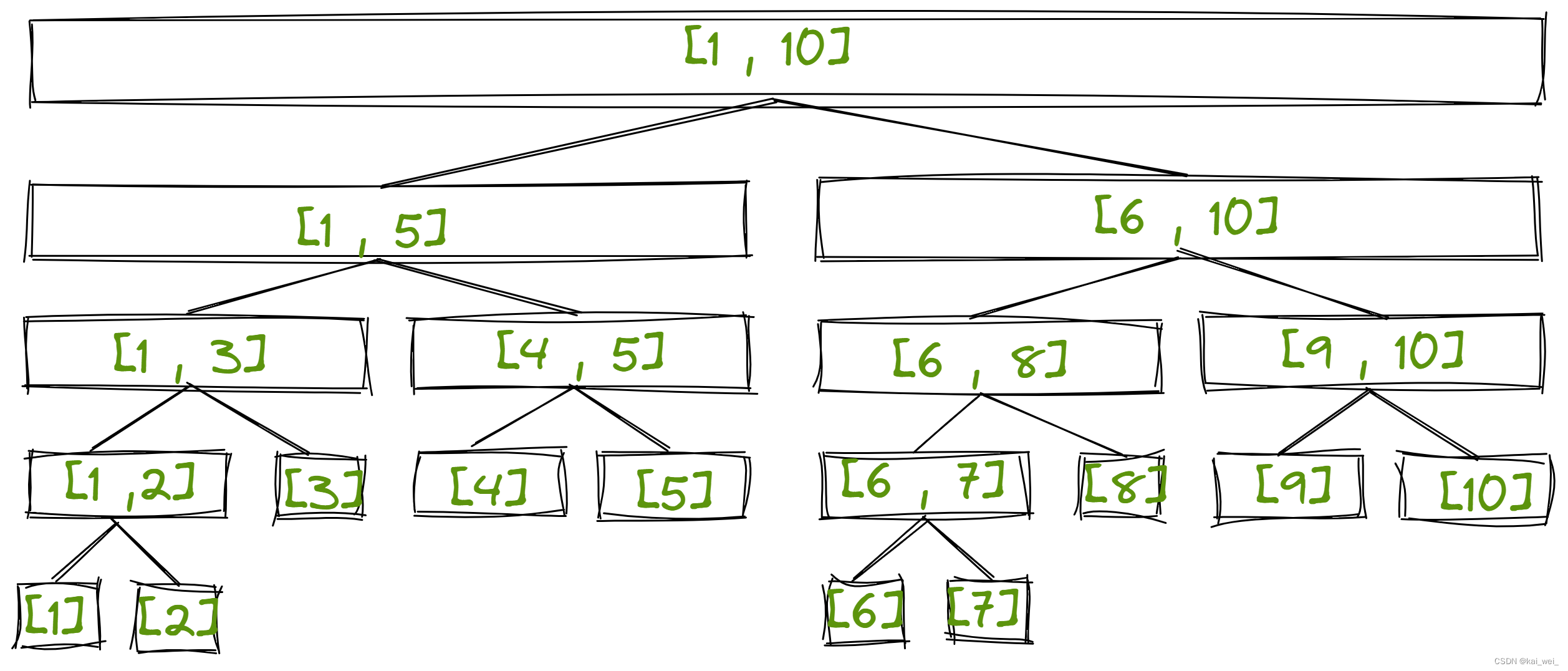
在这里插入图片描述

例题分析

245. 你能回答这些问题吗 - AcWing题库

**题意：**给一条序列，如何动态维护区间的最大子段和，包括询问某区间的最大字段和和修改某个数。

分析：线段树struct保留什么信息。能否通过左右儿子的这些信息求出父节点的所有信息。

首先毋庸置疑的是左右端点和最大连续子段和。

struct node{
	int l,r;
	int tmax;
}

然后我们思考，能不能得到父节点的信息。

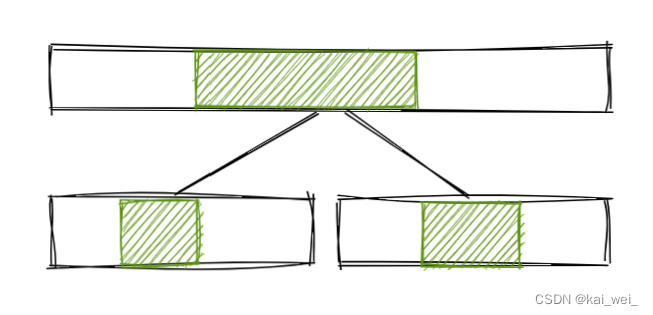
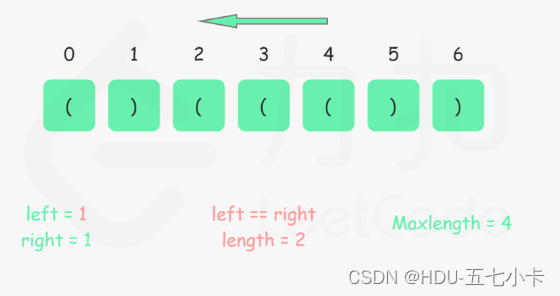
如图，假设我们已知左右孩子的最大子段和，同时假设父节点的最大字段和为图中绿色区域，我们发现，父节点的最大连续子段和可能是跨区间的，我们没办法通过孩子的信息得到父亲的信息，所以我们考虑添加维护的信息。

我们维护每个区间的最大前缀和和最大后缀和，如下图，横跨整个区间的子段和可以通过左边的最大后缀和加上右边的最大前缀和得到。

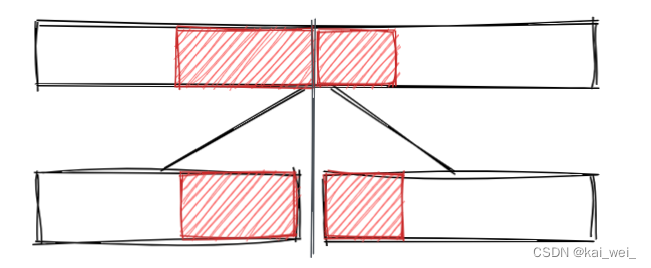
此时我们的结构体变成了这样：

struct node{
	int l,r;
	int tmax;//区间的最大字段和
	int lmax;//区间的最大前缀和
	int rmax;//区间的最大后缀和
}

那我们再回到刚才的思考，通过这些信息如何得到父节点的信息。

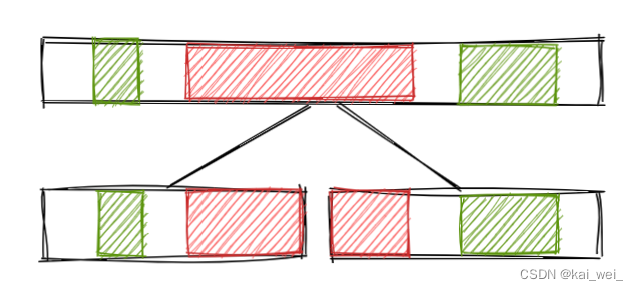
那么，结合三个信息，我们可以用三个值（左儿子的最大子段和、右儿子的最大子段和、左儿子的最大后缀和加右儿子的最大前缀和）取max来得到。这里信息全面吗？答案是全面的，不过是对于区间最大子段和来说；假设最大子段和在左区间，那么（如下图）1、2、3区间（前缀、中间、后缀）能够完全表示，4、5、6同理，除了这些情况，再加上跨区间的情况，那么这些情况取max就是确定的最大值。

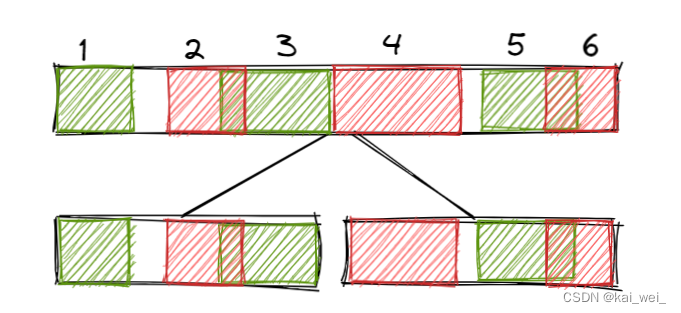
接下来我们再思考，我们新加入的两个信息是否能通过儿子节点求出来，假设我们的最大前缀和是跨区间的时候，那么情况变成了这样，所以我们还需要加一个信息：区间和。

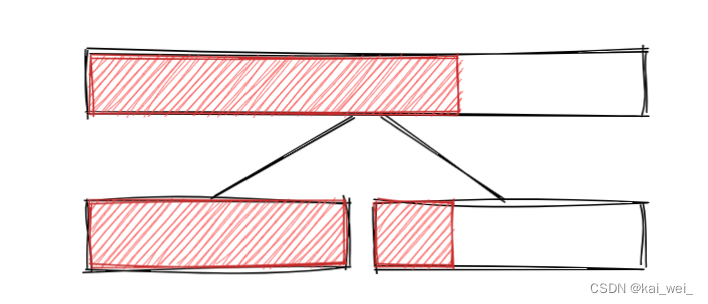
而区间和我们是可以直接求的，因此，我们每个信息都能得到了，分析完毕。

struct node{
	int l,r;
	int tmax;//区间的最大字段和
	int lmax;//区间的最大前缀和
	int rmax;//区间的最大后缀和
	int sum;//区间和
}

思考模式：首先我们想如何得到我们想要的答案，当添加了想要的信息之后，还要思考如何得到想要的信息，最后直到全部信息都能通过左右孩子得到。

参考代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 5e6 + 5;
vector<int> ve(N);
int n, k;

struct node {
    int l, r;
   	int tmax;//区间的最大字段和
	int lmax;//区间的最大前缀和
	int rmax;//区间的最大后缀和
	int sum;//区间和
} tr[4 * N];

void pushup(node& u, node& l, node& r) {//函数重载
    u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax);
    u.lmax = max(l.lmax, l.sum + r.lmax);
    u.rmax = max(r.rmax, r.sum + l.rmax);
    u.sum = l.sum + r.sum;
}

void pushup(int u) {
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r) {
    if (l == r) {
        tr[u]={l,r,ve[l],ve[l],ve[l],ve[l]};//到子节点直接存下所有信息
        return;
    }
    tr[u] = {l, r};
    int mid = l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    pushup(u);//这里想要pushup
}

node query(int u, int l, int r) {
    if (tr[u].l >= l && tr[u].r <= r)
        return tr[u];
    int mid = tr[u].l + tr[u].r >> 1;
    if (r <= mid)
        return query(u << 1, l, r);//答案完全在左区间
    else if (l > mid)
        return query(u << 1 | 1, l, r);//答案完全在右区间
    else{
        auto R = query(u << 1, l, r);
        auto L=query(u << 1 | 1, l, r); //答案想要左右区间的信息合并才能得到
        node res;
        pushup(res, R, L);//合并左右区间信息
        return res;
    }
}

void modify(int u,int x,int val){
    if(tr[u].l==x&&tr[u].r==x)
        tr[u] = {x,x,val,val,val,val};
    else{
        int mid = tr[u].l + tr[u].r >> 1;
        if(x<=mid)
            modify(u << 1, x, val);
        else
            modify(u << 1 | 1, x, val);
        pushup(u);
    }
}

int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) {
        cin >> ve[i];
    }
    //cout << "x" <<endl;
    build(1, 1, n);
    //cout << "x" << endl;
    for (int i = 1; i <= k; i++) {
        int q;
        cin >> q;
        if (q == 1) {
            int l, r;
            cin >> l >> r;
            if(l>r)
                swap(l, r);
            cout<<query(1, l, r).tmax<<endl;
        } else {
            int x, y;
            cin >> x >> y;
            modify(1, x, y);
        }
    }
}