第九章:堆排序与TOPK问题
- 一、堆排序:
- 1、思路分析:
- (1)建堆
- (2)排序
- 2、堆排序模板
- 二、TOPK问题:
- 1、什么是TOPK问题?
- 2、解决方法
一、堆排序:
假设我们实现一个小根堆,那么根节点就是最小值,那么我们存储这个最小值,再删除根节点,重新建堆,这样我们就能取得次小值。由此,我们发现,我们能够利用堆这种结构去进行数字的排序。
1、思路分析:
(1)建堆
我们先来分析一下刚才所说的逻辑,我们不断地建堆,删除堆顶,那么我们共需要建N个堆,每个堆所建成的时间是O(N)(后面会证明),那么此时的时间复杂度是N*O(N)=O(N2),这种思路所实现的堆排序效率太慢,那么我们该怎么做呢?接下来将为大家进行讲解:
堆排序的基础是将数组中的元素建成一个堆:
那么我们该如何建堆呢?
方式1:尾插

即我们从第一个元素开始,不断地插入新元素,然后让这个元素向上调整,让其对应到相应的位置。
void AdjustUp(int*arr,int child)
{
int parent=(child-1)>>1;
while(child>0)
{
if(arr[child]>arr[parent])
{
swap(arr[child],arr[parent]);
child=parent;
parent=(child-1)>>1;
}
else break;
}
}
void Heap_Sort(int*arr,int size)
{
//建堆
for(int i=0;i<size;i++)
{
AdjustUp(arr,i);
}
//.....
}
方式2:根节点向下调整
向下调整一般是针对根节点的,但是向下调整要保证下面紧跟的两个子树是两个堆,否则就会出错。因此,我们可以从倒数第二排开始,不断调整每一个小堆,从小到大,从少到多,如下图所示:
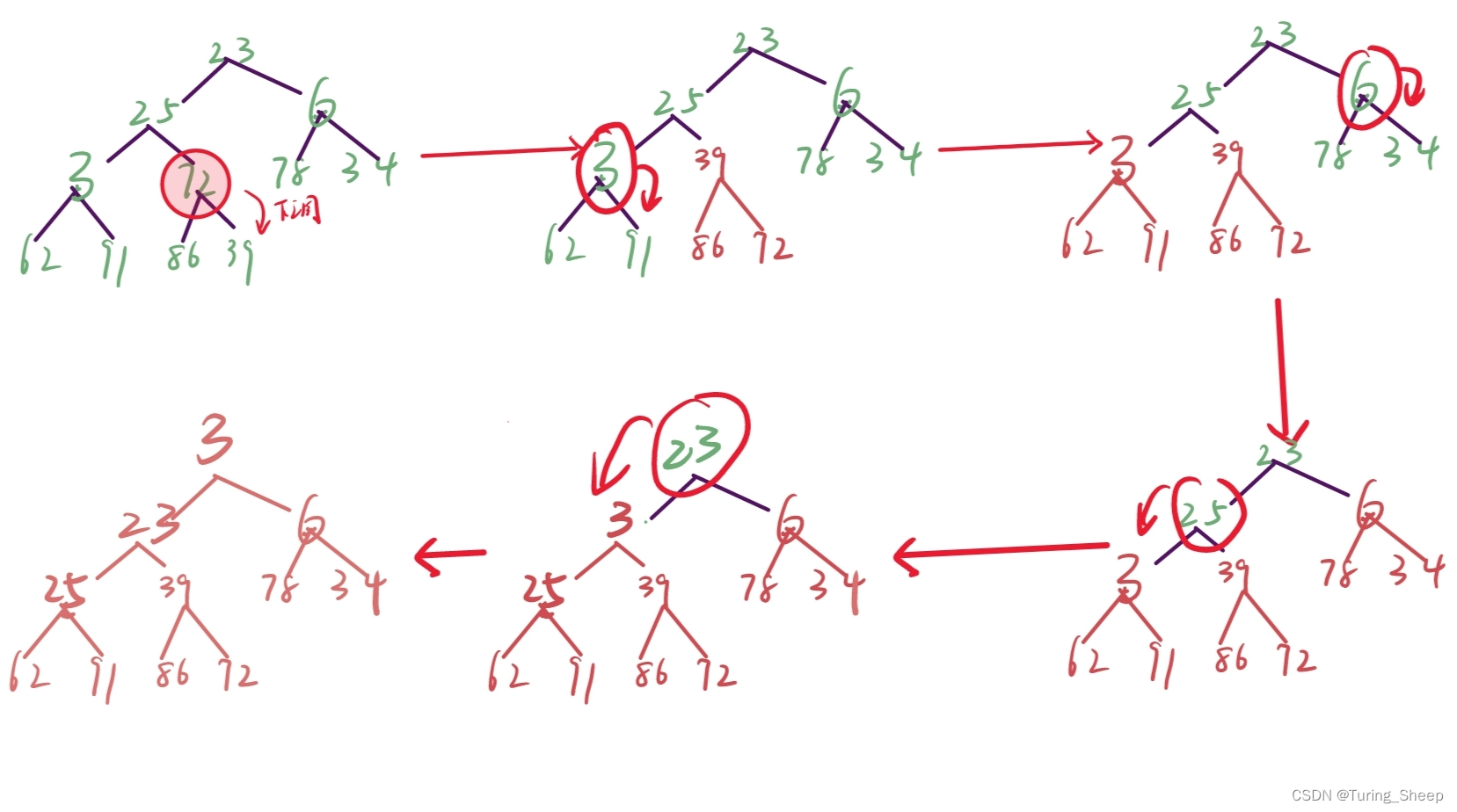
我们先保证两个子树是堆,然后再去调整这个两个子树的根节点。
void AdjustDown(int*arr,int size,int parent)
{
int child=parent*2+1;
while(child<size)
{
if(child+1<size&&arr[child+1]>arr[child])child++;
if(arr[child]>arr[parent])
{
swap(arr[child],arr[parent]);
parent=child;
child=parent*2+1;
}
else break;
}
}
void Heap_Sort(int*arr,int size)
{
//搭建一个大根堆
for(int i=(size-1-1)/2;i>=0;i--)
{
AdjustDown(arr,size,i);
}
//.........
}
很多人认为上述建堆的过程可能是N2,或者Nlog(N)。但是,实际上建堆的时间复杂度是O(N)
建堆的时间复杂度分析:


(2)排序
排序的话,假设我们是升序排列,但是我们创建的小根堆,那么每次取出根节点,但是取出之后,我们的堆的结构就混乱了,因此我们就需要重新建堆,此时的时间复杂度是n方。
于是我们换一个思路,我们创建一个大根堆,那么根节点就是最大的,我们让根节点和最后一个元素交换,然后我们删掉最后一个元素,即让尾指针前移,此时我们的最大值存储在了数组中的最后一位,然后我们让根节点向下移动,恢复堆的结构,此时堆顶就是次大值,然后我们再交换,让次大的元素到倒数第二的位置。由此类推,最后就能排好所有元素,其顺序为升序。
我们的根节点向下移动的时间复杂度是O(logN),共N个元素,此时时间复杂度是O(NlogN)。
我们升序排列用的是大根堆,降序排列用的是小根堆。
#include<iostream>
using namespace std;
void AdjustDown(int*arr,int size,int parent)
{
int child=parent*2+1;
while(child<size)
{
if(child+1<size&&arr[child+1]>arr[child])child++;
if(arr[child]>arr[parent])
{
swap(arr[child],arr[parent]);
parent=child;
child=parent*2+1;
}
else break;
}
}
//升序排序
void Heap_Sort(int*arr,int size)
{
//搭建一个大根堆:向下调整
//。。。。。。
//2、排序过程
for(int i=size-1;i>0;i--)
{
swap(arr[0],arr[i]);
AdjustDown(arr,i,0);
}
}
2、堆排序模板
#include<iostream>
#include<ctime>
using namespace std;
void AdjustDown(int*arr,int size,int parent)
{
int child=parent*2+1;
while(child<size)
{
if(child+1<size&&arr[child+1]>arr[child])child++;
if(arr[child]>arr[parent])
{
swap(arr[child],arr[parent]);
parent=child;
child=parent*2+1;
}
else break;
}
}
void Heap_Sort(int*arr,int size)
{
for(int i=(size-1-1)/2;i>=0;i--)
{
AdjustDown(arr,size,i);
}
for(int end=size-1;end>0;end--)
{
swap(arr[0],arr[end]);
AdjustDown(arr,end,0);
}
}
二、TOPK问题:
1、什么是TOPK问题?
topk问题就是,我们再一堆数字中选出前K个最大的或者最小的数字。此时,我们第一个想到的暴力方法就是将整体进行排序,如果用冒泡排序,其时间复杂度是N方,如果用的是快排,堆排其时间复杂度是nlogn。但是,整体上都是小题大作的,因为我们只需要知道前几个最大的,而不是将所用的数字都排序。
2、解决方法
看到这道题的题面,我们想到的应该是堆的特点,再堆中,我们再不作任何操作的情况下,我们只知道最大值是什么,或者最小值是什么,即根节点的值。
假设我们想要选出的是前几个最小的,那么我们可以建一个小根堆,然后不断地调用我们之前实现的堆数据结构中的两个接口函数,删除和打印,两个函数。
效果如下:
void test01()
{
Heap hp;
HeapInit(&hp);
HeapPush(&hp, 1);
HeapPush(&hp, 34);
HeapPush(&hp, 15);
HeapPush(&hp, 5);
HeapPush(&hp, 45);
HeapPush(&hp, 12);
HeapPush(&hp, 32);
HeapPrint(&hp);
HeapPop(&hp);
HeapPrint(&hp);
HeapPop(&hp);
HeapPrint(&hp);
HeapPop(&hp);
HeapPrint(&hp);
}
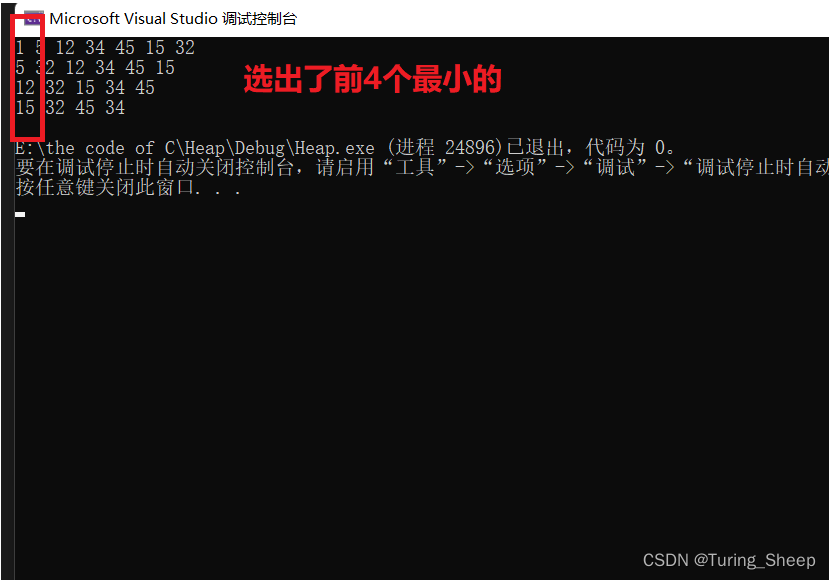
但是如果我们的数据量是十个亿,此时我们的内存区是不支持将其造成一个堆的,因此上述的方法就行不通了。那么我们该怎么办呢?
我们看下面的最终方案:动态堆
我们利用前k个元素创建一个元素个数为k的大根堆,那么我们堆中的较小元素一定会 “沉底”。此时,我们再去不断地读取元素,然后让这个元素和根节点比较,如果小于根节点,我们就替换掉根节点,然后让替换后的新的根节点下沉,为什么让这二者比较呢?因为我们创建的是大根堆,但是我们想要的是最小值,而根节点是最大的,所以根节点是最有可能被换掉的,所以我们让根节点去比较,最终剩下的这个元素为K的堆,就是答案。
// 在N个数找出最大的前K个 or 在N个数找出最小的前K个
void TopK(int* a, int n, int k)
{
HP hp;
HeapInit(&hp);
// 创建一个K个数的小堆
for (int i = 0; i < k; ++i)
{
HeapPush(&hp, a[i]);
}
// 剩下的N-K个数跟堆顶的数据比较,比他大,就替换他进堆
for (int i = k; i < n; ++i)
{
if (a[i] > HeapTop(&hp))
{
HeapPop(&hp);
HeapPush(&hp, a[i]);
}
}
HeapPrint(&hp);
HeapDestroy(&hp);
}