专攻超统一物理学的莲子,对机械结构的运动颇有了解。如下图所示,是一个三进制加法计算器的(超简化)示意图。
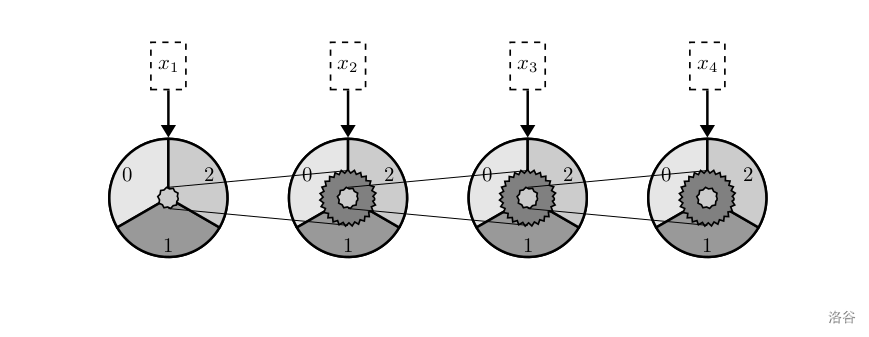
一个四位的三进制整数,从低到高位,标为 x_1,x_2,x_3,x_4x1,x2,x3,x4。换言之,这个数可以写成 \overline{x_4x_3x_2x_1}_{(3)}x4x3x2x1(3)。把它放在这四个齿轮里,对应箭头指向的数字就是现在这位的数值。
在这种机械式计算机里,我们通过齿轮的啮合来实现数位间的连接。通过不同齿轮半径的比例来确定进制。图中所有浅灰色的小齿轮的半径,比上使用皮带相接的较大齿轮的半径,都是 1:31:3。那么小齿轮每转动一圈,大齿轮就转动 \dfrac{1}{3}31 圈,也就是刚好一个数码的角度。
于是,我们通过控制齿轮的半径实现了 33 进制的进位。
如果需要实现三进制加法,则只需要在对应数位拨动对应的数码长度即可。
如下是个例子,实现 \overline{1021}_{(3)}+\overline{0021}_{(3)}=\overline{1112}_{(3)}1021(3)+0021(3)=1112(3)
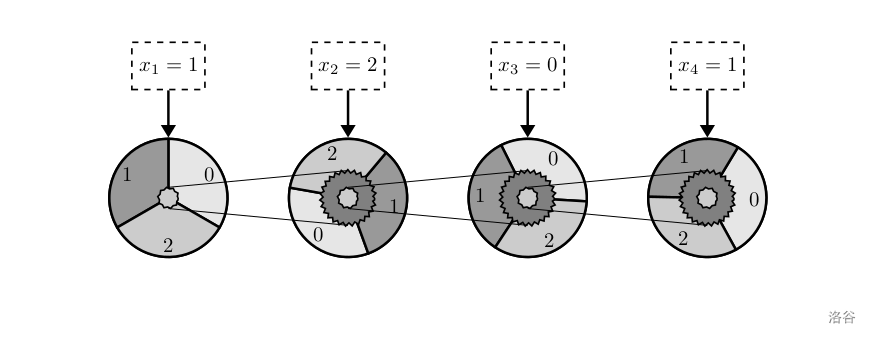
初始时齿轮的状态如上。

把第一个齿轮拨动一个单位长度,变为如上图所示。
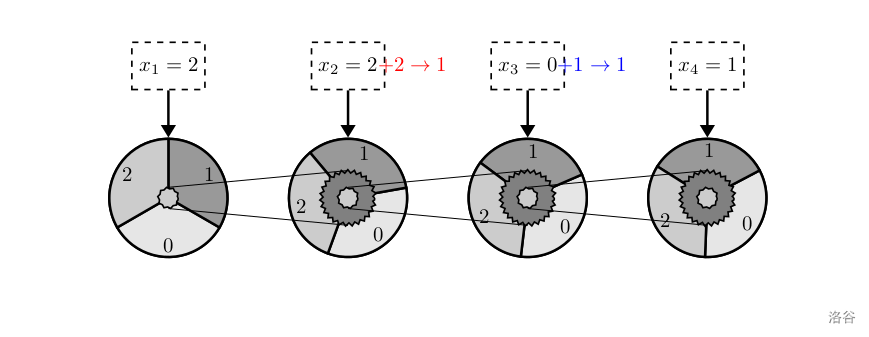
把第二个齿轮拨动两个单位长度,变为如上图所示。读数,得到结果 \overline{1112}_{(3)}1112(3)。
现在莲子设计了如下图所示的机械结构。对于从左往右数的第 ii 枚齿轮,它上面的浅色小齿轮与第 i+1i+1 枚齿轮上的深色小齿轮的半径之比为 1:(i+2)1:(i+2)。也就是说,第 ii 枚齿轮每转动 11 圈,第 i+1i+1 枚齿轮转过的角度恰好为它上面的一个数码。
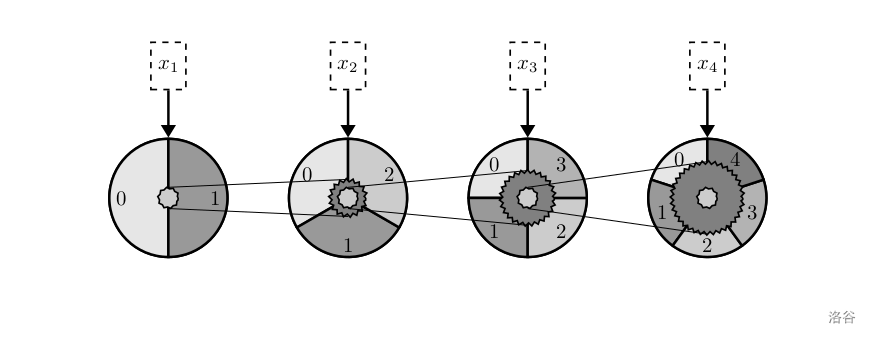
莲子想要知道,在这样的特别的进制表示下,给定 a,ba,b,那么计算出的 a+ba+b 的结果是多少。
题目描述
题目背景的问题可以转化为如下描述:
给定两个长度分别为 n,mn,m 的整数 a,ba,b,计算它们的和。
但是要注意的是,这里的 a,ba,b 采用了某种特殊的进制表示法。最终的结果也会采用该种表示法。具体而言,从低位往高位数起,第 ii 位采用的是 i+1i+1 进制。换言之,相较于十进制下每一位的「逢 1010 进 11」,该种进制下第 ii 位是「逢 i+1i+1 进 11」。
下图所示,左边是十进制的竖式加法;右边是这种特殊进制的竖式加法。图中的红色加号表示上一位发生了进位。
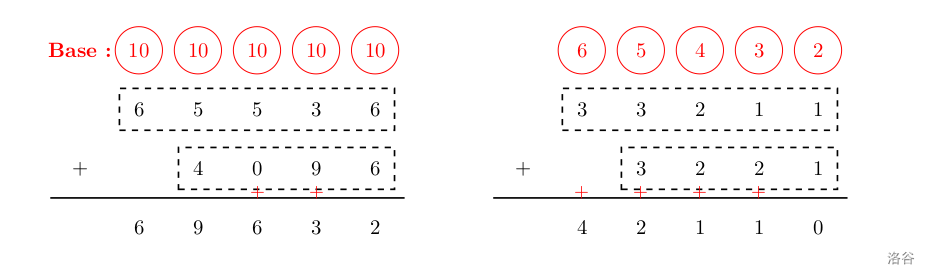
输入格式
- 第一行有两个整数 n,mn,m,分别表示 aa 和 bb 的位数。
- 第二行有 nn 个整数,中间用空格隔开,从高到低位描述 aa 的每个数码。
- 第三行有 mm 个整数,中间用空格隔开,从高到低位描述 bb 的每个数码。
输出格式
- 输出有若干个整数,从高到低位输出 a+ba+b 在这种特殊表示法下的结果。
输入输出样例
输入 #1复制
5 4 3 3 2 1 1 3 2 2 1
输出 #1复制
4 2 1 1 0
输入 #2复制
10 1 10 9 8 7 6 5 4 3 2 1 0
输出 #2复制
10 9 8 7 6 5 4 3 2 1
说明/提示
对于全部数据,保证 1\le n,m\le 2\times 10^51≤n,m≤2×105,从低位往高位数起有 a_i\in[0,i]ai∈[0,i],b_i\in[0,i]bi∈[0,i]。请使用 Java 或 Python 语言作答的选手注意输入输出时的效率。
#include <iostream>
#include <algorithm>
#include <climits>
#include <stdio.h>
#include <cstdlib>
#include <memory.h>
#include <queue>
#include <stack>
#include <math.h>
using namespace std;
//第二题
int main()
{
long long n, m;
cin >> n >> m;
//找到n和m哪个大
long long num;
if(n >= m) num = n;
else num = m;
//初始化
long long a[num+5], b[num+5], c[num+5];
memset(a, 0, sizeof(a));
memset(b, 0, sizeof(b));
memset(c, 0, sizeof(c));
//倒着输入
for(long long i = n; i > 0; i--)
cin >> a[i];
for(long long i = m; i > 0; i--)
cin >> b[i];
long long i = 1;
int sum;
int out = 0;
long long count1 = 2;
bool haha = false;
while(i <= num+1)
{
sum = (a[i]+b[i]+out)%count1; //获得该位的值
out = (a[i]+b[i]+out)/count1; //获得下一位该进的值
if(i == num && out >= 1) haha=true; //加起来是几位数
//cout << sum << ' ' << out <<endl;
count1++;
c[i++] = sum; //用c数组存储该位的值(向后逆序存储)
}
if(haha == true)
{
for(long long k = num+1; k > 0; k--)
{
cout << c[k] << ' ';
}
}
else
for(long long k = num; k > 0; k--)
{
cout << c[k] << ' ';
}
}