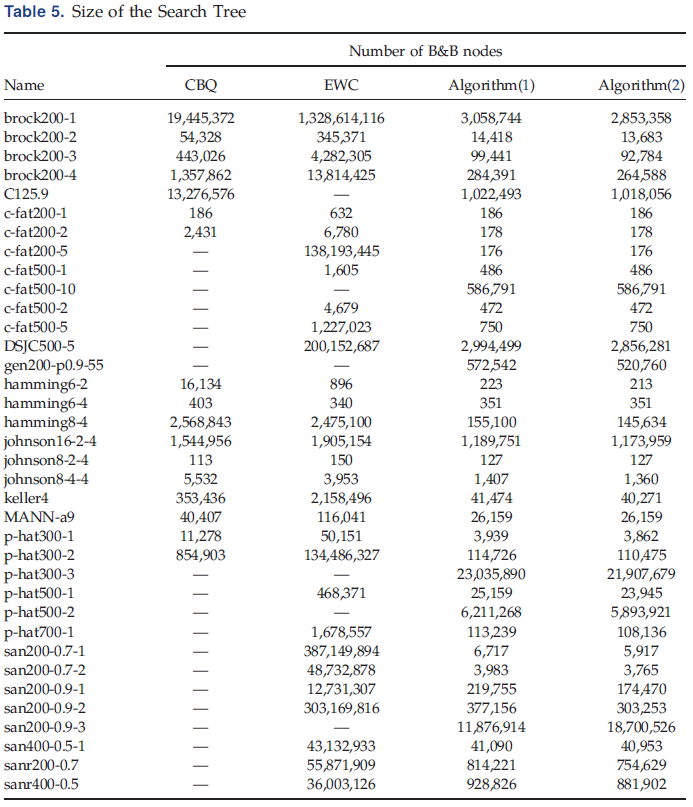
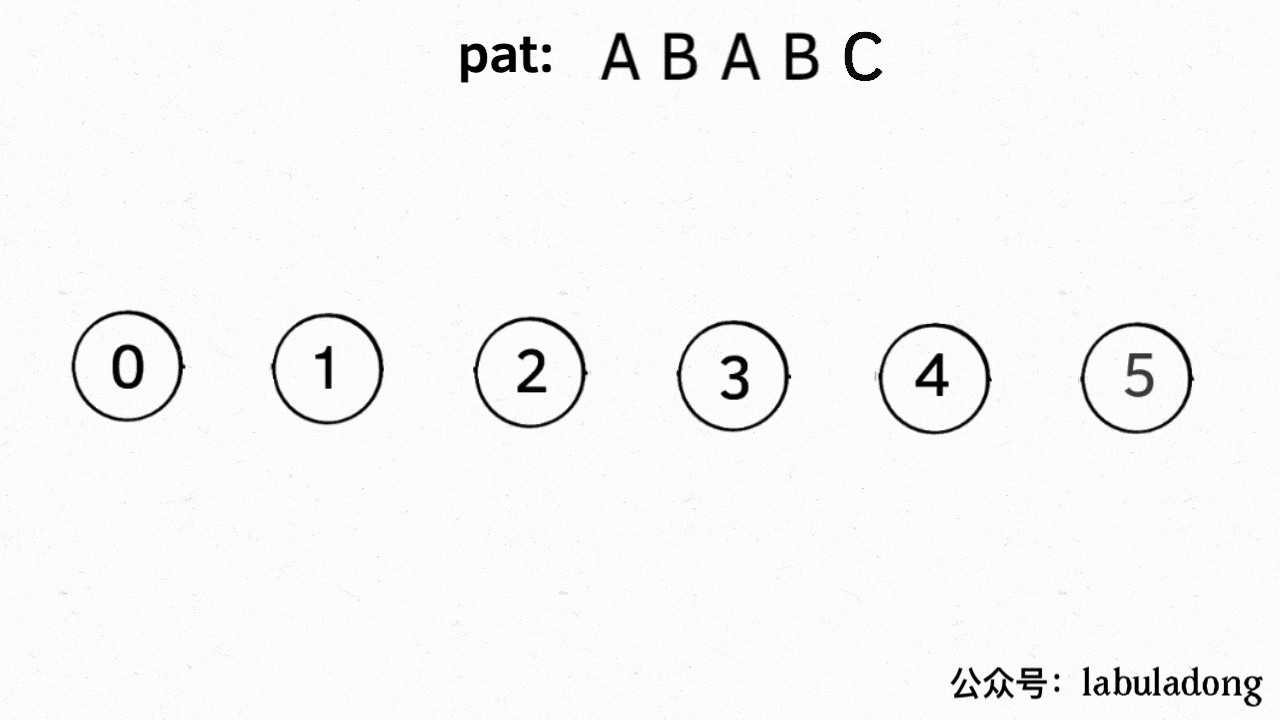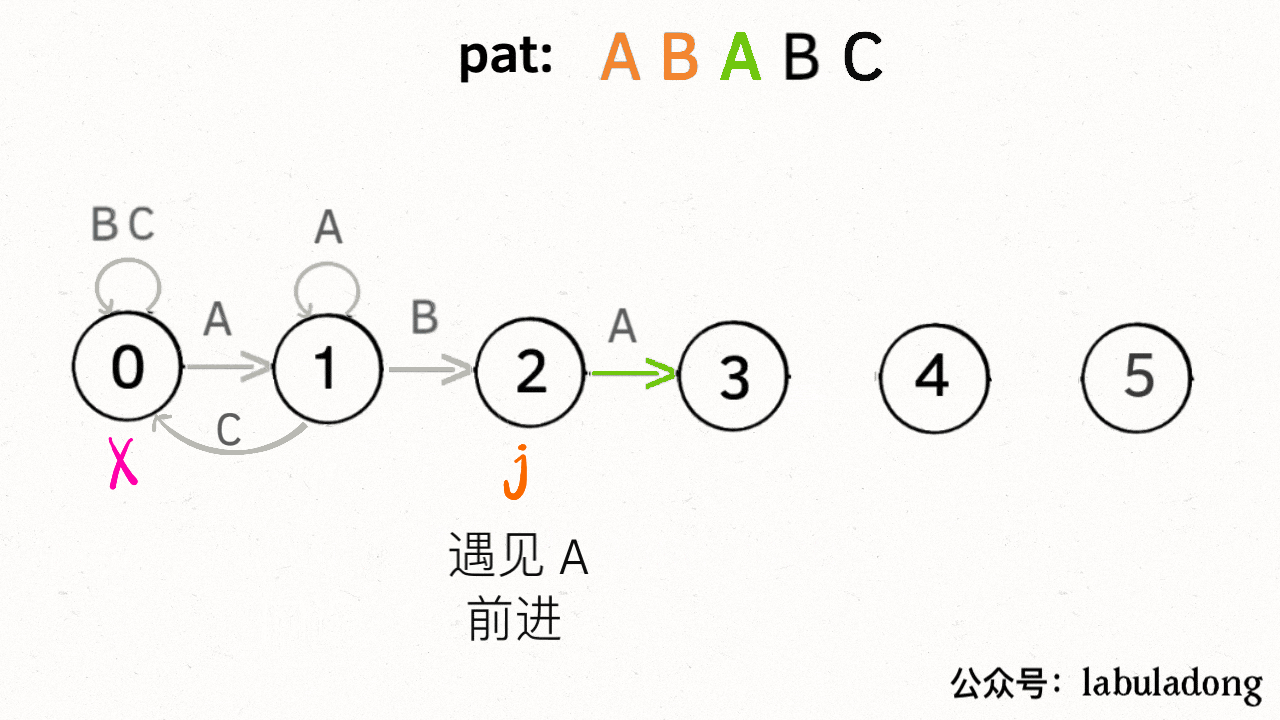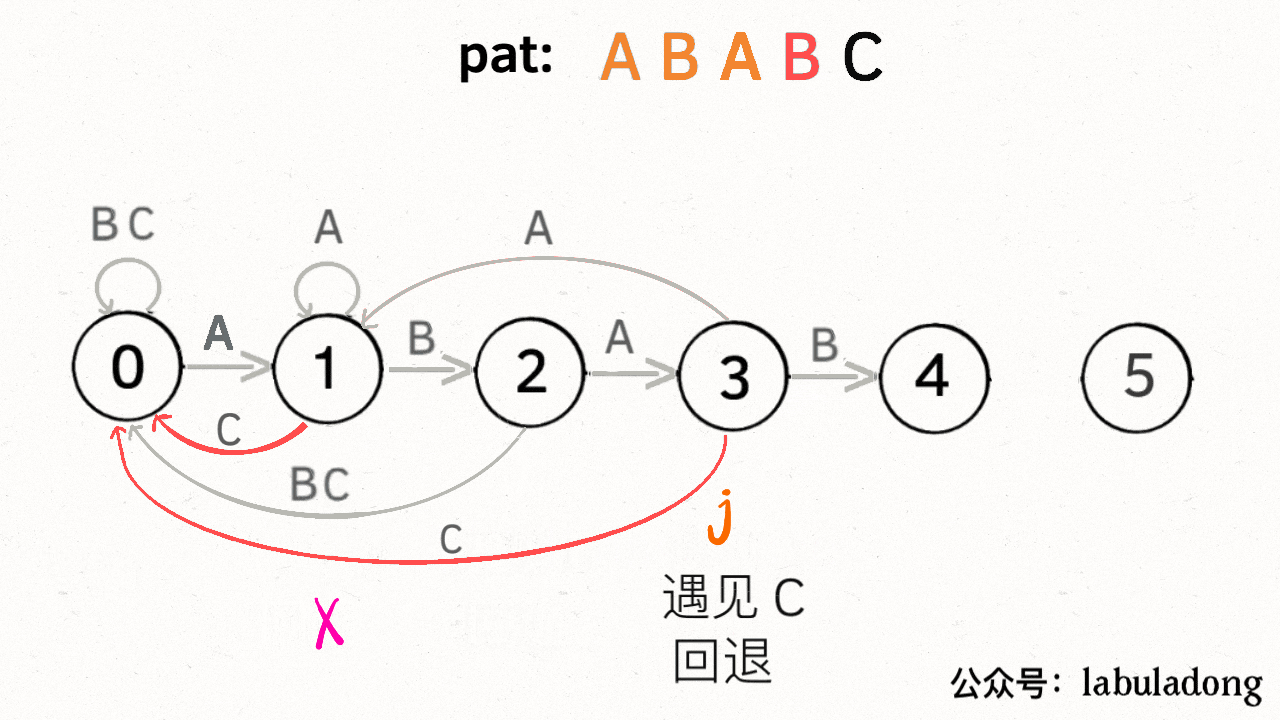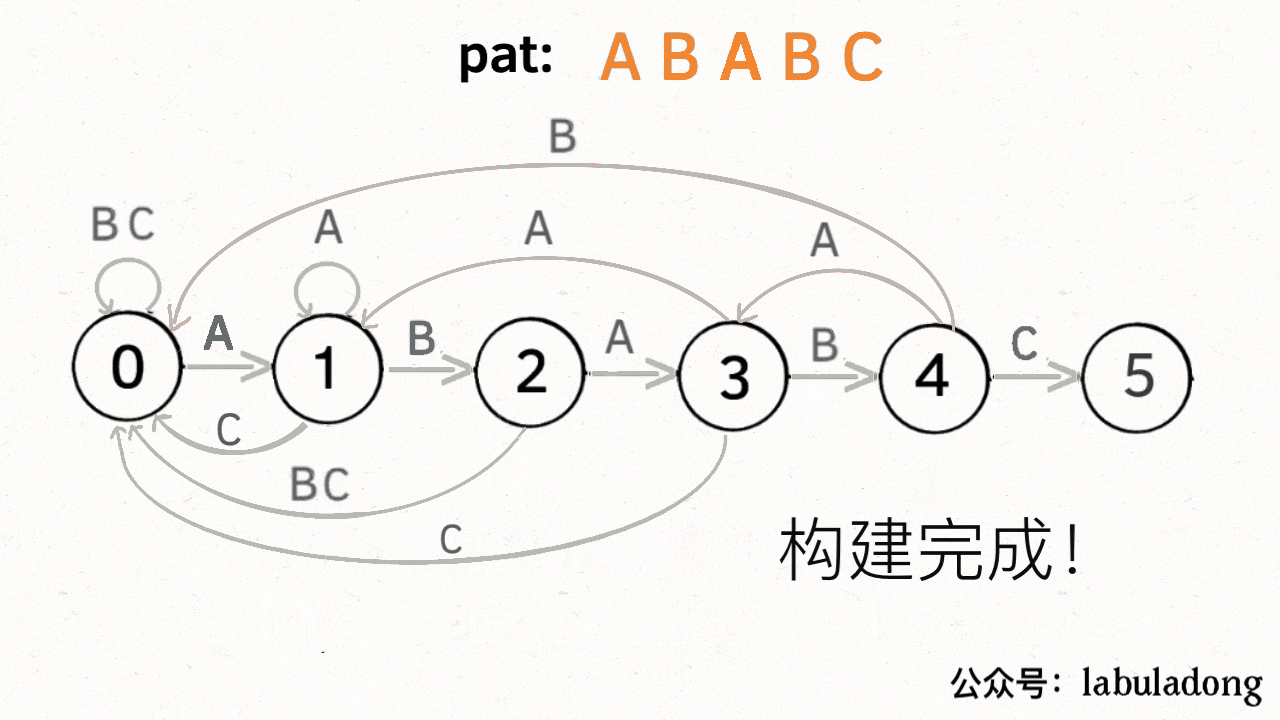
传统方案

if-else 在我们编程时出现的频率，无需我多赘述。当逻辑复杂时，我们会写出很多 if-else 语句，于是网络上充斥着大量的相关文章，教我们如何去除if-else，大多大同小异。

归结下来，无非是策略模式、责任链模式等套路，它们目的都是一样的，都希望把逻辑打散在一个个类中，再通过一个工厂或者什么别的玩意去调度它们。

这些策略可以很好的处理以下语句：

if (cond) {
    do
} else if (cond){
    do
} else if (cond){
    do
} else if (cond){
    do
} else {
    do
}

由于 go 本身是支持函数作为一等公民，所以不怎么需要面向对象语言的设计模式，Java 虽然需要通过一些设计模式的支持，但总归也不是很复杂，这里以 go 为例：

package main

type Cond func(param interface{}) bool
type Do func()

var cond1 = func(param interface{}) bool {
   return false
}

var do1 = func() {}

var condMap = map[Cond]Do{
   cond1: do1,
}

func main(){
    for k, v := range condMap {
       if k(param) {
          v()
       }
    }
}

我们把条件和动作设计成两个函数：Cond \ Do ，就可以用 Map 去存储和扩展它。
Cond 和 Do 可以无限的新增下去。

更多的思考🤔

以上传统方案做法上没什么问题，但在设计上，却存在两个问题：

一、存在过度设计的嫌疑

首先， 如果真的只是例子中这种扁平的（指一层）if-else，即使它加到 100 个，也不会很复杂，本来也就很符合人类的思维习惯，一个个往下看就是了（人类很喜欢顺序和规律）。

过度设计是指为不属于当前业务需求（或短期可预见的需求）进行设计，说白了就是臆想一些场景，去兼容这些场景做设计。

如果可以预见的，这些扁平的if-else不会有大量的新增、删除操作，那就没必要使用这些设计模式；如果可以预见这些 if-else 会大量新增、删除，或者会被其他人维护，那使用这些模式进行改造倒是可行的。

二、无法解决if-else嵌套问题

对于多层的if-else，示例代码如下：

if (cond){
    if (cond){
        do
    } else if (cond){
        if (cond) {
            do
        } else if (cond){
            if (cond) {
                do
            } else if (cond){
                do
            } else if (cond){
                if (cond) {
                    do
                } else if (cond){
                    do
                } else {
                    do
                }
            }
        } else {
            do
        }
    }
} else {
    do
}

相信这种嵌套的if-else才是日常开发经常碰到的情况，可能没有示例这么夸张，但我们可以看出，这种不太好用策略或者责任链去解决。

策略套策略？也层层嵌套下去？

这种代码会更加的复杂，还不如不重构。

新方案：分支树

思考一下，这种嵌套的 if-else 是不是构成了一棵分支树，树的叶子节点就是某种操作，树的非叶子节点就是某个判断。

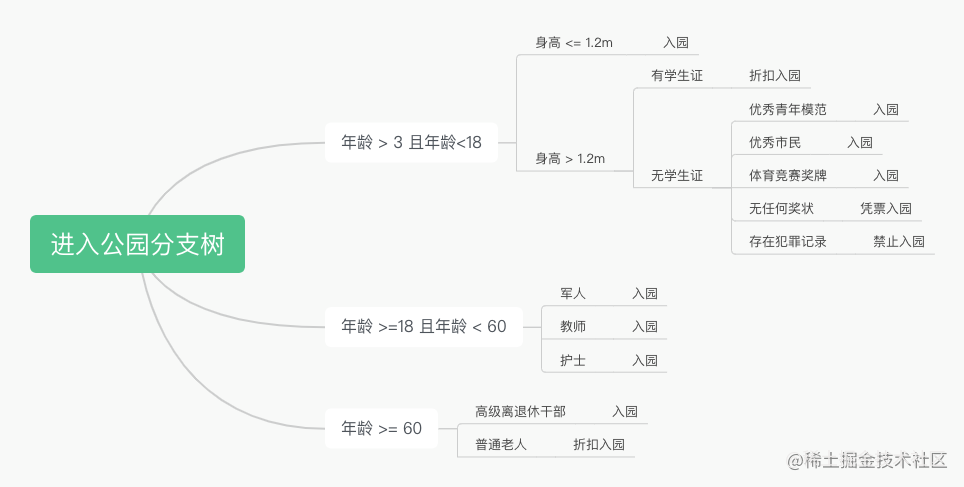
我们以一个日常生活场景：“入园政策”为例，这个场景就构成了一棵分支树。那么既然是树结构，我们就应该用树结构去表示它。

在机器学习中，也有相似的概念，称之为决策树。但是，机器学习的目标主要是怎么通过大量的数据，识别和构造出一个决策树，也就是图中这些条件本来是不存在的，需要通过学习去自动生成。而我们的场景是已存在 if-else 构成的分支树，我们要通过一种树结构去优化表示它。所以目的是不同的，我也用了新的名字：分支树。

要构造这样一棵分支树，我们先规定好树节点，分为两类：决策节点和叶子节点。决策节点负责判断数据是否符合条件，是则进入它的子节点，否则访问它的下个兄弟节点；叶子节点包含执行逻辑，一个个决策节点走下来，最终一定要走到一个叶子节点，不然这棵树就没有意义。

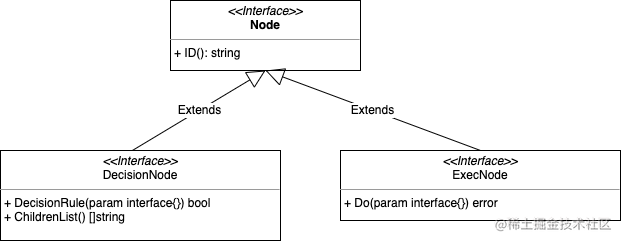
节点接口定义如上，DecisionRule 用来决策，ChildrenList 用于构造树。抽象了一个 Node，用于标识节点。

这里我原本想试试把接口方法中的 interface{} 换成泛型参数[T any]，但实际上做不到。似乎是 Go 不支持这种泛型方法，各位可以试试。

有了节点，我们接下来要实现这棵分支树：

如同我们实现一棵二叉树一样，我们一般都会定义一个根节点，它起到一个引领作用，没有根节点，我们无法拿到这个树。

我们还定义了一个节点 Map，保存了这棵树的所有节点，这与一般的树实现不同，这是为什么呢？

这是为了松耦合，我们在前面的接口定义中，将ChildrenList的返回值规定为[]string，也就是不需要返回 Node 结构，只需要返回 ID 标识。这样，我们就无需一定要先定义出叶子节点，只需要规定好叶子节点的 ID 标识。

这样的话，我们不需要从下到上的顺序去实现树的节点，而是可以以任意顺序，只要 ID 能对的上即可。所以我们需要一个节点 Map，能够根据 ID 标识去找到这个节点。

AddNode() 可以添加一个节点到树中，AddNode 会自动识别，把节点放在它在树中的正确位置。

当树的所有节点都添加好了，调用 Decision() ，遍历这个分支树，遍历到某个叶子节点，就会执行它的 Do 函数。这个遍历我们应该选用 BFS 遍历，不能使用 DFS 遍历，因为我们要一层一层的处理。

我们用一个实际的分支树来做个例子：

//                                           ┌──────┐
//                                           │ Root │
//                                           └──────┘
//                                               ▲
//                  ┌────────────────────────────┼──────────────────────┐
//                  │                            │                      │
//           ┌────────────┐          ┌───────────────────────┐   ┌─────────────┐
//           │  age < 18  │          │ age >= 18 & age < 60  │   │  age >= 60  │
//           └────────────┘          └───────────────────────┘   └─────────────┘
//                  ▲                            ▲                      ▲
//          ╱──────╱ ╲──────╲                    │                      │
//         ╱                 ╲            ╔════════════╗       ╔═════════════════╗
// ┌───────────────┐ ┌───────────────┐    ║ buy ticket ║       ║ discount ticket ║
// │ height < 1.2  │ │ height >= 1.2 │    ╚════════════╝       ╚═════════════════╝
// └───────────────┘ └───────────────┘
//         ▲                 ▲
//         │                 │
//    ╔═════════╗     ╔════════════╗
//    ║  enter  ║     ║ buy ticket ║
//    ╚═════════╝     ╚════════════╝

使用步骤如下代码所示：

func main() {
   tree := branch_tree.DecisionTree{}

   // 1. 定义叶子节点
   // 如上所说，我们例子里虽然先定义了叶子节点，但实际上这个顺序是可以打乱的
   enterNode := &EnterPark{}
   buyTicketNode := &BuyTicket{}
   discountTicketNode := &DiscountTicket{}

   // 2. 定义决策节点
   lessHeight := &HeightDecisionNode{
      Id: "H<120cm",
      DecisionFunc: func(param interface{}) bool {
         if p, ok := param.(*People); ok {
            return p.Height < 120
         }
         return false
      },
      Childs: []string{enterNode.ID()},
   }
   geHeight := &HeightDecisionNode{
      Id: "H>=120cm",
      DecisionFunc: func(param interface{}) bool {
         if p, ok := param.(*People); ok {
            return p.Height >= 120
         }
         return false
      },
      Childs: []string{buyTicketNode.ID()},
   }

   ageLess18 := NewAgeDecisionNode(0, 18)
   ageIn18And60 := NewAgeDecisionNode(18, 60)
   ageG60 := NewAgeDecisionNode(60, math.MaxInt)

   ageLess18.SetChilds([]string{lessHeight.ID(), geHeight.ID()})
   ageIn18And60.SetChilds([]string{buyTicketNode.ID()})
   ageG60.SetChilds([]string{discountTicketNode.ID()})
   

   // 3. 把以上节点加到树中
   err := tree.AddNode(enterNode)
   err = tree.AddNode(buyTicketNode)
   err = tree.AddNode(discountTicketNode)
   err = tree.AddNode(lessHeight)
   err = tree.AddNode(geHeight)
   err = tree.AddNode(ageLess18)
   err = tree.AddNode(ageIn18And60)
   err = tree.AddNode(ageG60)
   if err != nil {
      panic(err)
   }

   // 4. 接下来把数据输入到树中决策。
   err = tree.Decision(&People{
      Age:    16,
      Height: 150,
   })
   if err != nil {
      panic(err)
   }
   // 应该执行：Buy ticket

   err = tree.Decision(&People{
      Age:    8,
      Height: 110,
   })
   if err != nil {
      panic(err)
   }
   // 应该执行：Enter

   err = tree.Decision(&People{
      Age:    61,
      Height: 160,
   })
   if err != nil {
      panic(err)
   }
   // 应该执行：Discount

   err = tree.Decision(&People{
      Age:    45,
      Height: 160,
   })
   if err != nil {
      panic(err)
   }
   // 应该执行：Buy ticket

   // Run result:
   // I will buy ticket.
   // I will enter park.
   // I will discount.
   // I will buy ticket.
}

所有代码均在 Github 开源，欢迎 Star。

感谢观看~ 🎶

求职（远程、Golang）启事
本人非 985、211，普通本科大学，无大厂经历😂。
有一颗对技术充满热情的心和喜欢独立思考的大脑，单兵作战能力强。
SAIL作者，设计开发过多款业务、技术系统，也经历过高并发的洗礼。
如果您愿意让我成为您的同事，可私聊我或者通过邮箱（690174435@qq.com）与我联系。