前言
- 群智能算法(全局最优):模拟退火算法(Simulated annealing,SA),遗传算法(Genetic Algorithm, GA),粒子群算法(Particle Swarm Optimization,PSO)
- 局部搜索算法(local search algorithm):爬山算法 (Hill Climbing),禁忌算法(Tabu Search,TS)
- 路径搜索算法:A* Search
模拟退火算法
模拟退火算法(Simulate Anneal,SA)是一种通用概率演算法,用来在一个大的搜寻空间内找寻命题的最优解。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法。模拟退火算法是解决TSP问题的有效方法之一。
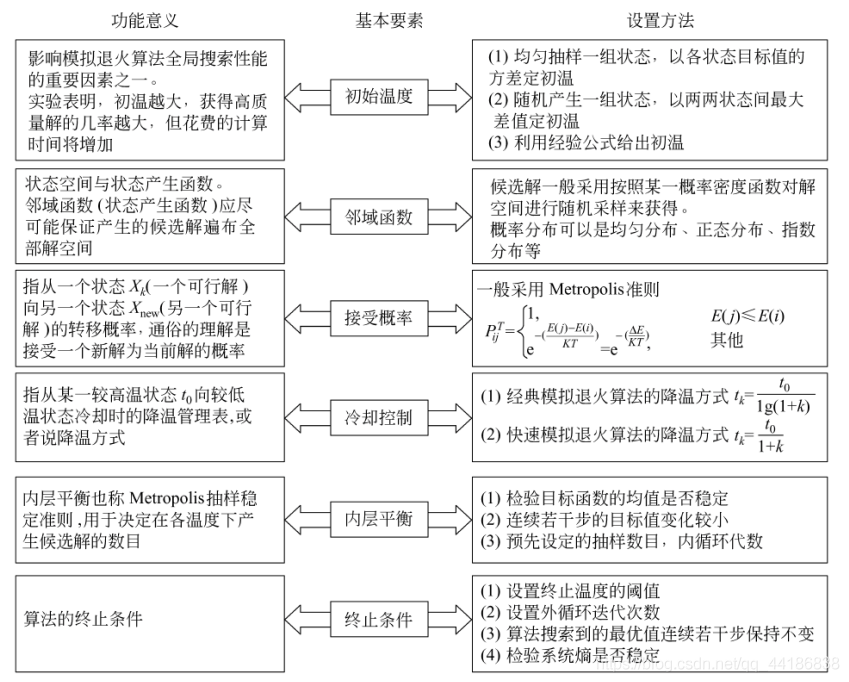
- 初始温度 T0、降温系数 Δ(0到1之间)、终止温度 Tk
- (外层循环)降温过程:每次T乘上Δ,直到 T≤Tk
- (内层循环)概率选择新解:在温度T时,选择领域解进行判断,优解直接接受,对于劣解,概率接受(T 越大时概率越大,新解和旧解差绝对值越小时概率越小)
过程详解
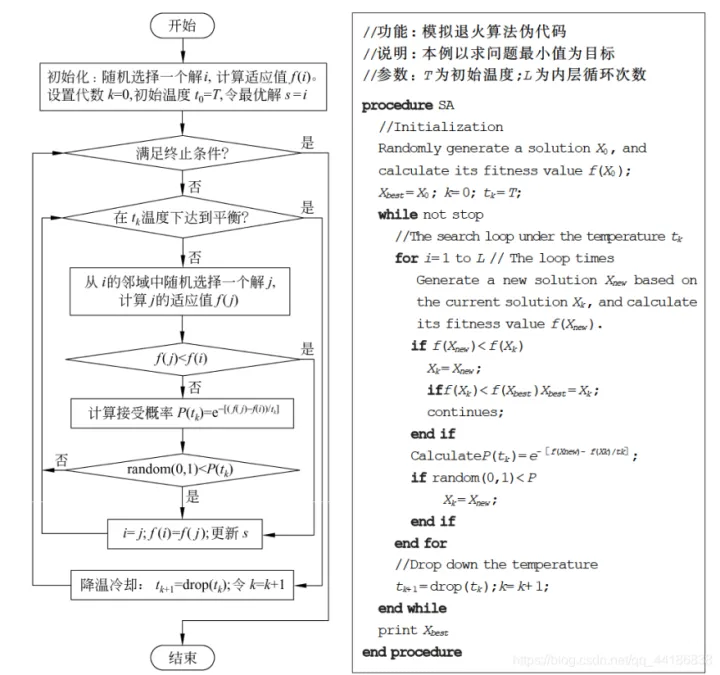
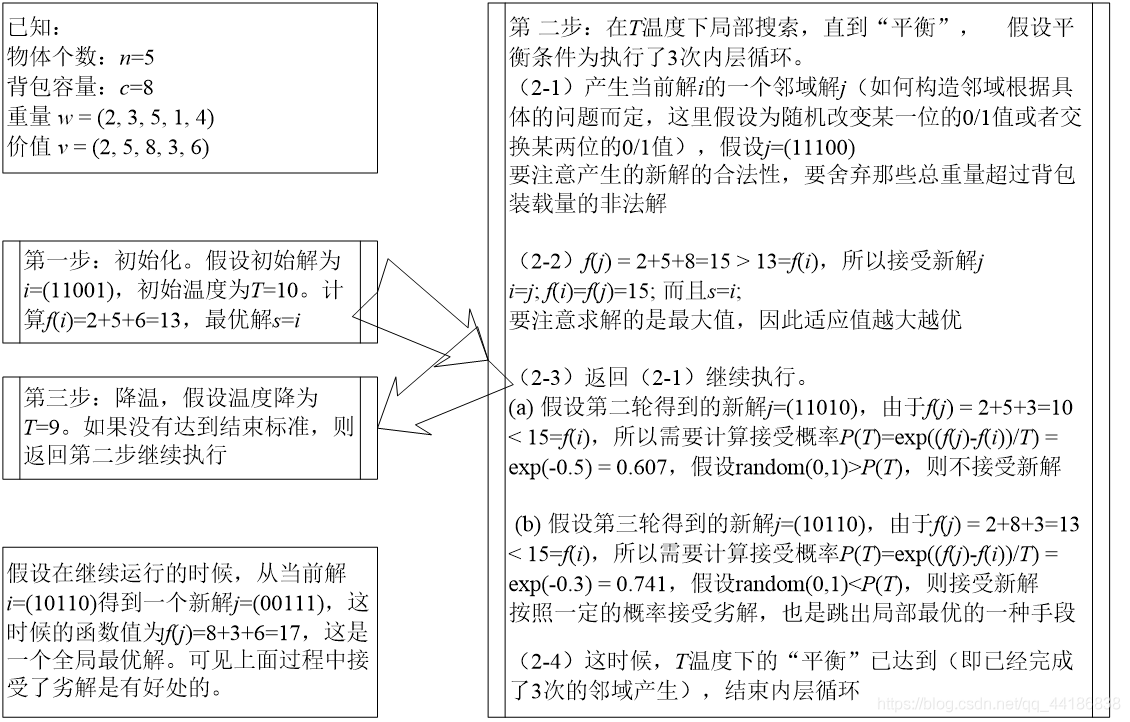
实际案例 - 背包问题
代码
class SimulatedAnnealing(object):
def __init__(self, weight_list, volume_list, value_list, Weight_threshold_value, Volume_threshold_value, satisfying_value, break_T):
"""背包物体属性"""
self.object_total_number = len(weight_list)
self.weight_list = weight_list
self.volume_list = volume_list
self.value_list = value_list
self.Weight_threshold_value = Weight_threshold_value
self.Volume_threshold_value = Volume_threshold_value
self.best_value = -1 # 更新最优值
self.cur_total_weight = 0
self.cur_total_volume = 0
self.cur_total_value = 0
self.best_indexs_way = [0] * self.object_total_number
self.current_indexs_way = [0] * self.object_total_number # best_way 记录全局最优解方案 now_way 记录当前解方案
self.weight = self.weight_list
self.value = self.value_list
self.volume = self.volume_list
"""跳出条件"""
self.satisfying_value = satisfying_value
self.break_T = break_T
"""模拟退火属性"""
self.T = 200.0 # 温度
self.af = 0.95 # af退火率
self.balance = 500 # 平衡次数
self.iter_times = 100 # 迭代次数
def initialize(self):
"""初始化,产生随机解"""
while True:
for k in range(self.object_total_number):
if random.random() < 0.5:
self.current_indexs_way[k] = 1
else:
self.current_indexs_way[k] = 0
self.calculate_value(self.current_indexs_way)
if self.cur_total_weight < self.Weight_threshold_value and self.cur_total_volume < self.Volume_threshold_value:
break
self.best_value = self.calculate_value(self.current_indexs_way)
self.copy_list(self.best_indexs_way, self.current_indexs_way)
def copy_list(self, a, b): # 复制函数 把b列表的值赋值a列表
for i in range(len(a)):
a[i] = b[i]
def calculate_value(self, x):
"""计算背包的总重量、总体积、总价值"""
self.cur_total_weight = 0
self.cur_total_volume = 0
self.cur_total_value = 0
for i in range(self.object_total_number):
self.cur_total_weight += x[i] * self.weight[i] # 当前总重量
self.cur_total_volume += x[i] * self.volume[i] # 当前总体积
self.cur_total_value += x[i] * self.value[i] # 当前总价值
return self.cur_total_value
def get_object(self, x): # 随机将背包中已经存在的物品取出
while True:
ob = random.randint(0, self.object_total_number - 1)
if x[ob] == 1:
x[ob] = 0
break
def put_object(self, x): # 随机放入背包中不存在的物品
while True:
ob = random.randint(0, self.object_total_number - 1)
if x[ob] == 0:
x[ob] = 1
break
def run(self):
self.initialize() # 初始化,产生初始解
for i in range(self.iter_times):
test_indexs_way = [0] * self.object_total_number
now_total_value = 0 # 当前背包价值
for i in range(self.balance):
now_total_value = self.calculate_value(self.current_indexs_way)
self.copy_list(test_indexs_way, self.current_indexs_way)
ob = random.randint(0, self.object_total_number - 1) # 随机选取某个物品
if test_indexs_way[ob] == 1: # 如果物品在背包中
self.put_object(test_indexs_way) # 随机放入背包中不存在的物品
test_indexs_way[ob] = 0 # 在背包中则将其拿出,并加入其它物品
else: # 不在背包中则直接加入或替换掉已在背包中的物品
if random.random() < 0.5:
test_indexs_way[ob] = 1
else:
self.get_object(test_indexs_way)
test_indexs_way[ob] = 1
temp_total_value = self.calculate_value(test_indexs_way)
if self.cur_total_weight > self.Weight_threshold_value or self.cur_total_volume > self.Volume_threshold_value:
continue # 非法解则跳过
if temp_total_value > self.best_value: # 如果新的解更好,更新全局最优
self.best_value = temp_total_value
self.copy_list(self.best_indexs_way, test_indexs_way)
if temp_total_value > now_total_value: # 如果新的解比当前解更好,直接接受新解
self.copy_list(self.current_indexs_way, test_indexs_way)
else:
g = 1.0 * (temp_total_value - now_total_value) / self.T
if random.random() < math.exp(g): # 概率接受劣解
self.copy_list(self.current_indexs_way, test_indexs_way)
self.T = self.T * self.af # 温度下降
"""跳出条件, 达到满意的解或者温度直接跳出"""
if self.best_value > self.satisfying_value or self.T < self.break_T:
break
# 方案转为索引的形式
best_object_number = []
for i in range(object_total_number):
if self.best_indexs_way[i]:
best_object_number.append(i)
print(f"最好的选择方案是取第best_object_number:{best_object_number}个物品,total_value:{self.best_value}")import random, math
object_total_number=9
weight_list = random.sample(range(1, 100), object_total_number)
volume_list = random.sample(range(1, 100), object_total_number)
value_list = random.sample(range(1, 1000), object_total_number)
Weight_threshold_value = sum(weight_list) / 2 # 取总和值的一半算了?直接不用改动了
Volume_threshold_value = sum(volume_list) / 2
print(f"Weight_threshold_value:{Weight_threshold_value}")
print(f"Volume_threshold_value:{Volume_threshold_value}")
print(f"weight_list:{weight_list}")
print(f"volume_list:{volume_list}")
print(f"value_list:{value_list}")
satisfying_value = 999999 # 设置满意解,达到就直接退出了
break_T = 1 # 设置跳出温度
SimulatedAnnealing_obj = SimulatedAnnealing(weight_list=weight_list, volume_list=volume_list, value_list=value_list,
Weight_threshold_value=Weight_threshold_value,
Volume_threshold_value=Volume_threshold_value,
satisfying_value=satisfying_value, break_T=break_T)
SimulatedAnnealing_obj.run()输出结果:
Weight_threshold_value:258.0 Volume_threshold_value:228.0 weight_list:[53, 71, 16, 66, 74, 75, 55, 18, 88] volume_list:[46, 41, 31, 15, 21, 47, 78, 89, 88] value_list:[732, 886, 98, 889, 128, 966, 355, 140, 491] 最好的选择方案是取第best_object_number:[1, 2, 3, 5, 7]个物品,total_value:2979