解读人：曲晨辉，陈盈鑫，孙楚天，杨李平，张云天

编者按

本次解读的文章是于2020年发表在INFORMS Journal on Computing的“A Lagrangian Bound on the Clique Number and an Exact Algorithm for the Maximum Edge Weight Clique Problem”。本文作者为Seyedmohammadhossein Hosseinian, Dalila B. M. M. Fontes 和 Sergiy Butenko 。​

本文探索了最大团(Maximum clique, MC)问题和最大边权团(Maximum edge weigh clique, MEWC)问题之间的联系，提出了计算团数解析上界的新思路和解决MEWC问题的精确性算法。​

本文在对MEWC问题的整数规划(Integer Programming, IP)模型进行拉格朗日松弛(Lagrangian Relaxation)得到团数解析上界之后，结合图着色问题，将团数解析上界作为上界方案，并采用了分支定界法(Branch
-and-bound, B&B)，提出了一个解决MEWC问题的精确解法。​

计算实验的结果表明，与现有方法相比，本文提出的算法具有优越的性能。

写在前面

最大团 (Maximum clique, MC)问题，即在图中找到最大团，是组合优化中最流行的问题之一。给定一个简单无向图$G=(V,E)$，其中 V = { 1 , 2 , . . . , n } V=\{1,2,...,n\} V={1,2,...,n}是顶点集，$C\subseteq V$是边集。团是顶点$C\subseteq V$推导出的一个完整的子图。如果一个团不是一个更大的团的子集，则它被称为极大团，如果图中没有更大的团，则其被称为最大团。$G$中最大团的基数则称为图的团数，用$\omega (G)$表示。

最大边权团 (Maximum edge weigh clique, MEWC)问题是最大团问题在加权图上的扩展，目的是找到图中边权和最大的团。在给定一个加权图$G=(V,E,w^E)$，每一条边 { i , j } ∈ E \{i,j\} \in E {i,j}∈E都有正权重$w_{ij}$，团的顶点$C\subseteq V$的权重和定义为$W(C)={\sum }_{(i,j)\in E(C)}{w}_{ij}$，$E(C)$是两个端点都在$C$上的边的集合。如果每条边的权重都是1，那么MEWC问题就退化成了MC问题。因此，解决MEWC问题至少和解决MC问题一样困难，是一个NP-hard问题。

本文探究了MEWC问题和MC问题之间的紧密联系。首先，本文将拉格朗日松弛 (Lagrangian Relaxation)应用于MEWC问题的整数规划模型来得到团数的解析上界。其次，结合分支定界法（Branch -and-bound, B&B）提出一种解决MEWC问题的精确算法。

最大团数上界的算法

对于图$G=(V,E,{\omega }_E)$,MEWC问题的整数规划模型如下：

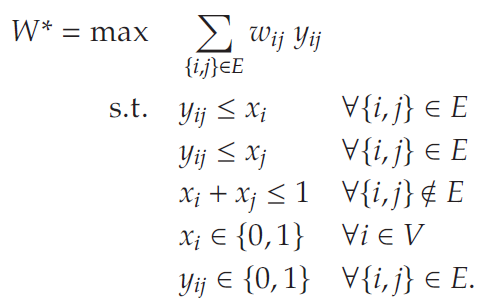
进一步的，对MEWC问题的整数规划模型进行拉格朗日松弛：

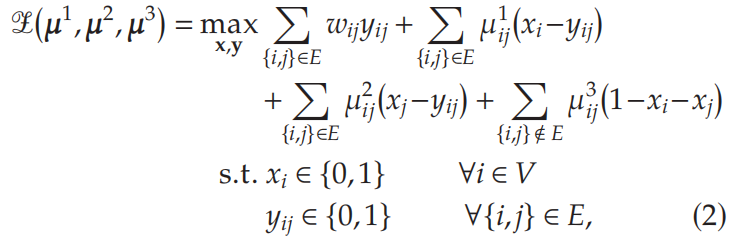
令${\mu }_{ij}^1={\mu }_{ij}^2={\mu }_{ij}^3=\mu$，得到：

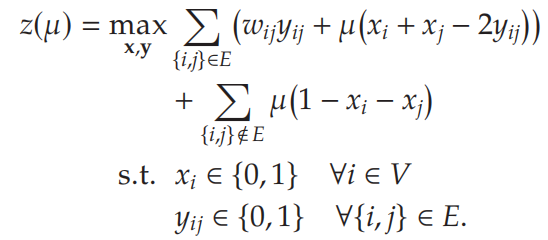
已知：

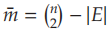
更进一步化简：

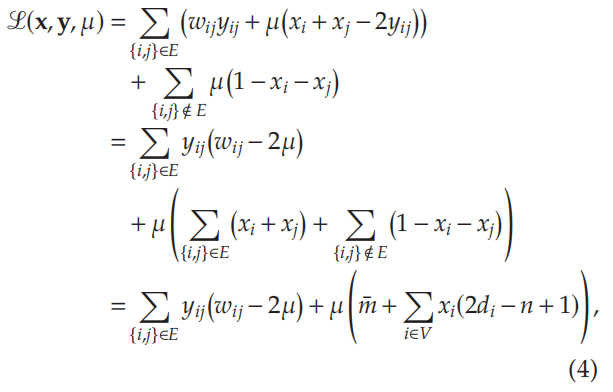
进而得到：

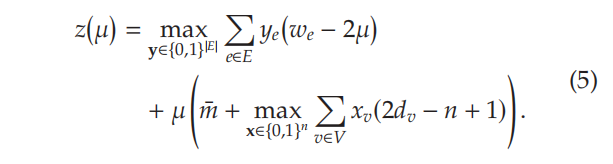
求得拉格朗日对偶的最小值，即为原问题最优值的上界：

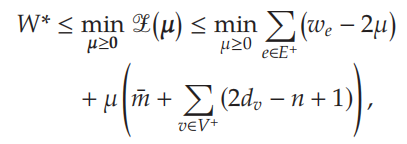
上述式子中，令$w_e=1$，即图中所有边权重为1，MEWC问题就变成了MC问题。当边权均为1时，得到MC问题的上界为：

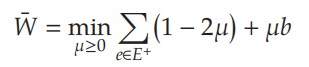
其中

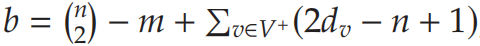
由于MC问题的最优值为 $\left(\genfrac{}{}{0ex}{}{\omega (G)}{2}\right)$，可得：

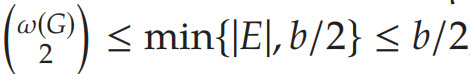
即得到最大团数的上界为：

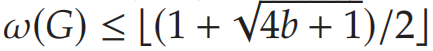
图一给出了示例：

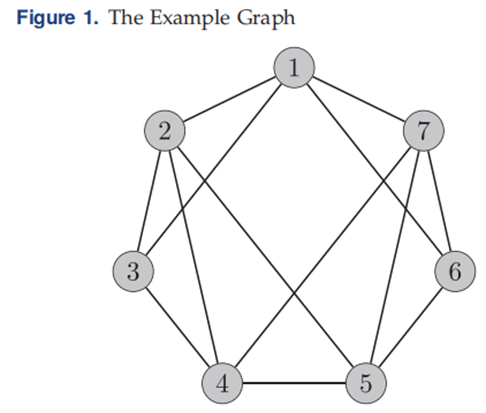
从图中可以看到，团数为3，利用本文所提团数上界计算如下，结果为4，优于Amin and Hakimi (1972)提出的可以在多项式时间内计算的团数上界（计算为5）。

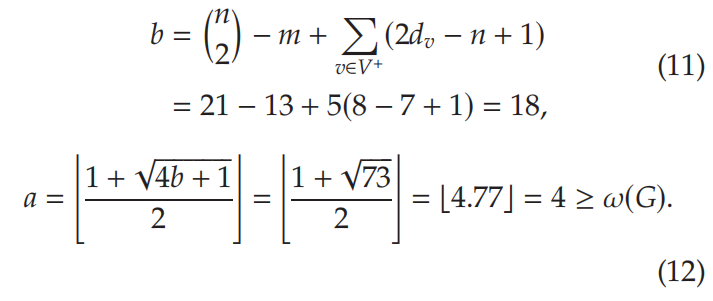
详细证明请见附录。

一种解决MEWC问题的精确算法

Upper-Bounding Method

假设$C^{\ast }$是 $G$的一个MEWC。对于$V$中的每一个顶点，令$\Gamma (i)=\{\begin{array}{lr}\frac{1}{2}{\sum }_{j\in C^{\ast }\backslash i}{w}_{ij},i\in C^{\ast }& \\ 0,i\in V\backslash C^{\ast }& \end{array}$

那么，就可以将 $W^{\ast }=W(C^{\ast })$用顶点的属性而不是边的属性来表达，即 $W(C^{\ast })={\sum }_{i\in C^{\ast }}\Gamma (i).$

可以得到 $\Gamma (i)$和 $W(C^{\ast })$的上界为$$\begin{gathered} \Gamma (i)\le \overline{\Gamma }(i)=\frac{1}{2}{\sum }_{k=1}^{\overline{w}-1}{w}_e^{(k)}:e\in {\delta }_i\forall i\in V, \\ W(C^{\ast })\le {\sum }_{k=1}^{\overline{w}}{\overline{\Gamma }}^{(k)}, \end{gathered}$$

其中 ${\delta }_i$是一个顶点 $i\in V$所附带的边的集合，上标 $(k)$表示相应集合中的第 $k$个最大值。

我们根据整个搜索过程中所访问的子图的特殊结构来细化上述方程。回顾一下，每个子图都是由现有团 $C$和它的候选列表 $L$的集合所引起的，用$G[C\cup L]$表示。考虑由 $C$的所有顶点合并成一个顶点 $v$组成的的次要部分，产生$G^{{}^{\prime }}$。在这种情况下，连接 $v$和$L$的顶点的边的权重被定义如下：$
w^{\prime}{iv}=\sum{j\in{C}}{w_{ij}},\forall i\in L.$

最终，我们可以得到如下上界，并在所提出的算法中得到了应用：$W_{G[C\cup L]}^{\ast }\le W(C)+{\sum }_{k=1}^{{\overline{w}}_L}{\overline{\Gamma }}^{\prime (k)}.$

为了计算模型中的${\overline{\omega }}_L$，选择了两种着色方法。第一个是任意图的着色数 $\chi (G)\geqq \omega (G)$。第二种方法是基于最初由Li和Quan提出的MC问题的MaxSAT编码。对于MC问题来说，第二个方法比第一个方法要更好。然而，正如我们的实验结果所示，MEWC问题并非如此，因为这两个问题使用了不同的剪枝标准，而且后一种方法中计算剪枝阈值的开销很大。

算法伪代码

本文求解框架的核心为分支定界法（Branch-and-bound, B&B），是一种用于求解混合或纯整数规划模型的精确规划算法。

分支定界法是一种搜索与迭代的方法，通过选择不同的分支变量和子问题进行搜索。具体地，把全部可行解空间反复地分割为越来越小的子集，称为分支；并且对每个子集内的解集计算一个目标下界（对于最小值问题），称为定界。在每次分支后，凡是界限超出已知最好可行解目标值的那些子集将不再进一步分支，因此许多子集可不予考虑，称为剪枝。

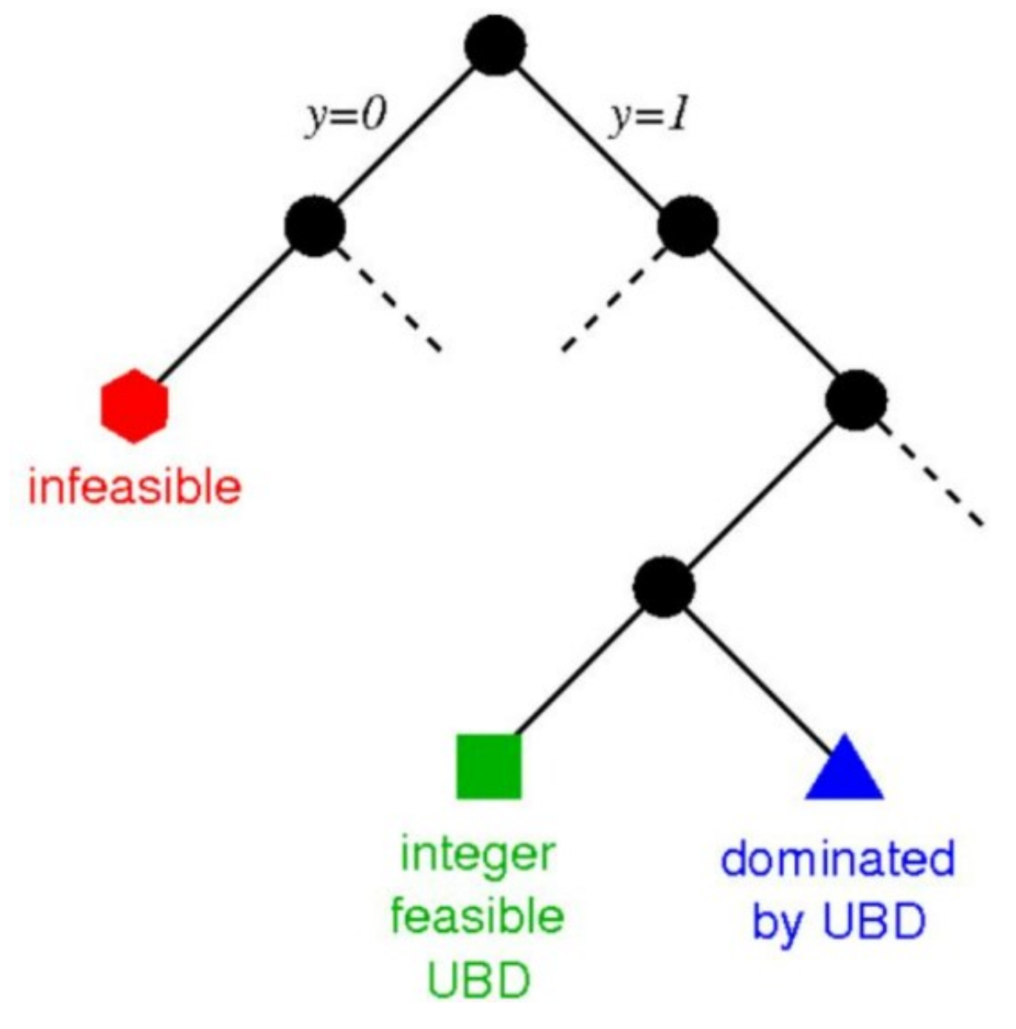
本文的求解框架如Algorithm 1所示：

Algorithm 1首先进行变量与参数的初始化。初始化当前候选团$C=\varnothing$，其权重$W=0$；最优团$C^{\ast }=\varnothing$，其权重$W^{\ast }=0$。同时，初始化与维护两个节点列表U与L，具体方法详见Appendix B的Algorithm B.1中的INITIALIZE函数。随后，调用分支定界法主函数模块BRANCH，以递归的方式展开搜索树进行寻优。BRANCH函数的所有输入参数均为全局变量，并随着搜索的进行实时更新。BRANCH函数模块具体为Algorithm 2。

Algorithm 2（即BRANCH函数模块）首先进行剪枝操作的判定，具体调用PRUNE函数。若该分支未被剪枝，则进一步分支，并将新分支出的节点加入候选集合进行分析。在调用BRANCH函数对新节点进行分析前，需要调用关键的SUBCOLOR函数生成着色的候选列表$L_v$。注意Algorithm 2第13行调用的SUBCOLOR函数，包括两种不同的实现方式，文中分别记作$SUBCOLO{R}^1$和$SUBCOLO{R}^2$。Algorithm 2以递归的方式运行，直至候选集合中再无待分析的节点，则分支定界法结束，程序回溯并输出期望的解。

关于算法伪代码的更多细节，在此不做赘述，请感兴趣的读者自行参考原文Section 3.2和Appendix。

计算实验

本节将展示各算法在DIMACS数据集（Johnson and Trick 1996）的41个基准实例的计算结果。DIMACS的实例最初是不加权的。Pullan（2008）提出了这些图的边缘加权版本，命名为DIMACS-EW。在DIMACS-EW图中，边 { i , j } ∈ E \{i,j\}∈E {i,j}∈E的权重为$w_{ij}=(i+j)mod200+1$。Table 1列出了测试实例的特征。在这个表中$|V|$，$|E|$和 "Density"分别表示图的顶点数量、边的数量和边的密度。

本文提出的所有算法都是用C++实现，用Visual C++编译，在Intel®CoreTM i7 CPU@2.90 GHz, 8 GB RAM的计算机上执行，操作系统为Windows 8.1。团数的谱上界是在同一系统上使用Intel Math Kernel Library计算得出。

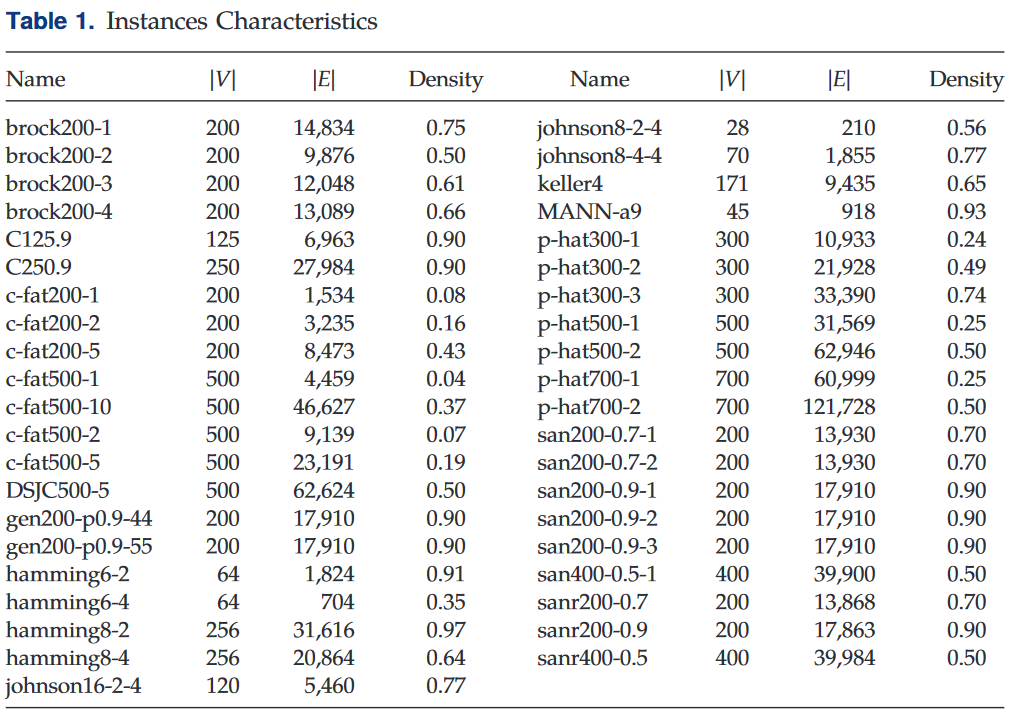
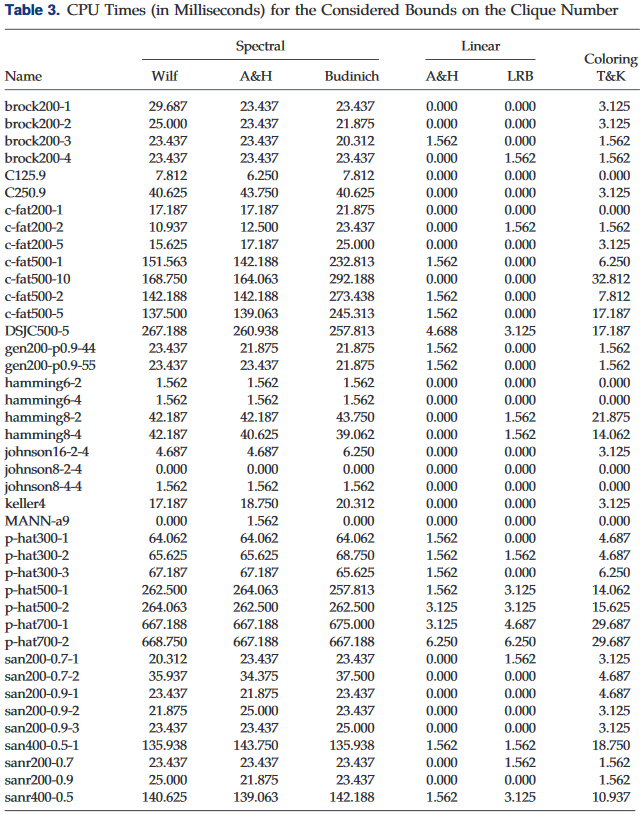
Table 2展示了关于拉格朗日松弛约束质量的结果，即Proposition 1中的a，以及文献中提出的其他分析性约束，以及Tomita和Kameda（2007）的基于着色的约束。此外，Table 3 列出了相应的CPU时间（以毫秒计）。如前所述，这些界限中有三个需要对图的邻接矩阵进行谱计算。鉴于所需计算量的不同，我将它们与Amin和Hakimi(1972)的第一个界限和本文提出的拉格朗日界限区分开来。在Table 2和Table 3中，“Wilf”、"A&H"和 "Budinich"分别指Wilf（1967）、Amin和Hakimi（1972）以及Budinich（2003）提出的界限。"LRB"一栏显示的是第2节中提出的拉格朗日松弛约束的结果。最后，"T&K"一栏报告了根据Tomita和Kameda（2007）提出的基于着色的约束的结果。

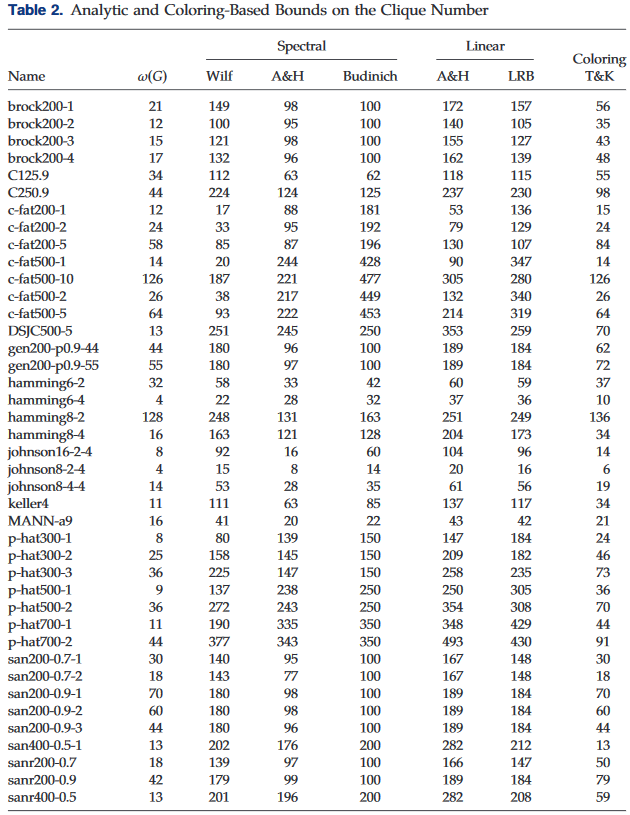
值得注意的是，除了大多涉及稀疏图形的c-fat和p-hat族之外，拉格朗日松弛约束相对接近Wilf（1967）提出的谱约束，即$\rho (A_G)+1$。除了这两个家族，拉格朗日松弛约束在所有其他图上都优于Amin和Hakimi（1972）的第一个约束，且时间复杂性相同。

接下来，将在关于MEWC问题上的表现，对本文所提出的算法、Gouveia和Martins（2015）的结果、Hosseinian等人（2018）的结果以及Shimizu等人（2019）的EWCLIQUE算法进行比较。前两项工作结果考虑了来自brock、C、c-fat、hamming、johnson、keller、MANN和p-hat族的不超过300个顶点的实例，并将解决每个实例的时间上限定为3小时。Shimizu等人（2019）报告了34个DIMACS实例的结果，时间限制为1,000秒。我们的实验涉及DIMACS-EW图的所有系列。除了所有顶点不超过300个的图之外，我们还考虑了顶点不超过700个、边缘密度不超过0.50的实例，并对每个实例使用三小时的时间限制。

Table 4总结了所记录的解决时间。在这个表中，"W*"显示了每个实例的MEWC问题的最优解值（如果知道的话）。"IP"列提供了Gouveia和Martins（2015）的结果。"CBQ"列显示了Hosseinian等人（2018）提出的算法的计算结果。"EWC"列显示的是Shimizu等人（2019）报告的EWCLIQUE算法的结果。最后两栏是关于本文提出的算法的结果。"Algorithm(1)"一栏显示了算法中使用Subcolor1函数时的求解时间，"Algorithm(2)"对应的是Subcolor2的应用。我们在表中使用了 "t-lim"来表示相应的算法在完成搜索之前由于时间限制而终止。我们用Hosseinian等人（2018）中使用的初始下限来运行我们的算法。Table 4中报告的结果包括初始下限的计算时间。

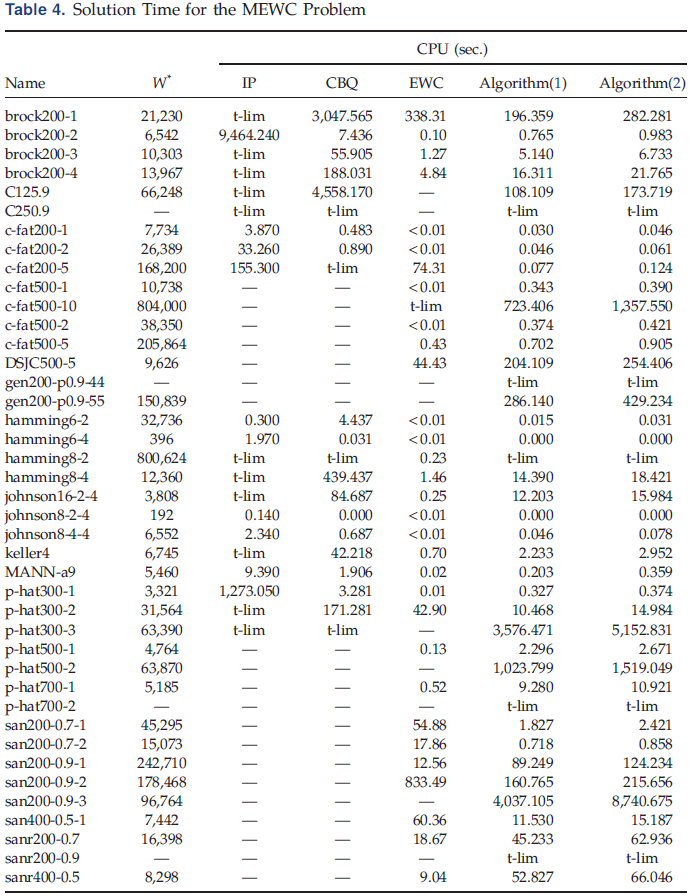
本文提出的算法（简称“本算法”）可以在三个小时内解决41个实例中的36个。本算法的求解时间比IP和CBQ获得的最佳结果要好一个数量级（除了小图）。在本算法与EWCLIQUE的比较中，两者的表现相当。然而，在两种方法都解决的30个实例中，EWCLIQUE、Algorithm(1)和Algorithm(2)解决所有这30个实例的总时间分别为1,516.54、837.866和1,122.228秒。这种差异主要源于更有挑战性的实例的解决时间。事实上，对于大多数EWCLIQUE的求解时间小于Algorithm(1)的实例，两种算法的求解时间都小于10秒。

本算法对c-fat200-5、C125.9和san族实例取得了最好的时间改进。CBQ算法未能在三个小时内解决c-fat200-5，而Gouveia和Martins（2015）的一个整数编程模型在大约155秒内解决了它，EWCLIQUE在74.31秒内解决了它。而本算法在0.077秒内解决了这个实例。Gouveia和Martins（2015）的所有九个整数编程模型都未能解决C125.9，而本算法解决这个实例的速度是CBQ算法的42倍。对于本文的方法和EWCLIQUE所涉及的san族的五个实例，Algorithm(1)解决这五个实例的总时间为264.089秒，而EWCLIQUE解决这些实例的时间为979.15秒。

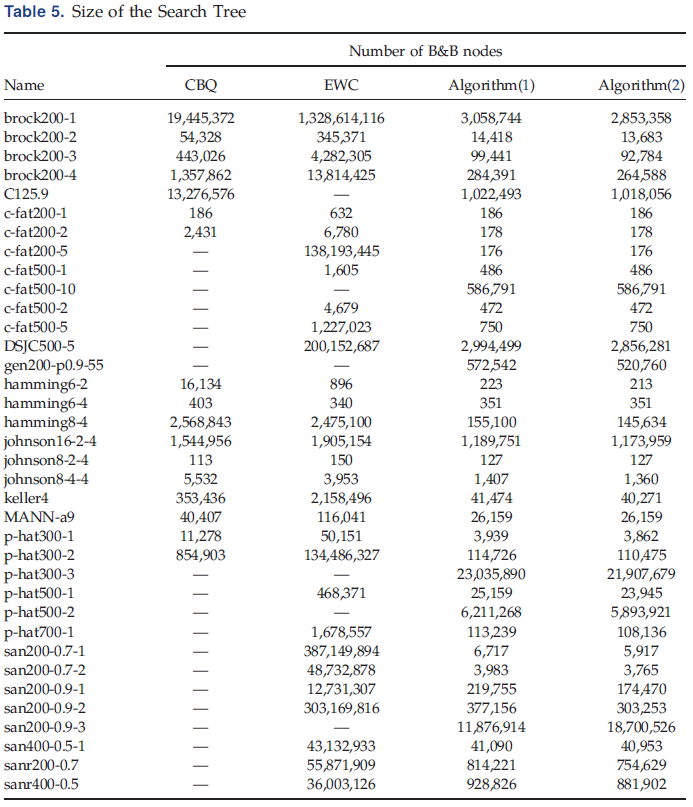
在Table 4中的五种求解方法中，有四种是组合式B&B算法，其中三种（EWC是一个例外）使用相同的初始下限和顶点排序。对于这些方法中的每一种，本文在Table 5中列出了相应搜索树的节点数，且从这个表中排除了无法解决的五个实例。可以看出，本文介绍的任何一个版本的算法中的B&B节点数都比CBQ和EWCLIQUE算法少得多，但CBQ和EWCLIQUE算法各有一个例外（Johnson8-2-4和hamming6-4）。此外，在本文的算法中，除了一个实例（san200-0.9-3）外，第二种色度方法下的B&B节点数小于（或等于）第一种方法。较好的上界预计会产生较少的B&B节点，但不能保证，因为上界的质量对B&B树的结构的影响很难预测。结合Table 4的结果，这意味着第二种色度方法产生的更好的上界（关于团数）的质量并没有弥补计算MEWC问题的剪枝阈值的开销。

参考文献

[1] 整数规划：基础、扩展及应用 (2022.06 First Edition). 殷允强，王杜娟，余玉刚.
[2]Hosseinian, S., Fontes, D. B., & Butenko, S. (2020). A lagrangian bound on the clique number and an exact algorithm for the maximum edge weight clique problem. INFORMS Journal on Computing, 32(3), 747-762.
[3] Li, C. M., & Quan, Z. (2010, July). An efficient branch-and-bound algorithm based on maxsat for the maximum clique problem. In Twenty-fourth AAAI conference on artificial intelligence.
[4] Li, C. M., & Quan, Z. (2010, October). Combining graph structure exploitation and propositional reasoning for the maximum clique problem. In 2010 22nd IEEE International Conference on Tools with Artificial Intelligence (Vol. 1, pp. 344-351). IEEE.
[5] Tomita E, Kameda T (2007) An efficient branch-and-bound algorithm for finding a maximum clique with computational experiments. J. Global Optim. 37(1):95–111.
[6] San Segundo P, Nikolaev A, Batsyn M (2015) Infra-chromatic bound for exact maximum clique search. Comput. Oper. Res. 64:293–303.