基于FPGA的Hamiton方程--辛几何算法实现（全网唯一）

news2025/7/16 10:33:21

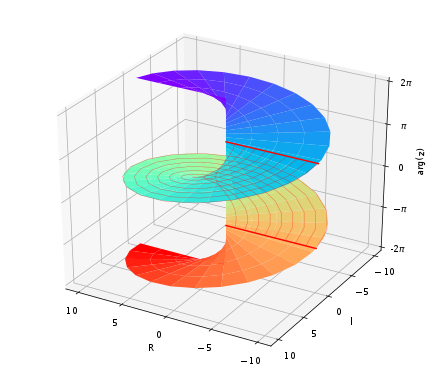
1、本文实验基于冯康院士的《哈密尔顿系统的辛几何算法》开展，链接：https://pan.baidu.com/s/1GM0Px7SLWBWzh4sXmAdcwg
提取码：fmkt

2、虽然题目写的是基于FPGA的求解，但实际上采用的是VHLS来实现的，最近根本不想写verilog算法代码。本实验做的是简单谐振子运动方程组的运算，会给出matlab代码以及相应的FPGA仿真截图。

3、Hamiton方程

3.1.谐振子Hamiton方程的一般形式

$\left\{\begin{matrix} \dot{p}=-\frac{\partial H(p,q))}{\partial q}=-\omega ^{2}q\\ \dot{q}=\frac{\partial H(p,q))}{\partial p}=p\end{matrix}\right.$

初始条件为：

$q(0)=q_{0},p(0)=p^2$

其精确解为：

$\left( {\begin{array}{*{20}{c}} {q\left( t \right)}\\ {p\left( t \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\cos \left( {\omega t} \right)}&{\frac{1}{\omega }\sin \left( {\omega t} \right)}\\ { - \omega \sin t}&{\cos \left( {\omega t} \right)} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{q_0}}\\ {{p_0}} \end{array}} \right)$

3.2 采用《哈密尔顿系统的辛几何算法》第225页的一阶差分形式展开：

由论文《Hamilton系统下基于相位误差的精细辛算法》

$\left\{ {\begin{array}{*{20}{c}} {p_i^{k + 1} = p_i^k - \tau {V_{qi}}\left( {{q^{k + 1}}} \right)}\\ {q_i^{k + 1} = q_i^k + \tau {U_{pi}}\left( {{p^k}} \right)} \end{array}} \right.\$

因此，可得：

$\left( {\begin{array}{*{20}{c}} {{q_{k + 1}}}\\ {{p_{k + 1}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1&\tau \\ { - {\omega ^2}\tau }&{1 - {\omega ^2}{\tau ^2}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{q_k}}\\ {{p_k}} \end{array}} \right)\$

采用精细化算法可得：

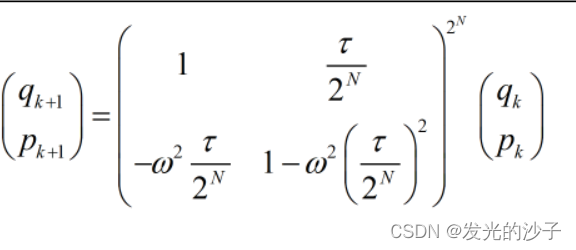
4、RK算法、一阶辛精细化算法、辛RK算法、梯形法、解析法的matlab代码

%作者：Yang Zheng
%机构：东北电力大学
%内容：对Hamilton系统的求解。 设K=4，C=R=0,M=1，则为哈密尔顿方程。于是有：dq/dt=-p;dp/dt=-4q
% RK算法
tau=0.5;
time=1000;
q0=1;
q2=0.9801;

p0=0;
p2=-0.3973;
q=zeros(ceil(time/tau),1);
p=q;
n=1;
q(n)=q0;
p(n)=p0;
A=[1 -tau/6;2*tau/3 1];
while(n<ceil(time/tau))
    B1=[q0+tau/6*(p0+2*p2);p0-2*tau/3*(q0+2*q2)];
    qp1=A\B1;
    q1=qp1(1);p1=qp1(2);
    
    B2=[q2+tau/6*(p2+2*p1);p2-2*tau/3*(q2+2*q1)];
    qp2=A\B2;
    q2=qp2(1);p2=qp2(2);
    
    %更新
    q0=q1;
    p0=p1;
    %赋值
    n=n+1;
    q(n)=q0;
    p(n)=p0;
end
plot(p,q,'r');
hold on;

% 辛1阶算法
N=10;%精细度
E=eye(2);
w=2;
B=[0 tau/2^N;-w^2*tau/2^N -w^2*(tau/2^N)^2];
%B=[w^2*(tau/2^N)^2 -w^2*tau/2^N;-tau/2^N 0];
for i = 1:N
    B=B*B+2*B;
end
M=E+B;
n=1;
q0=1;
p0=0;
q(n)=q0;
p(n)=p0;
while(n<ceil(time/tau))
    xqp=M*[q0 p0]';
    q0=xqp(1);
    p0=xqp(2);
    q(n)=q0;
    p(n)=p0;
    n=n+1;
end
plot(p,q,'y');
hold on;
% 辛RK算法
g=w*tau;
J=1/(g^4+12*g^2+144)*[g^4-60*g^2+144 12*tau*(12-g^2);-12*g*w*(12-g^2) g^4-60*g^2+144];
n=1;
q0=1;
p0=0;
q(n)=q0;
p(n)=p0;
while(n<ceil(time/tau))
    xqp=J*[q0 p0]';
    q0=xqp(1);
    p0=xqp(2);
    q(n)=q0;
    p(n)=p0;
    n=n+1;
end
plot(p,q,'k');
hold on;
%梯形法
q0=1;
p0=0;
q=zeros(ceil(time/tau),1);
p=q;
n=1;
q(n)=q0;
p(n)=p0;
A=[1 -tau/2;2*tau 1];
while(n<ceil(time/tau))
    B1=[q0+tau/2*p0;p0-2*tau*q0];
    qp1=A\B1;
    q1=qp1(1);p1=qp1(2);
    %更新
    q0=q1;
    p0=p1;
    %赋值
    n=n+1;
    q(n)=q0;
    p(n)=p0;
end
plot(p,q,'g');
hold on;
% 原方程
T=1:tau:time;
plot(-2*sin(2*T),cos(2*T),'b');

仿真结果：

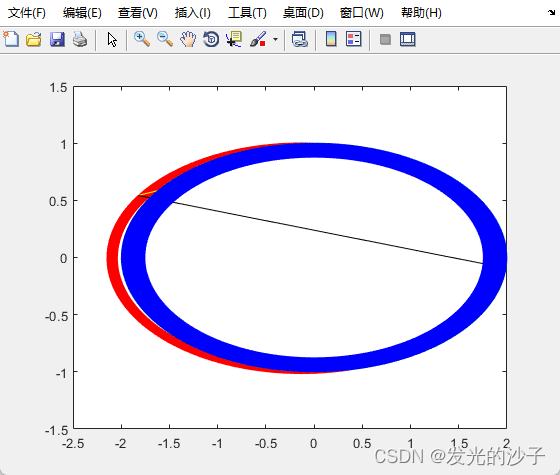
可以看到，RK法已经完全失真。

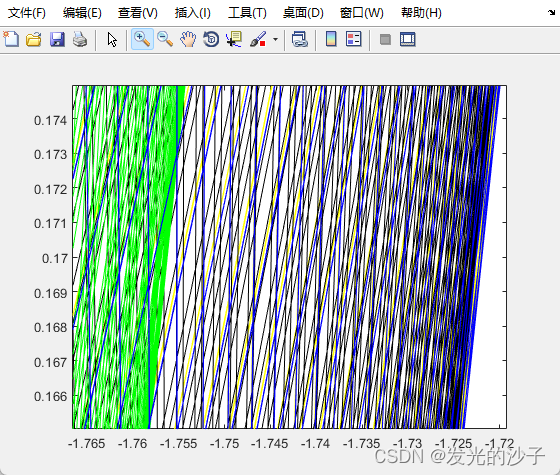
可以看到，梯形法没有长时追踪能力。一阶辛精度很高，可以追踪；辛RK没有精细化算法，但仍然可以追踪，较精细化算法误差较大。

5、基于辛RK算法的谐振子方程组求解代码

%作者：Yang Zheng
%机构：东北电力大学
%内容：对Hamilton系统的求解。 设K=[k1,k2,...,kn]，C=R=0,M=1，则为哈密尔顿方程组。K=w^2
function [q,p,q_ref,p_ref]=mul_diff_SRK(K)
    %% 辛RK
    N=length(K);
    w=sqrt(K);
    tau=0.5;
    time=1000;
    g=w*tau;
    J=zeros(2,2*N);
    for i = 1 :N
        J(:,2*i-1:2*i)=1/(g(i)^4+12*g(i)^2+144)*[g(i)^4-60*g(i)^2+144 12*tau*(12-g(i)^2);-12*g(i)*w(i)*(12-g(i)^2) g(i)^4-60*g(i)^2+144];
    end
    
    
    n=1;
    q0=ones(1,N);
    p0=zeros(1,N);
    q=zeros(ceil(time/tau),N);
    p=q;
    q(n,:)=q0;
    p(n,:)=p0;
    while(n<ceil(time/tau))
        for i = 1 :N
            xqp=J(:,2*i-1:2*i)*[q0(i) p0(i)]';
            q0(i)=xqp(1);
            p0(i)=xqp(2);
        end
        q(n,:)=q0;
        p(n,:)=p0;
        n=n+1;
    end

    %% 画出原图
    T=tau:tau:time;
    q_ref=zeros(ceil(time/tau),N);
    p_ref=zeros(ceil(time/tau),N);
    for i = 1 :N
        q_ref(:,i)=cos(w(i)*T);
        p_ref(:,i)=-w(i)*sin(w(i)*T);
    end
end

6、辛RK的vivado仿真结果，需要代码请联系作者邮箱！