使用星凸随机超曲面模型对扩展对象和分组目标进行形状跟踪（Matlab代码实现）

news2025/7/16 10:34:19

🍒🍒🍒欢迎关注🌈🌈🌈

📝个人主页：我爱Matlab

👍点赞➕评论➕收藏 == 养成习惯（一键三连）🌻🌻🌻

🍌希望大家多多支持🍓~一起加油 🤗

💬语录：将来的我一定会感谢现在奋斗的自己！

🍁🥬🕒摘要🕒🥬🍁

在传统目标跟踪技术中，早期由于传感器分辨率的限制，通常只能用点来描述目标，即目标每一时刻最多只能生成一个量测，只能对目标的质心位置、速度、加速度等进行估计。随着现代传感器技术发展，高分辨率传感器在工程中的应用越来越广泛，导致每个时刻可以得到不止一个量测，而扩展目标跟踪技术正是利用获得的多个量测信息，通过信息融合运算，得到对目标形状和运动状态的估计。

近些年扩展目标跟踪问题得到了广泛的关注，而对扩展目标形状进行估计是学者们研究的重点，因此，诞生了许多对扩展目标形状建模的方法。例如Baum等将扩展目标建模为随机超曲面模型（Random Hypersurface Model,RHM），该模型的核心思想是假设目标的量测源分布在目标边界的一个缩小版本之上，量测由处于缩小版本边界上的量测源和传感器噪声共同构成。星凸随机超曲面模型主要将径向函数用傅里叶级数展开从而描述目标轮廓，由展开系数实现对扩展目标形状建模，并结合尺度因子缩放扩展目标的形状完成对其表面量测源的建模。随机超曲面模型假设目标产生的每一量测由对应的量测源产生，这种建模方式弊端会造成量测方程具有较强的非线性。

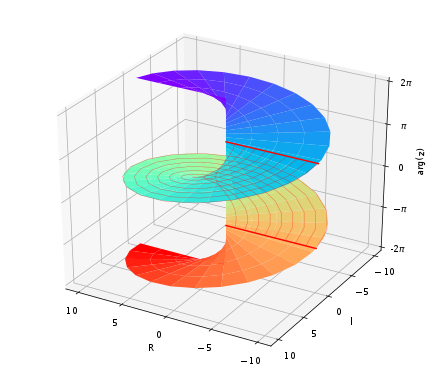
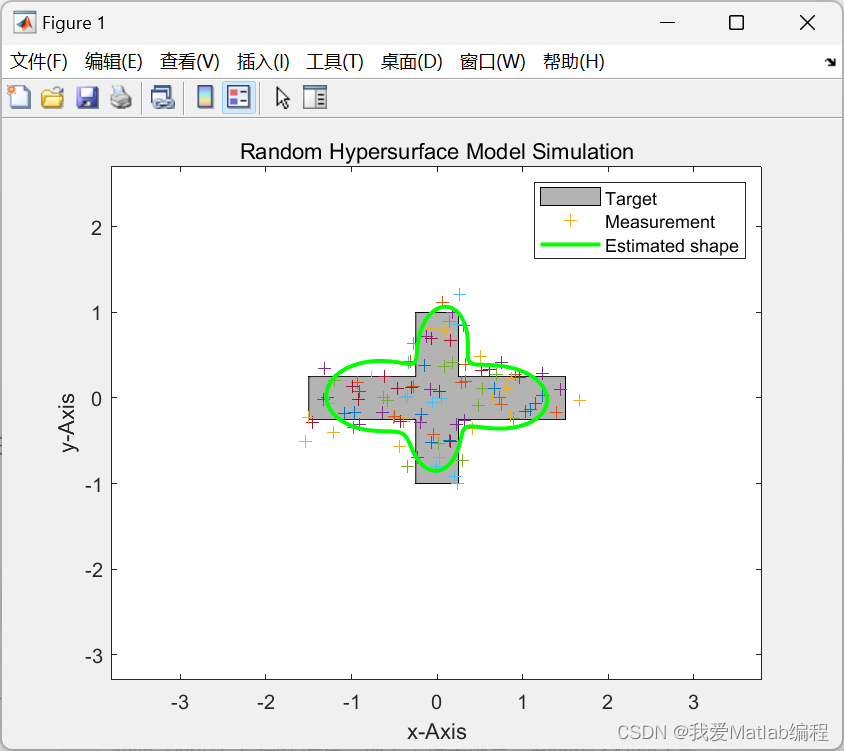
✨🔎⚡运行结果⚡🔎✨

💂♨️👨‍🎓Matlab代码👨‍🎓♨️💂

function randomHypersurfaceModel_2011(numberOfMeasurement)
if nargin ==0
numberOfMeasurement= 100;
end
% Number of Fourier coefficients
nr_Fourier_coeff = 11;

% State describtion prior [b0--bn, x, y]
x = zeros(nr_Fourier_coeff + 2, 1);
x(1) = 1.5;

% State covariance prior
C_x = diag([ones(1, nr_Fourier_coeff).*0.02, 0.3, 0.3]);

% Measurement noise
measurementNoise = diag([0.2, 0.2].^2);

% Scale properties
scale.mean = 0.7;
scale.variance = 0.08;

% Angular resolution for plotting
phi_vec = [0:0.01:2*pi];

% Object size
a = 3; % -- width of the horizontal rectangle
b = 0.5; % | height of the horizontal rectangle
c = 2; % | height of the vertical rectangle
d = 0.5; % -- width of the vertical rectangle

sizeObject = [a b c d];

% Object shape bounds
objectBounds = [[-d, -c];[d, -c];[d, -b];[a, -b];[a, b];[d, b];[d, c];
[-d, c];[-d, b];[-a, b];[-a, -b];[-d, -b]]' ./ 2;

% Main

% Plot
h_object = fill(objectBounds(1, :), objectBounds(2, :), [.7 .7 .7]);
hold on
xlim([-3 3]);
ylim([-3 3]);
axis equal
xlabel('x-Axis')
ylabel('y-Axis')
title('Random Hypersurface Model Simulation')

for j = 1 : numberOfMeasurement

% Get new measurement
newMeasurement = getNewMeasurement(sizeObject, measurementNoise);

% Filter step
[x, C_x] = UKF_FilterStep(x, C_x, newMeasurement, [scale.mean; [0 0]'], ...
blkdiag(scale.variance, measurementNoise), @f_meas_pseudo_squared, nr_Fourier_coeff);

% Plot
shape = calcShape(phi_vec, x, nr_Fourier_coeff);

h_measure = plot(newMeasurement(1), newMeasurement(2), '+');
h_shape = plot(shape(1, :), shape(2, :), 'g-', 'linewidth', 2);
legend([h_object, h_measure, h_shape],'Target', 'Measurement', 'Estimated shape')
drawnow;

if j ~= numberOfMeasurement
delete(h_shape)
end

end