区间合并计算问题
文章目录
- 区间合并计算问题
- [1326. 灌溉花园的最少水龙头数目](https://leetcode.cn/problems/minimum-number-of-taps-to-open-to-water-a-garden/)
- 贪心
- [1024. 视频拼接](https://leetcode.cn/problems/video-stitching/)
- [55. 跳跃游戏](https://leetcode.cn/problems/jump-game/)
- [45. 跳跃游戏 II](https://leetcode.cn/problems/jump-game-ii/)
- 法一:动态规划
- 法二:贪心
1326. 灌溉花园的最少水龙头数目
难度困难128
在 x 轴上有一个一维的花园。花园长度为 n,从点 0 开始,到点 n 结束。
花园里总共有 n + 1 个水龙头,分别位于 [0, 1, ..., n] 。
给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ,其中 ranges[i] (下标从 0 开始)表示:如果打开点 i 处的水龙头,可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。
请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方,请你返回 -1 。
示例 1:
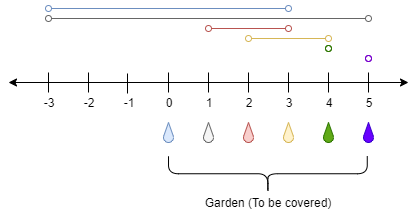
输入:n = 5, ranges = [3,4,1,1,0,0]
输出:1
解释:
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。
示例 2:
输入:n = 3, ranges = [0,0,0,0]
输出:-1
解释:即使打开所有水龙头,你也无法灌溉整个花园。
提示:
1 <= n <= 104ranges.length == n + 10 <= ranges[i] <= 100
贪心
https://leetcode.cn/problems/minimum-number-of-taps-to-open-to-water-a-garden/solution/java-tong-yong-de-yi-wei-qu-jian-jiao-bi-qfn0/
leetcode上一维的区间合并计算问题种类很多,但是大都是一个套路,起点排序,然后通过贪心的方法,进行具体分析;
这里先将水龙头位置信息转化为其有效工作区间信息;
然后根据区间的左端点进行升序;
最后枚举所有区间,通过贪心思想,获得可覆盖当前有效区间的最右区间。
class Solution {
public int minTaps(int n, int[] ranges) {
// 定义一个区间数组
int[][] region = new int[n+1][2];
// 将原来的水龙头位置信息转化为洒水区间信息
for(int i = 0; i <= n; i++){
int[] tmp = new int[2];
tmp[0] = Math.max(0, i - ranges[i]);
tmp[1] = Math.min(n, i + ranges[i]);
region[i] = tmp;
}
// 以左端点为标准进行升序
Arrays.sort(region, (a,b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
// 初始化答案,当前可用最右位置
int res = 0, right = 0;
// 初始化当前区间
int cur = 0;
// 遍历所有区间
while(cur < n+1){
// 当前区间无法覆盖到最右的有效工作范围,那么就会存在覆盖不到的间隙
if(region[cur][0] > right) break;
// 遍历可以覆盖到已经可用的最右点的下一个可用的最右边点
int rt = right;
while(cur < n+1 && region[cur][0] <= right){
rt = Math.max(rt, region[cur][1]);
cur++;
}
res++;
right = rt;
if(right == n) break;
}
return right == n ? res : -1;
}
}
0x3f:
class Solution {
public int minTaps(int n, int[] ranges) {
int[] rightMost = new int[n+1];
for(int i = 0; i <= n; i++){
int r = ranges[i];
if(i > r) rightMost[i-r] = i+r; // 对于 i-r 来说,i+r 必然是它目前的最大值
else rightMost[0] = Math.max(rightMost[0], i+r);
}
int res = 0;
int curRight = 0;
int nextRight = 0;
for(int i = 0; i < n; i++){
nextRight = Math.max(nextRight, rightMost[i]);
if(i == curRight){
// 到达已建造的桥的右端点
if(i == nextRight) return -1;// 无论怎么造桥,都无法从 i 到 i+1
curRight = nextRight;// 造一座桥
res++;
}
}
return res;
}
}
1024. 视频拼接
难度中等317
你将会获得一系列视频片段,这些片段来自于一项持续时长为 time 秒的体育赛事。这些片段可能有所重叠,也可能长度不一。
使用数组 clips 描述所有的视频片段,其中 clips[i] = [starti, endi] 表示:某个视频片段开始于 starti 并于 endi 结束。
甚至可以对这些片段自由地再剪辑:
- 例如,片段
[0, 7]可以剪切成[0, 1] + [1, 3] + [3, 7]三部分。
我们需要将这些片段进行再剪辑,并将剪辑后的内容拼接成覆盖整个运动过程的片段([0, time])。返回所需片段的最小数目,如果无法完成该任务,则返回 -1 。
示例 1:
输入:clips = [[0,2],[4,6],[8,10],[1,9],[1,5],[5,9]], time = 10
输出:3
解释:
选中 [0,2], [8,10], [1,9] 这三个片段。
然后,按下面的方案重制比赛片段:
将 [1,9] 再剪辑为 [1,2] + [2,8] + [8,9] 。
现在手上的片段为 [0,2] + [2,8] + [8,10],而这些覆盖了整场比赛 [0, 10]。
示例 2:
输入:clips = [[0,1],[1,2]], time = 5
输出:-1
解释:
无法只用 [0,1] 和 [1,2] 覆盖 [0,5] 的整个过程。
示例 3:
输入:clips = [[0,1],[6,8],[0,2],[5,6],[0,4],[0,3],[6,7],[1,3],[4,7],[1,4],[2,5],[2,6],[3,4],[4,5],[5,7],[6,9]], time = 9
输出:3
解释:
选取片段 [0,4], [4,7] 和 [6,9] 。
提示:
1 <= clips.length <= 1000 <= starti <= endi <= 1001 <= time <= 100
class Solution {
public int videoStitching(int[][] clips, int time) {
Arrays.sort(clips, (a,b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
int right = 0, cur = 0;
int res = 0;
while(cur < clips.length){
if(clips[cur][0] > right) return -1;
int rt = right;
while(cur < clips.length && clips[cur][0] <= right){
rt = Math.max(rt,clips[cur][1]);
cur++;
}
res++;
right = rt;
if(right >= time) break;
}
return right >= time ? res : -1;
}
}
55. 跳跃游戏
难度中等2204
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
1 <= nums.length <= 3 * 1040 <= nums[i] <= 105
class Solution {
public boolean canJump(int[] nums) {
int n = nums.length;
if(n == 1) return true;
int right = 0;
int cur = 0;
while(cur < n && right < n-1){
if(right < cur) break; // 怎么走都无法越过cur
right = Math.max(right, cur + nums[cur]);
cur++;
}
if(right < n-1) return false;
else return true;
}
}
45. 跳跃游戏 II
难度中等1966
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示:
1 <= nums.length <= 1040 <= nums[i] <= 1000- 题目保证可以到达
nums[n-1]
法一:动态规划
class Solution {
public int jump(int[] nums) {
int n = nums.length;
int[] dp = new int[n+1];
Arrays.fill(dp, (int)1e5);
dp[0] = 0;
for(int i = 0; i < n; i++){
for(int j = i+1; j <= Math.min(n, i+nums[i]); j++){
dp[j] = Math.min(dp[j], dp[i] + 1);
}
}
return dp[n-1];
}
}
法二:贪心
如果我们「贪心」地进行正向查找,每次找到可到达的最远位置,就可以在线性时间内得到最少的跳跃次数。
在具体的实现中,我们维护当前能够到达的最大下标位置,记为边界。我们从左到右遍历数组,到达边界时,更新边界并将跳跃次数增加 1。
class Solution {
public int jump(int[] nums) {
int n = nums.length;
int end = 0;
int maxPosition = 0;
int steps = 0;
for(int i = 0; i < length-1; i++){
maxPosition = Math.max(maxPosition, i + nums[i]);
if(i == end){
end = maxPosition;
steps++;
}
}
return steps;
}
}
![[JavaEE系列] 详解面试中HTTP协议HTTPS协议](https://img-blog.csdnimg.cn/715d87c897b243ea9defae554c40835d.png)