LeetCode 513找树左下角的值 112路径总和113路径总和ii 106从中序与后序遍历序列构造二叉树

文章目录

- - - 513找树左下角的值
    - - c++ 代码实现
      - python 代码实现
    - 112路径总和
    - - c++ 代码实现
      - python 代码实现
    - 113路径总和ii
    - - c++代码实现
      - python 代码实现
    - 106从中序与后序遍历序列构造二叉树
    - - c++代码实现
      - python 代码实现

513找树左下角的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

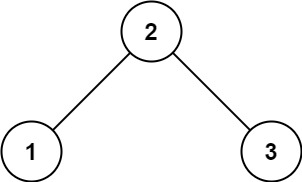
输入: root = [2,1,3]
输出: 1

示例 2:

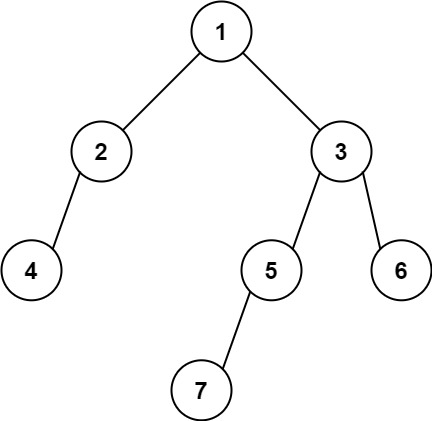
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

提示:

二叉树的节点个数的范围是 [1,104]
-231 <= Node.val <= 231 - 1

c++ 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // maxDepth用来记录最大深度，result记录最大深度最左节点的数值。
    int maxDepth = -1;
    int result = 0;
    void leftVal(TreeNode * node, int depth) {
        if (node->left == nullptr && node->right == nullptr) {
            // 最底层：最大深度。
            if (depth > maxDepth) {
                maxDepth = depth;
                result = node->val;
            }
            return;
        }

        if (node->left) {
            leftVal(node->left, depth + 1);     // depth + 1 隐藏了回溯
        }
        if (node->right) {
            leftVal(node->right, depth + 1);    // 隐藏了回溯
        }
    }
    int findBottomLeftValue(TreeNode* root) {
        leftVal(root, 0);
        return result;
    }
};

python 代码实现

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.max_depth = -1
        self.result = 0

    def leftVal(self, node, depth):
        # 停止条件
        if not node.left and not node.right:
            if depth > self.max_depth:
                self.max_depth = depth
                self.result = node.val
        
        # 单次遍历
        if node.left:
            self.leftVal(node.left, depth + 1)
        if node.right:
            self.leftVal(node.right, depth + 1)

    def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
        self.leftVal(root, 0)
        return self.result

112路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

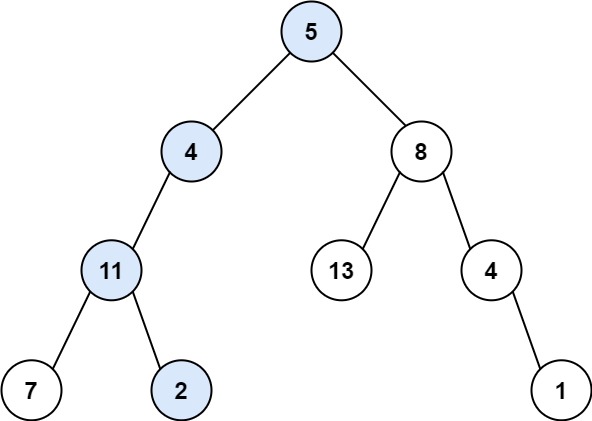
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

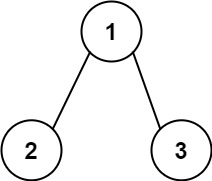
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

c++ 代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 递归三部曲
    bool pathSum(TreeNode * root, int count) {
        // 停止条件, 两边都为空时，已经到节点末尾
        if (root->left == nullptr && root->right == nullptr && count == 0) {
            return true;    
        }
        if (root->left == nullptr && root->right == nullptr) {
            return false;
        }

        if (root->left) {
            count -= root->left->val;   // 计算
            if (pathSum(root->left, count)) {
                return true;
            }
            count += root->left->val;   // 回溯
        }

        if (root->right) {
            count -= root->right->val;
            if (pathSum(root->right, count)){
                return true;
            }
            count += root->right->val;
        }

        return false;
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        if (root == nullptr) return false;
        return pathSum(root, targetSum - root->val);
    }
};

python 代码实现

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def pathSum(self, root, count):
        if not root.left and not root.right and count == 0:
            return True
        if not root.left and not root.right:
            return False
        
        if root.left:
            count -= root.left.val
            if self.pathSum(root.left, count):
                return True
            count += root.left.val
        
        if root.right:
            count -= root.right.val
            if self.pathSum(root.right, count):
                return True
            count += root.right.val

        return False

    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
        if not root: return False
        return self.pathSum(root, targetSum - root.val)

113路径总和ii

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

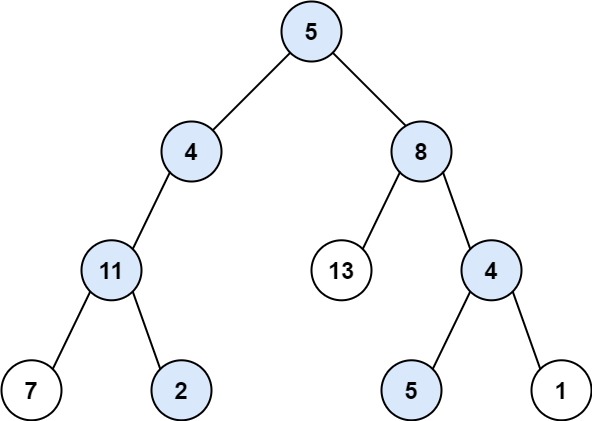
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

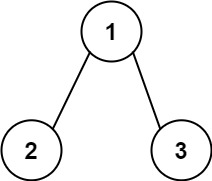
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

提示：

树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

c++代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    
    void resultSum(TreeNode * root, int count) {
        if (root->left == nullptr && root->right == nullptr && count == 0) {
            result.push_back(path);
            return;
        }
        if (root->left == nullptr && root->right == nullptr) {
            return;
        }

        if (root->left) {
            path.push_back(root->left->val);
            count -= root->left->val;
            resultSum(root->left, count);
            count += root->left->val;
            path.pop_back();
        }

        if (root->right) {
            path.push_back(root->right->val);
            count -= root->right->val;
            resultSum(root->right, count);
            count += root->right->val;
            path.pop_back();
        }
    }

    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        if (root == nullptr) {
            return result;
        }
        path.push_back(root->val);
        resultSum(root, targetSum - root->val);
        return result;
    }
};

python 代码实现

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.result = []
        self.path = []

    def resultSum(self, root, count):
        if not root.left and not root.right and count == 0:
            self.result.append(self.path[:])
            return 
        
        if not root.left and not root.right:
            return

        if root.left:
            self.path.append(root.left.val)
            count -= root.left.val
            self.resultSum(root.left, count)
            count += root.left.val
            self.path.remove(root.left.val)
        
        if root.right:
            self.path.append(root.right.val)
            count -= root.right.val
            self.resultSum(root.right, count)
            count += root.right.val
            self.path.remove(root.right.val)

    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
        if not root:
            return self.result
        self.path.append(root.val)
        self.resultSum(root, targetSum - root.val)
        return self.result

106从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

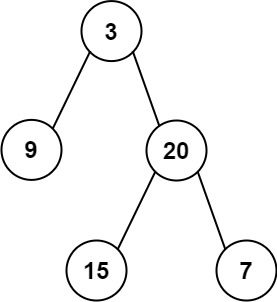
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由不同的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历
第一步：如果数组大小为零的话，说明是空节点了。
第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
第四步：切割中序数组，切成中序左数组和中序右数组（顺序别搞反了，一定是先切中序数组）
第五步：切割后序数组，切成后序左数组和后序右数组
第六步：递归处理左区间和右区间

c++代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:

    TreeNode* help(vector<int>& inorder, vector<int>& postorder) {
        // 后序是否为空
        if (postorder.size() == 0) return nullptr;

        // 后序遍历数组最后一个元素，就是当前的中间节点
        int rootVal = postorder[postorder.size() - 1];
        TreeNode * node = new TreeNode(rootVal);

        // 叶子节点
        if (postorder.size() == 1) return node;

        // 找到中序遍历的切割点
        int index;
        for (index = 0; index < inorder.size(); index++){
            if (inorder[index] == rootVal) break;
        }

        // 切割中序数组
        vector<int> leftInorder(inorder.begin(), inorder.begin() + index);
        // +1 中序的根节点，直接删除了，不需要
        vector<int> rightInorder(inorder.begin() + index + 1, inorder.end());

        // 删除，舍弃后序末尾
        postorder.resize(postorder.size() - 1);

        // 切割后序数组
        // 已上面左中序数组的大小，为切割点，中序和后序数组大小一致。
        vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
        vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());

        // 递归处理左区间，右区间
        node->left = help(leftInorder, leftPostorder);
        node->right = help(rightInorder, rightPostorder);

        return node;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if (inorder.size() == 0 || postorder.size() == 0){
            return nullptr;
        }
        return help(inorder, postorder);
    }
};

python 代码实现

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def help(self, inorder, postorder):
        # 后序是否为空
        if len(postorder) == 0:
            return None
        
        # 后序遍历数组最后一个元素，就是当前的中间节点
        rootVal = postorder[len(postorder) - 1]
        node = TreeNode(rootVal)
        
        # 叶子节点
        if len(postorder) == 1:
             return node

        # 找到中序遍历的切割点
        index = 0
        for i in range(len(inorder)):
            if inorder[i] == rootVal:
                index = i
                break        

        # 切割中序数组
        leftInorder = inorder[:index]
        rightInorder = inorder[index+1:]

        # 删除，舍弃后序末尾
        postorder.pop()

        # 切割后序数组
        leftPostorder = postorder[:len(leftInorder)]
        rightPostorder = postorder[len(leftInorder):]

        # 递归处理左区间，右区间
        node.left = self.help(leftInorder, leftPostorder)
        node.right = self.help(rightInorder, rightPostorder)

        return node
    def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
        if len(inorder) == 0 or len(postorder) == 0:
            return None
        return self.help(inorder, postorder)