图论算法大合集【包括图的dfs和bfs遍历】【欧拉回路】【判断连通图】【Dijkstra算法】【floyd算法】【最小生成树prim算法】【拓扑排序】

图论算法大合集

- 一. dfs和bfs 过程中要有visited数组标记已遍历过的节点
- - - 6-1.1 邻接矩阵存储图的深度优先遍历
    - 6-1.2 邻接表存储图的广度优先遍历
- 二、欧拉回路（度为偶数，且为连通图）
- - - 6-1.3 哥尼斯堡的“七桥问题”
- 三、判断连通图
- - - 6-1.4 地下迷宫探索
- 四、Dijkstra算法
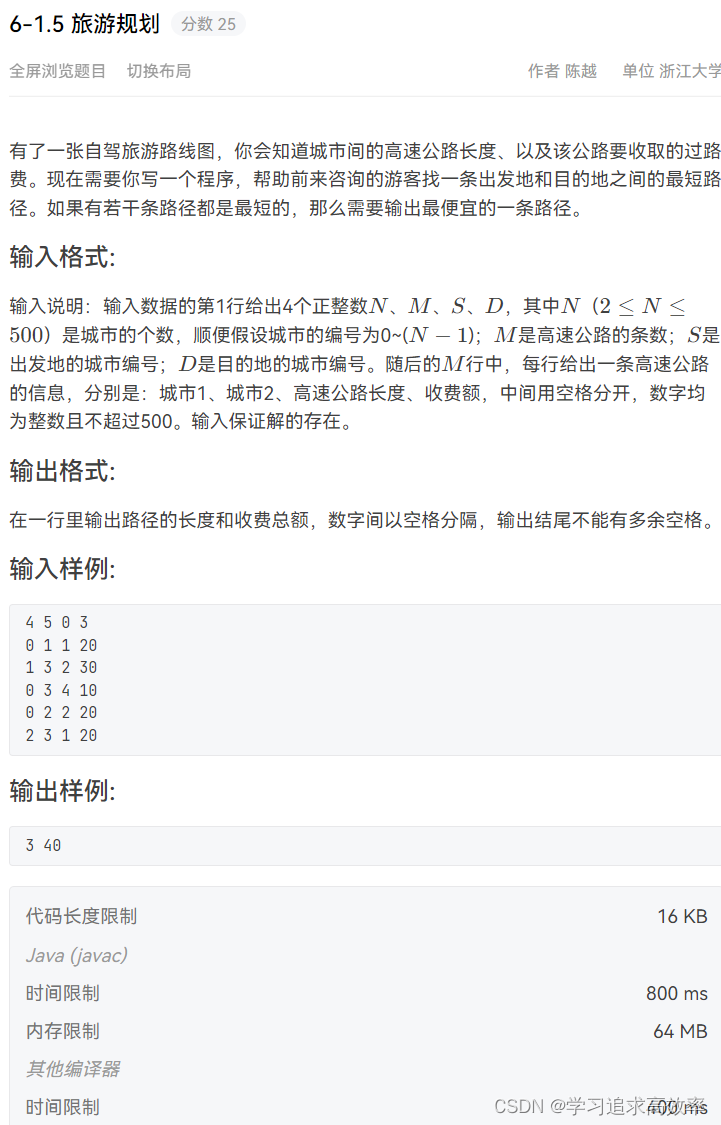
- - - 6-1.5 旅游规划
- 五、floyd算法
- - - 案例6-1.6 哈利·波特的考试
- 六、最小生存树【prim】(博客)
- - - 案例6-1.7 公路村村通 (30 分)
- 七、BFS和DFS的遍历区别
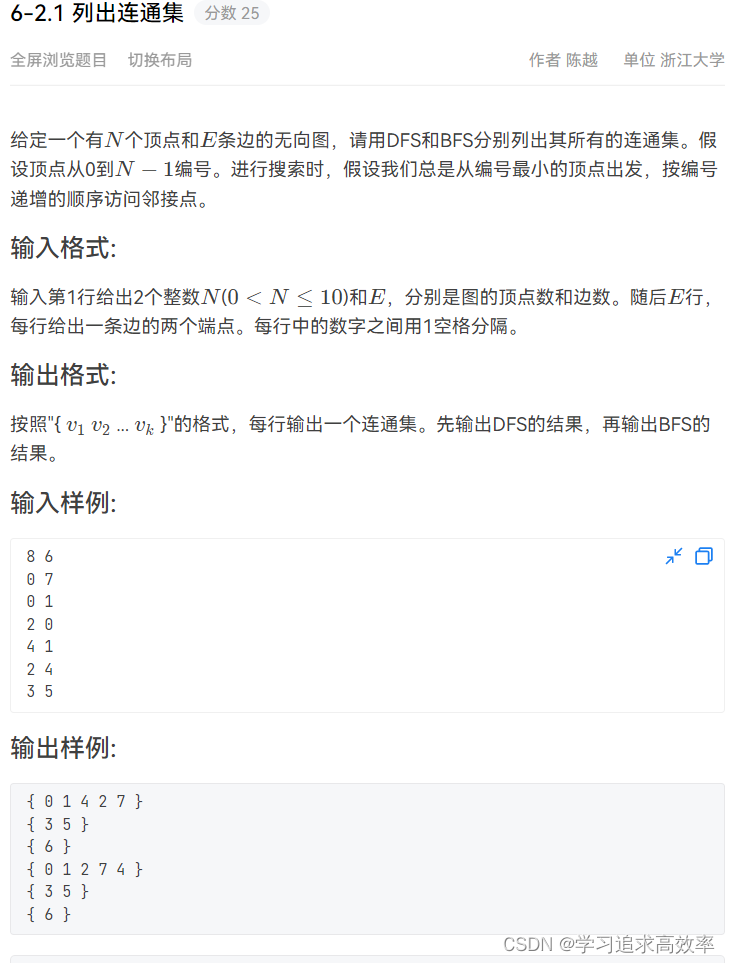
- - - 6-2.1 列出连通集
- 八、走迷宫或走荷叶，需要dfs（博客）
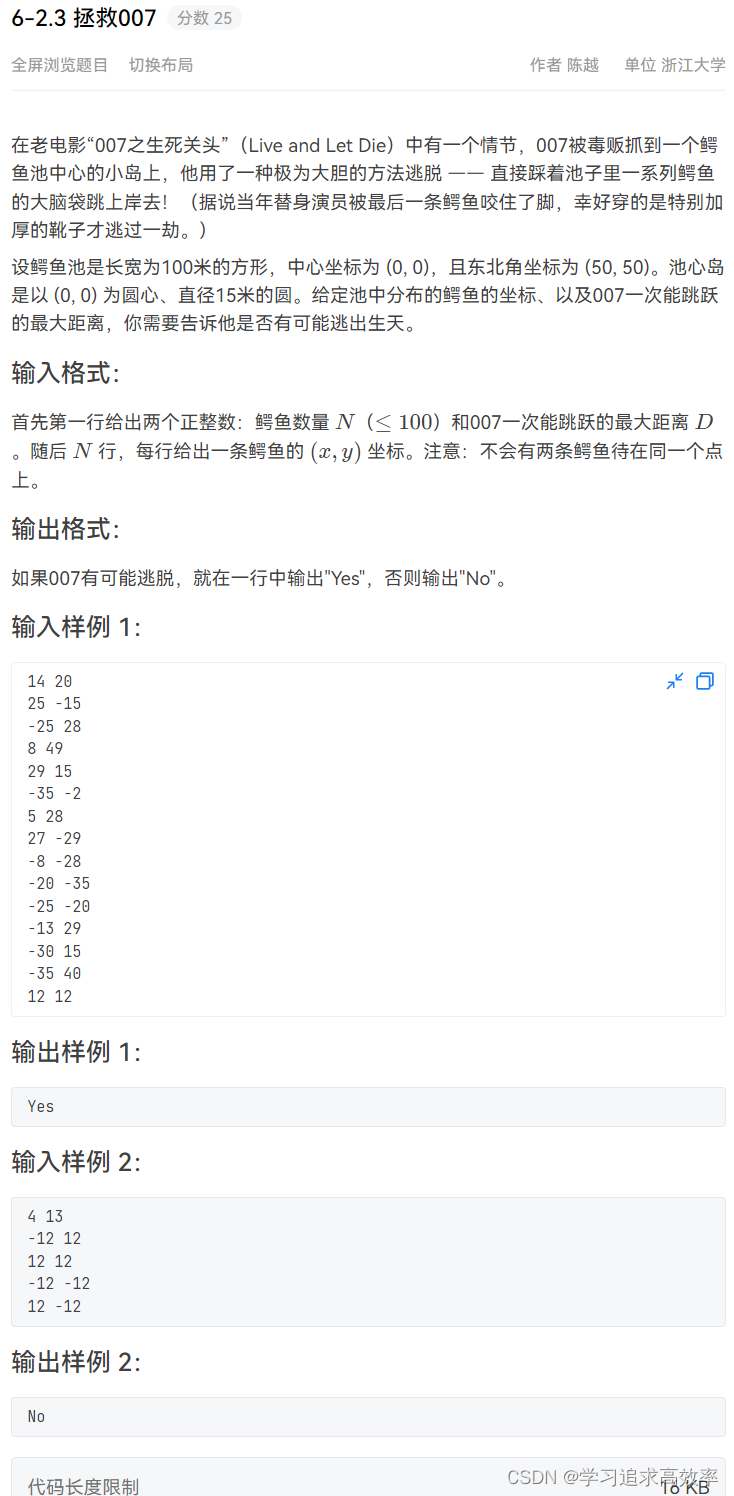
- - - 6-2.3 拯救007
- 九、拓扑排序（博客）
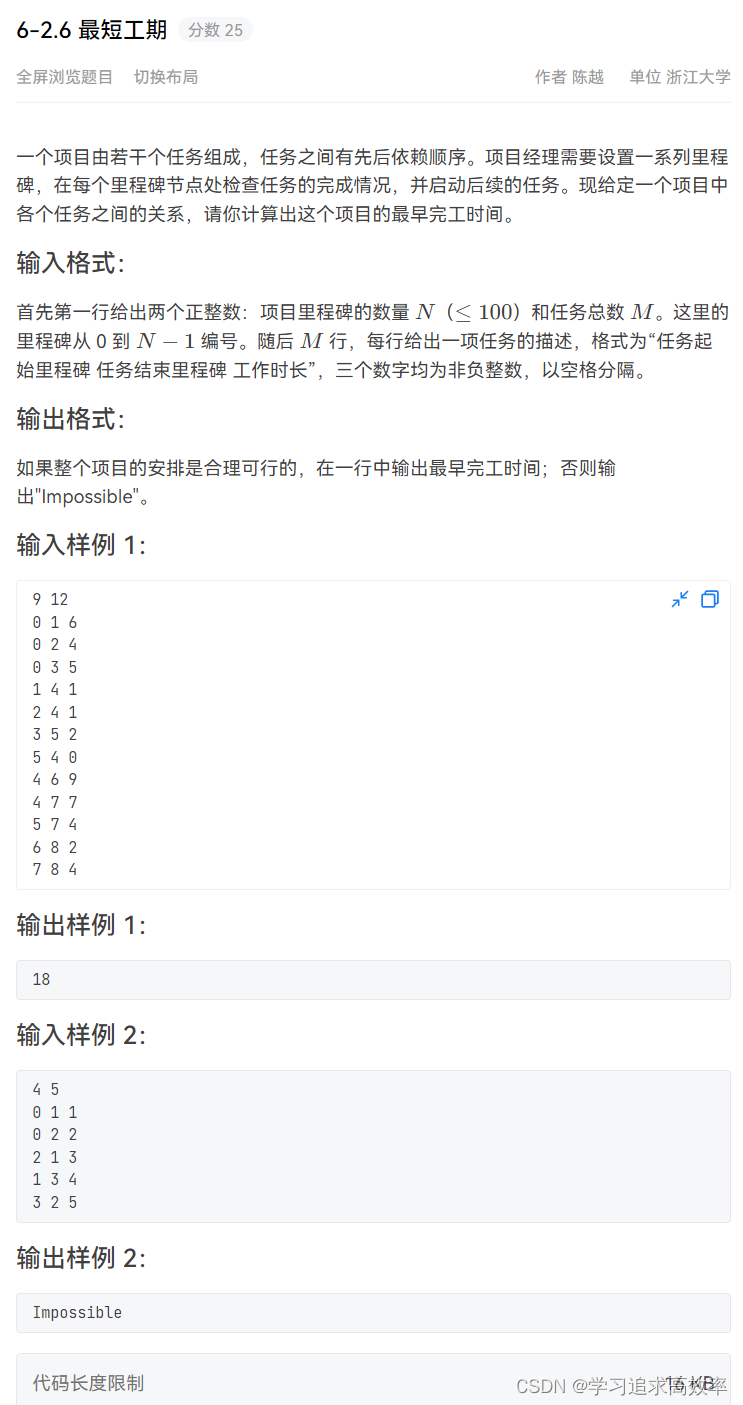
- - - 6-2.6 最短工期

一. dfs和bfs 过程中要有visited数组标记已遍历过的节点

6-1.1 邻接矩阵存储图的深度优先遍历

在这里插入图片描述

void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) )
{
    Visited[V]=true;//先标记顶点被访问
    Visit(V);//访问顶点的邻接点
    for(int i=0;i<Graph->Nv;i++)
    {
        //遍历顶点的邻接点
        if(Graph->G[V][i]==1&&!(Visited[i]))
            DFS(Graph,i,Visit);//如果邻接点可达并且没有被访问过，那么以邻接点为顶点再次进行深度优先遍历
    }
    return;
}

6-1.2 邻接表存储图的广度优先遍历

在这里插入图片描述

void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) )
{
    PtrToAdjVNode p;//边表头指针
    PtrToAdjVNode queue[MaxVertexNum];
    int head=0;
    int tail=0;//定义队列
    Visit(S);
    Visited[S]=true;//标记
    
    queue[tail++]=Graph->G[S].FirstEdge;//将与顶点相连的边表头指针入队
    while(head!=tail)
    {//遍历整个队列
        p=queue[head++];
            while(p!=NULL)
            {
                if(Visited[p->AdjV]==false){//如果没有被访问过
                    queue[tail++]=Graph->G[p->AdjV].FirstEdge;//入队
                    Visit(p->AdjV);
                    Visited[p->AdjV]=true;
                }
                p=p->Next;
            }
    }
}

二、欧拉回路（度为偶数，且为连通图）

6-1.3 哥尼斯堡的“七桥问题”

在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;
//用全局变量会自动初始化，相当方便喔！
int g[1001][1001];//邻接矩阵储存图
int visited[1001];//访问过了的节点记为1
int du[1001];//记录每个节点的度
int n, m;
 
//最基本的dfs板子
void dfs(int v0) {
	visited[v0] = 1;
	for (int i = 1; i <= n; i++)
		if (visited[i] == 0 && g[v0][i] != 0)
			dfs(i);
}
 
int main() {
	cin >> n >> m;
	int a, b;
	for (int i = 0; i < m; i++) {
		cin >> a >> b;
		g[a][b] = g[b][a] = 1;
		//题目是无向图，相应节点的度加加
		du[a]++;
		du[b]++;
	}
	for (int i = 1; i <= n; i++) {
		//只要有一个节点的度为奇数，就不能存在欧拉回路，直接输出就行！
		if (du[i] % 2 != 0) {
			cout << 0;
			return 0;
		}
	}
	//满足了上面还要保证图连通，dfs和bfs求图连通都可以
	dfs(1);
	//遍历节点，看是否全部标记完
	for (int i = 1; i <= n; i++) {
		if (visited[i] == 0) {
			cout << 0;
			return 0;
		}
	}
	cout << 1;
	return 0;
}

三、判断连通图

6-1.4 地下迷宫探索

在这里插入图片描述

#include<iostream>
#include<string>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
int f[1005][1005] , book[1005] , a[1005];
int n , m , s;
int tip = 0;
void dfs(int k)
{
    //a[++tip] = k;
    book[k] = 1;
    for(int i = 1 ; i <= n ; i++ )
    {
        if(f[k][i] == 1 && book[i] == 0)
        {
            cout<<" "<<i;
            dfs(i);
            cout<<" "<<k;
        }
    }
}
int main()
{
    int flag = 1;
    int x , y;
    cin>>n>>m>>s;
    for(int i = 1 ; i <= m ; i++)
    {
        cin>>x>>y;
        f[x][y] = 1;f[y][x] = 1;
    }
    cout<<s;
    dfs(s);
    for(int i = 1 ; i <= n ; i++)
    {
        if(book[i] == 0)
        {
            flag = 0;
            break;
        }
    }
    if(flag == 0)
        cout<<" 0";
}

四、Dijkstra算法

6-1.5 旅游规划

在这里插入图片描述

#include<stdio.h>
#include<stdlib.h>

#define MAXVEX 505
#define INFINITY  65535

void CreateGraph( );
void Dijkstra( int v);


int G[MAXVEX][MAXVEX][2];//定义三维数组
int Num_vertex,Num_edge;
int final[MAXVEX];        //final[]=1表示求得最短路径
int distance[MAXVEX];   //表示求的最短距离
int pay[MAXVEX];       //表示最少费用

int main()
{
    int s,d;
    scanf("%d %d %d %d",&Num_vertex,&Num_edge,&s,&d);
    CreateGraph();
    Dijkstra(s);
    if( distance[d]<INFINITY ){
        printf("%d %d",distance[d],pay[d]);
    }

    return 0;
}

void CreateGraph()
{
    //用邻接矩阵表示图
    int i,j;
    int v1,v2;
    int distance,fee;  //dn表示距离，f表示费用

    for( i=0; i<Num_vertex; i++)
    {
        for( j=0; j<Num_vertex; j++)
        {
            G[i][j][0] = INFINITY;  //初始化
            G[i][j][1] = INFINITY;
        }
    }

    for( i=0; i<Num_edge; i++)  //注意这里是读入边
    {
        scanf("%d %d %d %d",&v1,&v2,&distance,&fee);
        G[v1][v2][0] = G[v2][v1][0]=distance;
        G[v1][v2][1] = G[v2][v1][1]=fee;
    }
}

void Dijkstra( int v)
{
    //求从v结点到其他各结点的最短距离
    int i,j,k;
    int min,cost;
    /*初始化阶段*/
    for( i=0; i<Num_vertex; i++)
    {
        final[i] =0;
        distance[i] =G[v][i][0];   //将与v点有连接的结点加上距离
        pay[i] =G[v][i][1];
    }
    final[v] = 1;
    distance[v] =0;   //V到V距离为0
    pay[v] = 0;

    /*主循环阶段*/
    for( i=1; i<Num_vertex; i++)
    {
        min = INFINITY;     //当前所知离v结点的最近距离
        for( j=0; j<Num_vertex; j++)
        {
            //寻找离v结点的最近距离
            if( !final[j] && distance[j]<min)
            {
                k = j;
                min = distance[j];
                cost = pay[j];
            }
        }

        final[k] = 1;
        for( j=0; j<Num_vertex; j++)
        {
            //修正最短路径和距离
            if( !final[j] && (min+G[k][j][0]<distance[j]))
            {
                distance[j] = min+G[k][j][0];
                pay[j] = cost + G[k][j][1];

            }
            else if( !final[j] && (min+G[k][j][0]==distance[j]) && (cost+G[k][j][1] < pay[j]))
            {

                pay[j] = cost + G[k][j][1];
            }
        }
    }
}

五、floyd算法

案例6-1.6 哈利·波特的考试

在这里插入图片描述

#include<iostream>
#define INT 0x3f3f3f3f
using namespace std;
int main()
{
    int a,b,c[110][110],e,f,g,h,i,j,k,min=INT,max,n;
    for(e=0;e<110;e++)//设初值
        for(f=0;f<110;f++)
        {
            if(e==f)//初值自己变自己就是零喽
                c[e][f]=0;
            else
                c[e][f]=INT;
        }
    cin>>a>>b;
    while(b--)
    {
        cin>>e>>f>>g;
        c[e][f]=c[f][e]=g;
    }
    for(k=1;k<=a;k++)//floyd算法
        for(i=1;i<=a;i++)
            for(j=1;j<=a;j++)
            {
                if(c[i][j]>c[i][k]+c[k][j])
                    c[i][j]=c[i][k]+c[k][j];
            }
    for(i=1;i<=a;i++)//行最高就是选该动物要变所有动物的最小花费
    {
        max=0;
        for(j=1;j<=a;j++)
        {
            if(max<c[i][j])
                max=c[i][j];
        }
        if(min>max)//比较选哪个动物咒语最短
        {
            n=i;
            min=max;
        }
    }
    if(min==INT)//如果min==TNT就说明无论选个动物都存在无法变的动物喽
        cout<<"0"<<endl;
    else
    cout<<n<<' '<<min<<endl;
}

六、最小生存树【prim】(博客)

博客链接
从1开始找到1连接的最短路径点A，然后再从点A找除已经连接的点的最短路径，以此类推。

案例6-1.7 公路村村通 (30 分)

在这里插入图片描述

#include<iostream>
#include<cstring>
using namespace std;
const int inf=0x3f3f3f3f;
const int maxn=1010;
int map[maxn][maxn];
int vis[maxn],dis[maxn];
int n,m;
int prim()
{
	memset(dis,inf,sizeof(dis));
	int sum=0;
	for(int i=0;i<n;++i)
	{
		int t=-1;
		for(int j=1;j<=n;++j)
		{
			if(vis[j]==0&&(t==-1||dis[j]<dis[t]))
				t=j;
		}
		if(i&&dis[t]==inf)
			return inf;
		if(i)
			sum+=dis[t];
		vis[t]=1;
		for(int j=1;j<=n;++j)
			dis[j]=min(dis[j],map[t][j]);
	}
	return sum;	 
}
int main()
{
	int x,y,z;
	cin>>n>>m;
	memset(map,inf,sizeof(map));
	for(int i=1;i<=n;++i)
		map[i][i]=0;
	while(m--)
	{
		cin>>x>>y>>z;
		map[x][y]=map[y][x]=min(map[x][y],z);
	}
	int sum=prim();
	if(sum==inf)
		cout<<-1;
	else
		cout<<sum;
	return 0;
}

七、BFS和DFS的遍历区别

6-2.1 列出连通集

在这里插入图片描述

#include <stdio.h>
#include <stdlib.h>
#define Max 11

int A[Max][Max]={0},B[Max]={0},Q[Max]={0};

int E,N,head = -1,rear = -1;

void DFS(int );

void BFS(int );

void Enqueue(int );

int Dequeue();

int main()
{
	int i,x,y;
	scanf("%d %d",&N,&E);
	for(i=0; i<E; i++){
		scanf("%d %d",&x,&y);
		A[x][y] = 1;
	}
	for(i=0; i<N; i++){
		if(!B[i]){
			printf("{");
			DFS(i);
			printf("}\n");
		}
	}
	for(i=0; i<N; i++)
		B[i] = 0;
	for(i=0; i<N; i++){
		if(!B[i]){
			printf("{");
			BFS(i);
			printf("}\n");
		}
	}
}

void DFS(int v)
{
	int i;
	B[v] = 1;
	printf("%d ",v);
	for(i=v; i<N; i++)
		if(!B[i]&&(A[v][i]||A[i][v]))
			DFS(i);
}

void BFS(int v)
{
	int i;
	B[v] = 1;
	printf("%d ",v);
	Enqueue(v);
	while(head!=rear){
		v = Dequeue();
		for(i=v; i<N; i++)
			if(!B[i]&&(A[v][i]||A[i][v])){
				B[i] = 1;
				printf("%d ",i);
				Enqueue(i);
			}
	}
}

void Enqueue(int i)
{
	Q[++rear] = i;
}

int Dequeue()
{
	return Q[++head];
}

八、走迷宫或走荷叶，需要dfs（博客）

博客链接

6-2.3 拯救007

在这里插入图片描述

#include<iostream>
#include<cmath>
using namespace std;
//1.判断是否能直接从岛上跳到岸上：D+7.5>=50
//2.从岛上跳到一个鳄鱼头上 （第一步）： D+7.5>=sqrt(x*x+y*y)
//3.由一个鳄鱼头A跳到另一个鳄鱼头B：(x2-x1)*(x2-x1)+(y2-y1)*(y2-y1)<=D*D
//4.判断目前所在的鳄鱼头是否能直接跳到岸上：D>=50-|x|或者D>=50-|y|
//5.每一次跳到鳄鱼头上都要标记为走过了
int N,D,vis[101]={0},a,b;
struct Point{
	int x,y;
}; 
Point point[101];
int jump(int i,int j)	//判断是否能从i跳到j 
{
	int x1=point[i].x;
	int y1=point[i].y;
	int x2=point[j].x;
	int y2=point[j].y; 
	if((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1)<=D*D)
		return 1;
	else return 0;	
}
int firstjump(int i)	//判断是否能从岛上直接跳到第i个位置 
{
	int x=point[i].x;
	int y=point[i].y;
	if((D+7.5)*(D+7.5)>=x*x+y*y)
	{
		return 1;
	}else return 0;
}
int canleave(int i)		//判断是否能从这个点跳回岸边 
{
	int x=point[i].x;
	int y=point[i].y;
	if(D>=50-abs(x)||D>=50-abs(y))
	{
		return 1;
	}
	else return 0;
}
int DFS(int i)
{
	int answer=0;
	vis[i]=1;
	if(canleave(i))
	{
		answer=1;
	}else {
		//如果从这个点不能跳回岸边，那我就继续找 
		for(int j=0;j<N;j++)
		{
			if(!vis[j]&&jump(i,j))		//如果没有被访问过 并且可以从这个点跳过去就DFS 
			{
				answer=DFS(j);
				if(answer==1)
				break;
			}
		}
	}
	return answer;
}
int main()
{
	cin>>N>>D;
	for(int i=0;i<N;i++)
	{
		cin>>a>>b;
		point[i].x=a;
		point[i].y=b;
	}
	if(D>=42.5)        //直接从岛上跳到岸上
	{
		cout<<"Yes";
		return 0;
	}
	int answer;
	for(int i=0;i<N;i++)
	{
		if(vis[i]==0&&firstjump(i))
		{
			answer=DFS(i);
			if(answer==1)break;
		}
	}
	if(answer==1)cout<<"Yes";
		else cout<<"No";
}

九、拓扑排序（博客）

6-2.6 最短工期

博客链接
在这里插入图片描述

#include<iostream>
#include<queue>
using namespace std;
int main()
{
    queue<int>l;
    int a,b,c[101][101],d[101]={0},e[101]={0},f,g,h,i,j,ma,ans=0;
// c数组用来存储节点，
/*d数组用来记录完成每个节点的最大时间（只有时间最大，
才能保证该节点的所有节点都完成）并且是最大时间，
不是时间之和*/
//e数组用来记录每个节点的入读数
    for(f=0;f<101;f++)
        for(g=0;g<101;g++)
            c[f][g]=-1;
    cin>>a>>b;
    while(b--)
    {
        cin>>f>>g>>h;
        c[f][g]=h;
        e[g]++;
    }
// 1. 把系列一入队列
    for(f=0;f<a;f++)
        if(e[f]==0)
        {
            ans++;
            l.push(f);
            e[f]=-1;
        }
// 2. 取出队头，遍历连接点，比较两个最大值（走到该节点的最大值，最短时间的最大值）
// 3. 遍历一个节点，入读--如果为0了，入队列
    while(!l.empty())
    {
        f=l.front();
        l.pop();
        for(g=0;g<a;g++)
        {
            if(c[f][g]!=-1&&e[g]>0)
            {
                e[g]--;
                d[g]=max(d[g],d[f]+c[f][g]);
                ma=max(ma,d[g]);
                if(e[g]==0)
                {
                    l.push(g);
                    e[g]=-1;
                    ans++;
                }
            }
        }
    }
//*****最后需要注意的一点,判断是否为有环图
    if(ans!=a)
        cout<<"Impossible"<<endl;
    else
        cout<<ma<<endl;
}