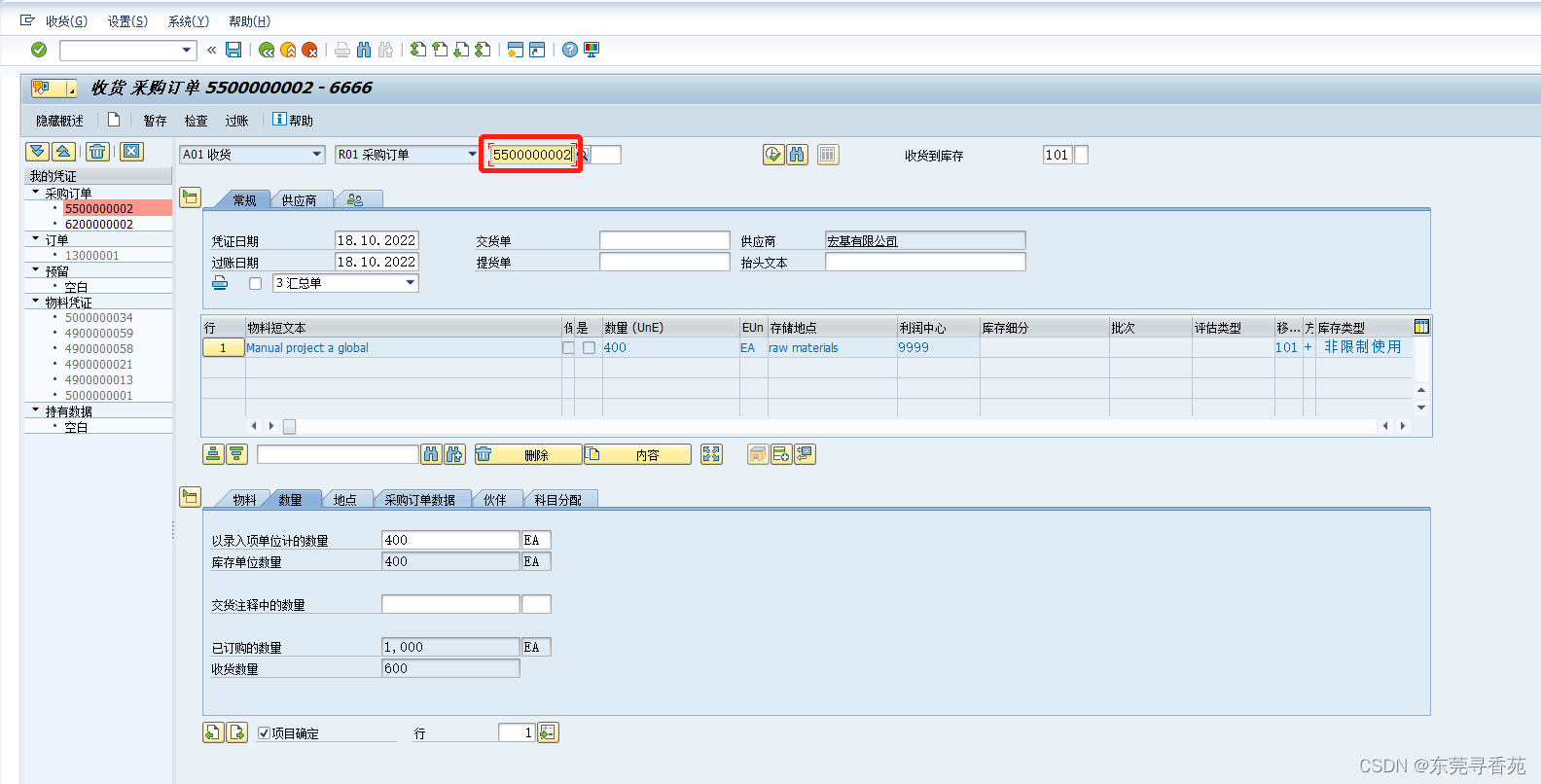
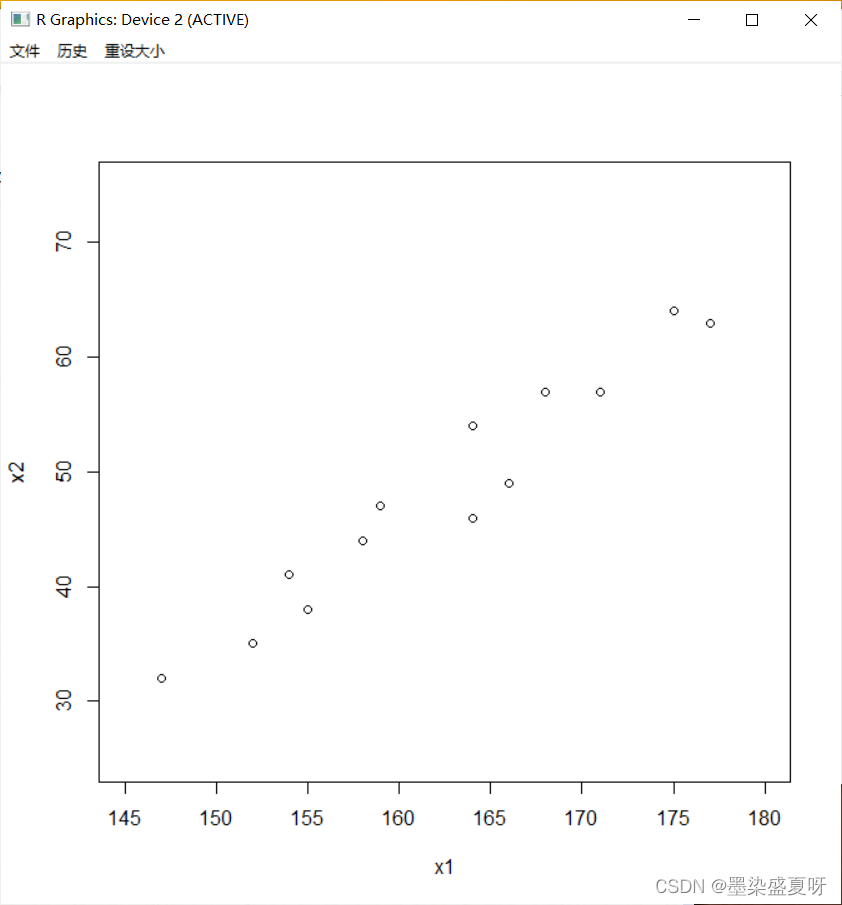
例8.1：今有14名学生的身高和体重数据，做相关图以显示相关变量间的关系。

x1=c(147,171,175,159,155,152,158,154,164,168,166,159,164,177) 

x2=c(32,57,64,1,38,35,44,41,54,57,49,47,46,63)

plot(x1,x2,xlim = c(145,180),ylim=c(25,75))

出错：

lines(c(146,178),c(30,66),lwd=2)

lines(c(163,166),c(54,47))

library(shape)

解决方法如下：

1.安装该包：install.packages("shape")

library(shape);

lines(getellipse(24,3,mid=c(162,48),angle = 48),lty=3)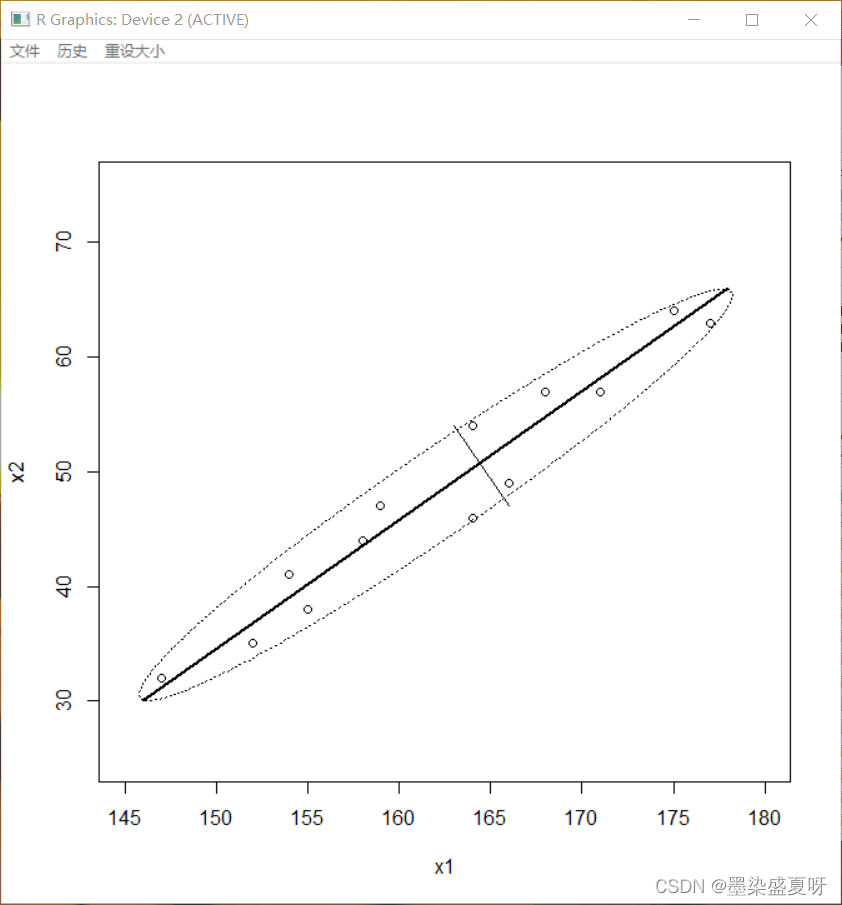

        正如二维椭圆有两个主轴,三维桶球有三个主轴一样,有几个变量,就有几个主成分。当然，选择越少的主成分,降维就越好。那么,什么是标准呢?那就是这些被选的主成分所代表的主轴的长度之和占了主轴长度总和的大部分。有些学者建议,所选的主轴总长度占所有主轴长度之和的80%左右即可,其实,这只是一个大体的说法;具体选几个,要根据实际情况而定。但如果所有涉及的变量都不那么相关,就很难降维。

X=data.frame(x1,x2) S=cov(X);S #协方差阵

x1 x2 x1 77.45604 95.31868 x2 95.31868 257.36264

R=cor(X);R #相关系数阵

x1 x2 x1 1.0000000 0.6751148 x2 0.6751148 1.0000000

主成分的性质：

主成分分析函数

princomp(x,cor = FAL.SE,scores = TRUE,-…)

princomp(X,cor = FALSE,scores = TRUE) #主成分分析函数

x为数据矩阵或数据框;

cor表示是否用相关系数阵,默认为协方差阵;scores表示是否输出成分得分

pc=princomp(X);pc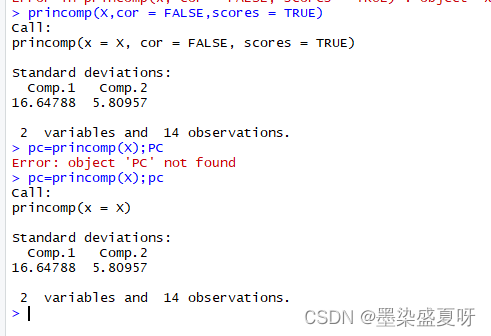

names(pc) #主成分的对象

[1] "sdev" "loadings" "center" "scale" "n.obs" "scores" "call"

pc $ sdev^2 #主成分方差

Comp.1 Comp.2 277.15195 33.75111